【LeetCode Solutions】LeetCode 热题 100 题解(16 ~ 20)
CONTENTS
- 普通数组 - LeetCode 238. 除自身以外数组的乘积(中等)
- 普通数组 - LeetCode 41. 缺失的第一个正数(困难)
- 矩阵 - LeetCode 73. 矩阵置零(中等)
- 矩阵 - LeetCode 54. 螺旋矩阵(中等)
- 矩阵 - LeetCode 48. 旋转图像(中等)
普通数组 - LeetCode 238. 除自身以外数组的乘积(中等)
【题目描述】
给你一个整数数组 nums,返回数组 answer,其中 answer[i] 等于 nums 中除 nums[i] 之外其余各元素的乘积。
题目数据保证数组 nums 之中任意元素的全部前缀元素和后缀的乘积都在 32 位整数范围内。
请不要使用除法,且在 O(n)O(n)O(n) 时间复杂度内完成此题。
【示例 1】
输入: nums = [1,2,3,4]
输出: [24,12,8,6]
【示例 2】
输入: nums = [-1,1,0,-3,3]
输出: [0,0,9,0,0]
【提示】
2<=nums.length<=1052 <= nums.length <= 10^52<=nums.length<=105
−30<=nums[i]<=30-30 <= nums[i] <= 30−30<=nums[i]<=30
输入保证数组 answer[i] 在 32 位整数范围内
进阶:你可以在 O(1)O(1)O(1) 的额外空间复杂度内完成这个题目吗?(出于对空间复杂度分析的目的,输出数组不被视为额外空间)
【分析】
本题是前缀和的思想,不考虑空间要求的情况下我们可以预处理出两个数组 p[i]p[i]p[i] 和 s[i]s[i]s[i] 分别表示 iii 之前所有数的乘积(nums[0]∗nums[1]∗⋯∗nums[i−1]nums[0] * nums[1] * \dots * nums[i - 1]nums[0]∗nums[1]∗⋯∗nums[i−1])以及 iii 之后所有数的乘积(nums[i+1]∗nums[i+2]∗⋯∗nums[n−1]nums[i + 1] * nums[i + 2] * \dots * nums[n - 1]nums[i+1]∗nums[i+2]∗⋯∗nums[n−1])。
题目要求我们只能开一个额外的答案数组,那么我们可以将数组 sss 省去,先在输出数组中预处理出前缀乘积 ppp,然后我们再倒序遍历数组,遍历的过程中用一个变量记录当前的后缀乘积即可。
【代码】
class Solution {
public:vector<int> productExceptSelf(vector<int>& nums) {int n = nums.size();vector<int> res(n);res[0] = 1; // 边界初始化for (int i = 1; i < n; i++)res[i] = res[i - 1] * nums[i - 1]; // res[i] 表示 [0, i - 1] 区间中所有元素的乘积for (int i = n - 1, mul = 1; ~i; i--)res[i] *= mul, mul *= nums[i]; // mul 表示 [i + 1, n - 1] 区间中所有元素的乘积return res;}
};
普通数组 - LeetCode 41. 缺失的第一个正数(困难)
【题目描述】
给你一个未排序的整数数组 nums,请你找出其中没有出现的最小的正整数。
请你实现时间复杂度为 O(n)O(n)O(n) 并且只使用常数级别额外空间的解决方案。
【示例 1】
输入:nums = [1,2,0]
输出:3
【示例 2】
输入:nums = [3,4,-1,1]
输出:2
【示例 3】
输入:nums = [7,8,9,11,12]
输出:1
【提示】
1≤nums.length≤5∗1051\le nums.length\le 5 * 10^51≤nums.length≤5∗105
−231≤nums[i]≤231−1-2^{31}\le nums[i]\le 2^{31} - 1−231≤nums[i]≤231−1
【分析】
注意本题的时空复杂度,不能用排序以及哈希表之类的做法。
我们可以用置换的方法求解,我们记 nnn 为 numsnumsnums 的长度,因此答案一定在 1∼n+11\sim n+11∼n+1 之间(因为最完美的情况是 numnumnum 中有 1∼n1\sim n1∼n)。
我们利用两两交换的方法将 numnumnum 中在 1∼n1\sim n1∼n 范围内的数放置到其对应的位置上,也就是 nums[i] = i + 1。但其中有若干个位置上的数是错误的,每一个错误的位置就代表了一个缺失的正数。以 [3, 4, -1, 1] 为例,置换后的数组应当为 [1, -1, 3, 4],我们就可以知道缺失的数为 222。
注意在交换的过程中应判断两数是否相等防止死循环。
【代码】
class Solution {
public:int firstMissingPositive(vector<int>& nums) {int n = nums.size();for (int i = 0; i < n; i++)// 将当前数置换到其对应的位置 num[i] - 1while (nums[i] > 0 && nums[i] <= n && nums[i] != nums[nums[i] - 1])swap(nums[i], nums[nums[i] - 1]);for (int i = 0; i < n; i++)if (nums[i] != i + 1) return i + 1; // 该位置上没有对应的正整数说明缺失了return n + 1; // 1 ~ n 全部没有缺失}
};
矩阵 - LeetCode 73. 矩阵置零(中等)
【题目描述】
给定一个 m x n 的矩阵,如果一个元素为 0,则将其所在行和列的所有元素都设为 0。请使用原地算法。
【示例 1】
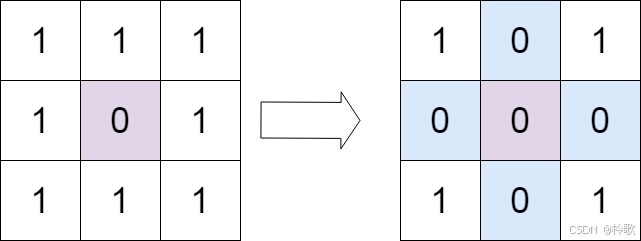
输入:matrix = [[1,1,1],[1,0,1],[1,1,1]]
输出:[[1,0,1],[0,0,0],[1,0,1]]
【示例 2】
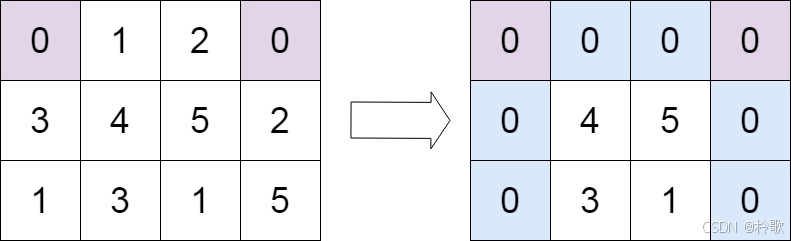
输入:matrix = [[0,1,2,0],[3,4,5,2],[1,3,1,5]]
输出:[[0,0,0,0],[0,4,5,0],[0,3,1,0]]
【提示】
m==matrix.lengthm == matrix.lengthm==matrix.length
n==matrix[0].lengthn == matrix[0].lengthn==matrix[0].length
1≤m,n≤2001\le m, n\le2001≤m,n≤200
−231≤matrix[i][j]≤231−1-2^{31}\le matrix[i][j]\le 2^{31}-1−231≤matrix[i][j]≤231−1
【分析】
我们需要用原矩阵的第一行来记录每一列是否有 0,用第一列来记录每一行是否有 0。但是第一行与第一列是否有 0 的信息无法保存,因此还需要使用两个额外的变量来记录第一行与第一列是否有 0。
【代码】
class Solution {
public:void setZeroes(vector<vector<int>>& g) {bool r0 = false, c0 = false; // 第一行或者第一列是否有 0for (int i = 0; i < g[0].size(); i++) // 判断第一行是否有 0if (!g[0][i]) { r0 = true; break; }for (int i = 0; i < g.size(); i++) // 判断第一列是否有 0if (!g[i][0]) { c0 = true; break; }for (int i = 1; i < g.size(); i++) // 判断其余行是否有 0for (int j = 1; j < g[0].size(); j++)if (!g[i][j]) { g[i][0] = 0; break; }for (int i = 1; i < g[0].size(); i++) // 判断其余列是否有 0for (int j = 1; j < g.size(); j++)if (!g[j][i]) { g[0][i] = 0; break; }for (int i = 1; i < g[0].size(); i++) // 遍历第一行,将为 0 的元素所在的列置零if (!g[0][i])for (int j = 1; j < g.size(); j++)g[j][i] = 0;for (int i = 1; i < g.size(); i++) // 遍历第一列,将为 0 的元素所在的行置零if (!g[i][0])for (int j = 1; j < g[0].size(); j++)g[i][j] = 0;if (r0) for (int i = 0; i < g[0].size(); i++) g[0][i] = 0; // 第一行置零if (c0) for (int i = 0; i < g.size(); i++) g[i][0] = 0; // 第一列置零}
};
矩阵 - LeetCode 54. 螺旋矩阵(中等)
【题目描述】
给你一个 m 行 n 列的矩阵 matrix,请按照顺时针螺旋顺序,返回矩阵中的所有元素。
【示例 1】
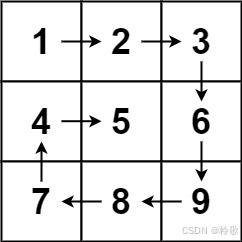
输入:matrix = [[1,2,3],[4,5,6],[7,8,9]]
输出:[1,2,3,6,9,8,7,4,5]
【示例 2】
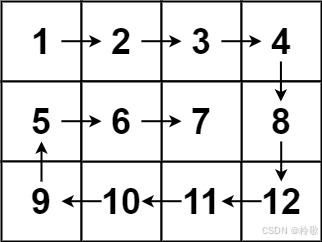
输入:matrix = [[1,2,3,4],[5,6,7,8],[9,10,11,12]]
输出:[1,2,3,4,8,12,11,10,9,5,6,7]
【提示】
m==matrix.lengthm == matrix.lengthm==matrix.length
n==matrix[i].lengthn == matrix[i].lengthn==matrix[i].length
1≤m,n≤101\le m, n\le 101≤m,n≤10
−100≤matrix[i][j]≤100-100\le matrix[i][j]\le 100−100≤matrix[i][j]≤100
【分析】
分别设置向右、向下、向左、向上四个方向向量,然后模拟一遍即可,走出界或是已经遍历过了改变一下方向即可。
【代码】
class Solution {
public:vector<int> spiralOrder(vector<vector<int>>& matrix) {int n = matrix.size(), m = matrix[0].size();int dx[] = { 0, 1, 0, -1 }, dy[] = { 1, 0, -1, 0 }; // 分别表示右、下、左、上的方向向量vector<int> res;for (int i = 0, x = 0, y = 0, d = 0; i < n * m; i++) { // 总共遍历 n * m 个点res.push_back(matrix[x][y]);matrix[x][y] = INT_MIN; // 遍历过的数修改为 INT_MINint nx = x + dx[d], ny = y + dy[d];if (nx < 0 || nx >= n || ny < 0 || ny >= m || matrix[nx][ny] == INT_MIN) d = (d + 1) % 4;x += dx[d], y += dy[d];}return res;}
};
矩阵 - LeetCode 48. 旋转图像(中等)
【题目描述】
给定一个 n × n 的二维矩阵 matrix 表示一个图像。请你将图像顺时针旋转 90 度。
你必须在原地旋转图像,这意味着你需要直接修改输入的二维矩阵。请不要使用另一个矩阵来旋转图像。
【示例 1】
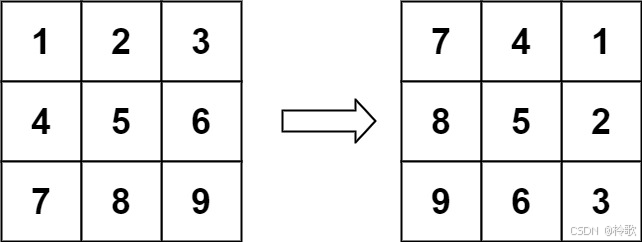
输入:matrix = [[1,2,3],[4,5,6],[7,8,9]]
输出:[[7,4,1],[8,5,2],[9,6,3]]
【示例 2】
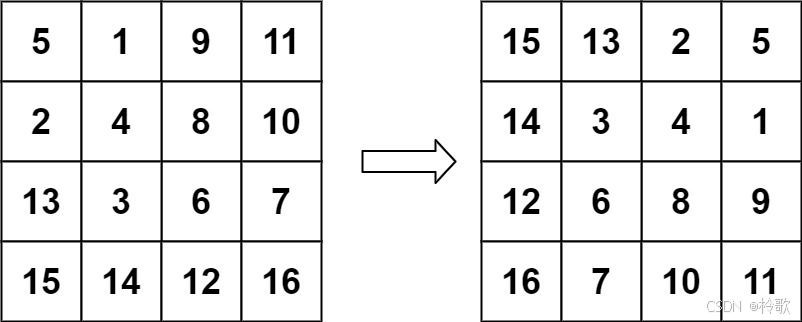
输入:matrix = [[5,1,9,11],[2,4,8,10],[13,3,6,7],[15,14,12,16]]
输出:[[15,13,2,5],[14,3,4,1],[12,6,8,9],[16,7,10,11]]
【提示】
n==matrix.length==matrix[i].lengthn == matrix.length == matrix[i].lengthn==matrix.length==matrix[i].length
1≤n≤201\le n\le 201≤n≤20
−1000≤matrix[i][j]≤1000-1000\le matrix[i][j]\le 1000−1000≤matrix[i][j]≤1000
【分析】
我们先给出一个变换过程的例子:
1 2 3 1 4 7 7 4 1
4 5 6 => 2 5 8 => 8 5 2
7 8 9 3 6 9 9 6 3
该过程很简单,但是没有接触过类似题目的话确实很难想出来,首先沿着主对角线进行翻转,然后沿着列的中轴进行翻转即可。
【代码】
class Solution {
public:void rotate(vector<vector<int>>& matrix) {int n = matrix.size();// 沿对角线翻转for (int i = 0; i < n; i++)for (int j = i + 1; j < n; j++)swap(matrix[i][j], matrix[j][i]);// 沿列中轴线翻转for (int i = 0; i < n; i++)for (int j = 0; j < n >> 1; j++)swap(matrix[i][j], matrix[i][n - 1 - j]);}
};
