【算法】分治

1. 快速排序

912. 排序数组 - 力扣（LeetCode）

        

         

    private void quickSort(int[] nums, int head, int tail) {// 递归出口if (head >= tail) {return;}// 数组分块的逻辑int key = nums[new Random().nextInt(tail - head + 1) + head];int left = head - 1, right = tail + 1, scan = head;while (scan < right) {if (nums[scan] < key) {left++;swap(nums, scan, left);scan++;} else if (nums[scan] > key) {right--;swap(nums, scan, right);} else {scan++;}}// 递归调用quickSort(nums, head, left);quickSort(nums, right, tail);}

75. 颜色分类 - 力扣（LeetCode）

        

        int len = nums.length, scan = 0, left = -1, right = len;while (scan < right) {if (nums[scan] == 0) {left++; swap(nums, scan, left);scan++;          } else if (nums[scan] == 2) {right--;swap(nums, scan, right);} else {scan++;}}

2. 快速选择

面试题 17.14. 最小K个数 - 力扣（LeetCode）

                

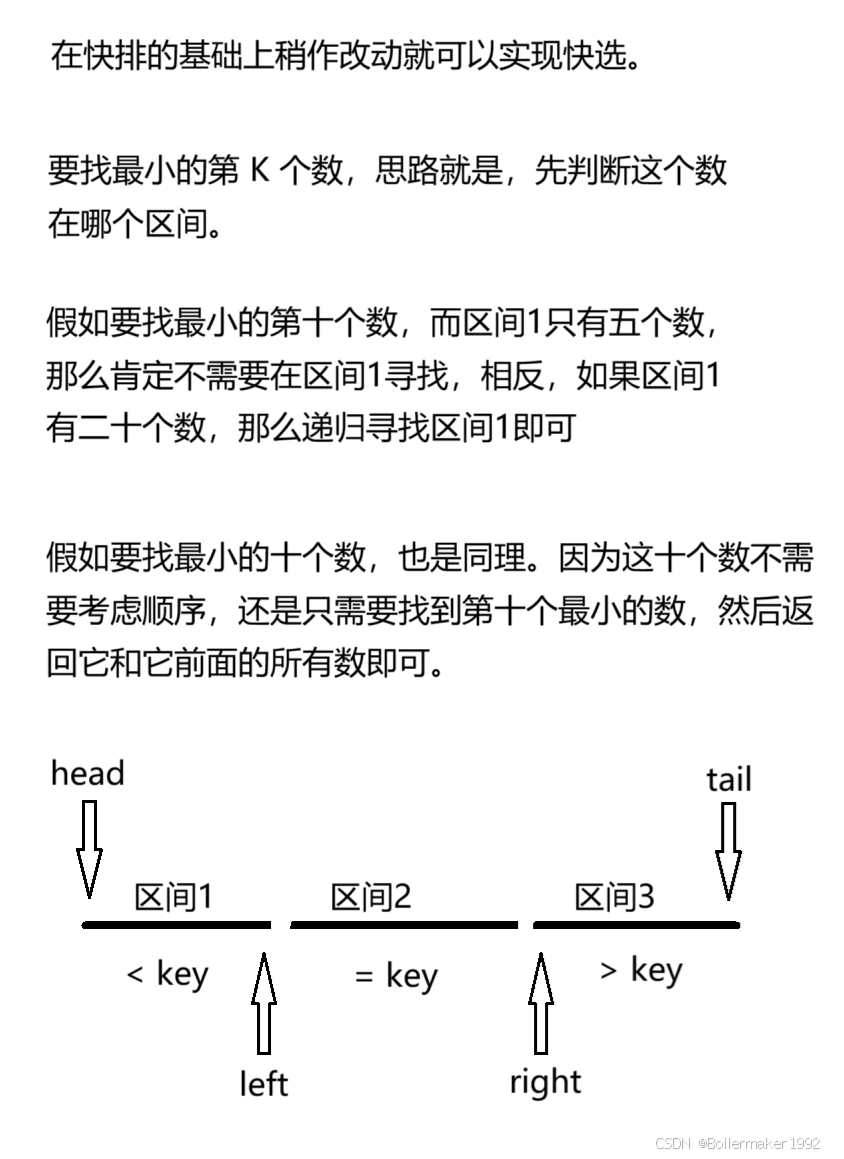
        // 在快排的基础上，改变递归条件即可if (left - head + 1 >= k) {quickSort(nums, k, head, left);} else if (right - head + 1 <= k) {quickSort(nums, k - (right - head), right, tail);} else {return;}

3. 归并排序

912. 排序数组 - 力扣（LeetCode）

        归并排序的思想类似快速排序，快速排序是先将数组大致排序，再递归，类似二叉树的前序遍历，归并排序是先递归，递归到最后再排序，层层返回排好序的结果，类似二叉树的后序遍历。

        

    private void mergeSort(int[] nums, int left, int right) {// 出口if (left >= right) {return;}// 递归调用int mid = (right + left) / 2;mergeSort(nums, left, mid);mergeSort(nums, mid + 1, right);// 为两个有序数组排序int s1 = left, e1 = mid, s2 = mid + 1, e2 = right;int i = 0;while (s1 <= e1 && s2 <= e2) {tempArr[i++] = nums[s1] < nums[s2] ? nums[s1++] : nums[s2++]; }while (s1 <= e1) {tempArr[i++] = nums[s1++];}while (s2 <= e2) {tempArr[i++] = nums[s2++];}        // 将合并后的结果写回原数组for (int j = left; j <= right; j++) {nums[j] = tempArr[j - left];}        }

LCR 170. 交易逆序对的总数 - 力扣（LeetCode）

        

                

                

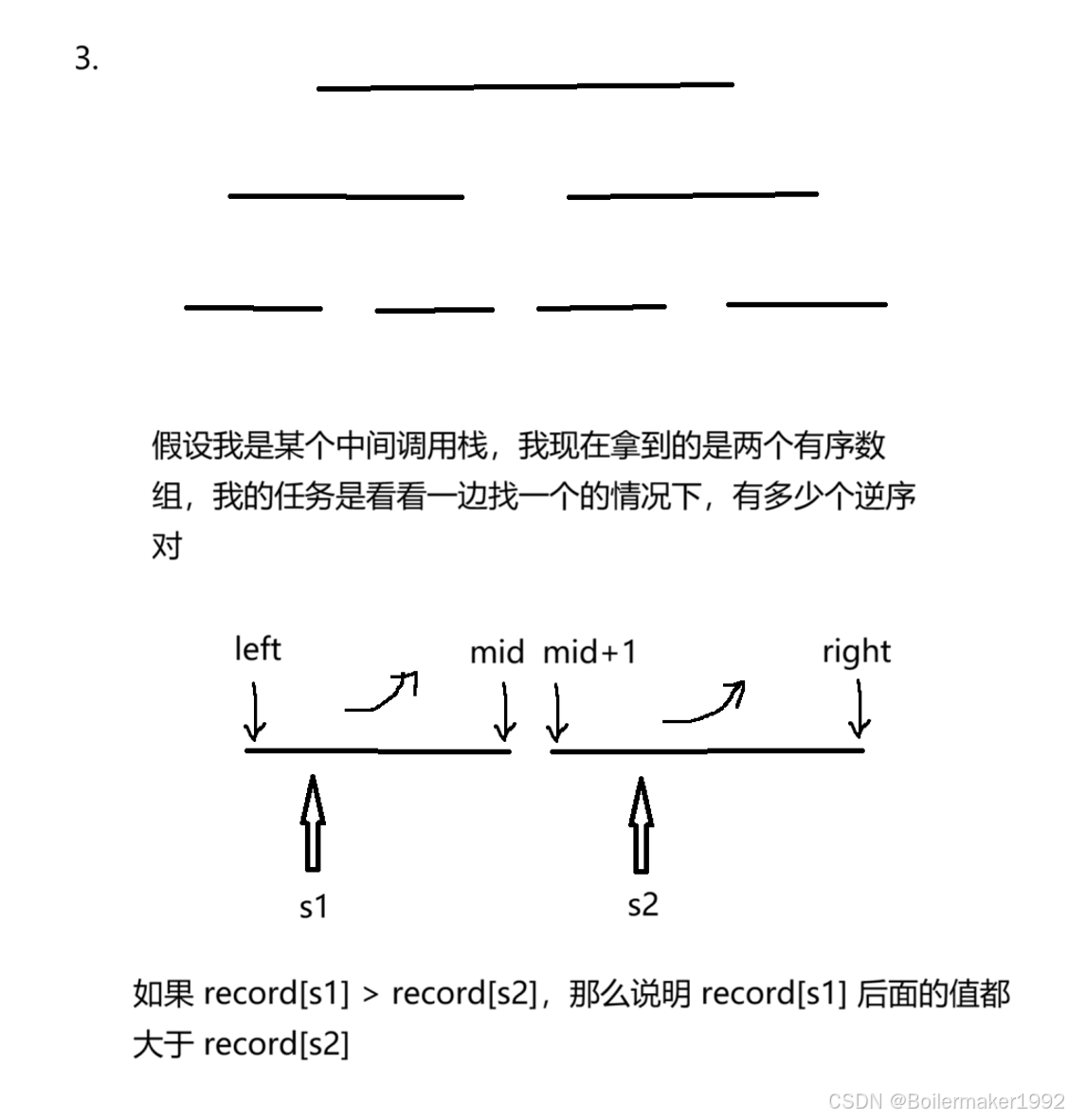
    private void mergeSort(int[] record, int left, int right) {if (left >= right) {return;}int mid = (left + right) / 2;mergeSort(record, left, mid);mergeSort(record, mid + 1, right);int s1 = left, e1 = mid, s2 = mid + 1, e2 = right;int i = 0;while (s1 <= e1 && s2 <= e2) {if (record[s1] <= record[s2]) {tempArr[i++] = record[s1++];} else {count += e1 - s1 + 1;tempArr[i++] = record[s2++];}}while (s1 <= e1) {tempArr[i++] = record[s1++];}while (s2 <= e2) {tempArr[i++] = record[s2++];}for (int j = left; j <= right; j++) {record[j] = tempArr[j - left];}      }

 315. 计算右侧小于当前元素的个数 - 力扣（LeetCode）

        这道题和上一道题类似，但是更麻烦一些。这道题相当于要我们分别记录每一个数所能形成的逆序对的数量，这需要角标能够对应得上。

        

        但是归并排序时，每层调用栈拿到的数组都是改变过位置的，这就需要我们手动记录角标的变化。只要我们始终明确，要统计的那个数最初所在的下标，就可以做到对号入座，分别记录了。

        

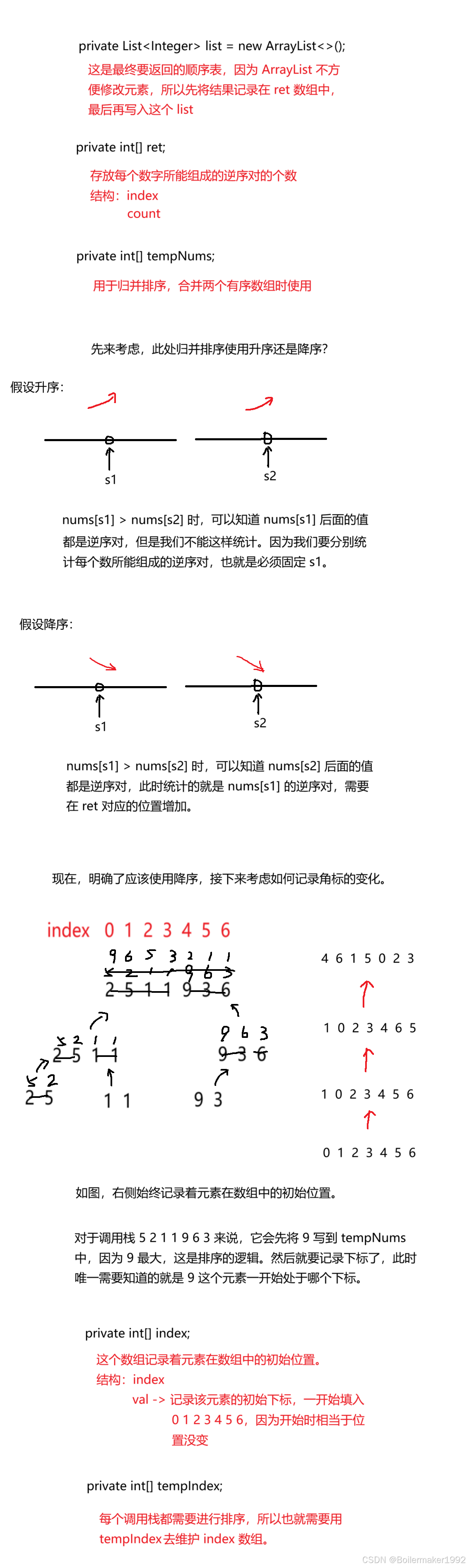
    private void mergeSort(int[] nums, int left, int right) {if (left >= right) {return;}int mid = (left + right) / 2;mergeSort(nums, left, mid);mergeSort(nums, mid + 1, right);int s1 = left, e1 = mid, s2 = mid + 1, e2 = right;int i = 0;while (s1 <= e1 && s2 <= e2) {if (nums[s1] <= nums[s2]) {tempIndex[i] = index[s2];tempNums[i++] = nums[s2++];} else {ret[index[s1]] += e2 - s2 + 1;tempIndex[i] = index[s1];tempNums[i++] = nums[s1++];}}while (s1 <= e1) {tempIndex[i] = index[s1];tempNums[i++] = nums[s1++];}while (s2 <= e2) {tempIndex[i] = index[s2];tempNums[i++] = nums[s2++];}for (int j = left; j <= right; j++) {index[j] = tempIndex[j - left];nums[j] = tempNums[j - left];}}

493. 翻转对 - 力扣（LeetCode）

        这道题类似于交易的逆序对那道题，唯一的区别就是，这道题的命中条件是 nums[i] > 2 * nums[j]，不再是 nums[i] > nums[j] 了。所以不能和归并排序的逻辑写到一起去，必须分开写。