当前位置：首页 > news >正文

LLM：Day1

news 2025/7/28 1:01:33

一、代码随想录

1、二分查找

二分查找涉及的很多的边界条件，逻辑比较简单，但就是写不好。例如到底是 while(left < right) 还是 while(left <= right)，到底是right = middle呢，还是要right = middle - 1呢？

写二分法，区间的定义一般为两种，左闭右闭即[left, right]，或者左闭右开即[left, right)。

a、左闭右闭:

while (left <= right) 要使用 <= ，因为left == right是有意义的，所以使用 <=
if (nums[middle] > target) right 要赋值为 middle - 1，因为当前这个nums[middle]一定不是target，那么接下来要查找的左区间结束下标位置就是 middle - 1

class Solution:def search(self, nums: List[int], target: int) -> int:left, right = 0, len(nums) - 1  # 定义target在左闭右闭的区间里，[left, right]while left <= right:middle = left + (right - left) // 2if nums[middle] > target:right = middle - 1  # target在左区间，所以[left, middle - 1]elif nums[middle] < target:left = middle + 1  # target在右区间，所以[middle + 1, right]else:return middle  # 数组中找到目标值，直接返回下标return -1  # 未找到目标值

b、左闭右开:

while (left < right)，这里使用 < ,因为left == right在区间[left, right)是没有意义的
if (nums[middle] > target) right 更新为 middle，因为当前nums[middle]不等于target，去左区间继续寻找，而寻找区间是左闭右开区间，所以right更新为middle，即：下一个查询区间不会去比较nums[middle]

class Solution:def search(self, nums: List[int], target: int) -> int:left, right = 0, len(nums)  # 定义target在左闭右开的区间里，即：[left, right)while left < right:  # 因为left == right的时候，在[left, right)是无效的空间，所以使用 <middle = left + (right - left) // 2if nums[middle] > target:right = middle  # target 在左区间，在[left, middle)中elif nums[middle] < target:left = middle + 1  # target 在右区间，在[middle + 1, right)中else:return middle  # 数组中找到目标值，直接返回下标return -1  # 未找到目标值

2、移除元素

双指针法

双指针法（快慢指针法）： 通过一个快指针和慢指针在一个for循环下完成两个for循环的工作。

定义快慢指针

快指针：寻找新数组的元素，新数组就是不含有目标元素的数组
慢指针：指向更新新数组下标的位置

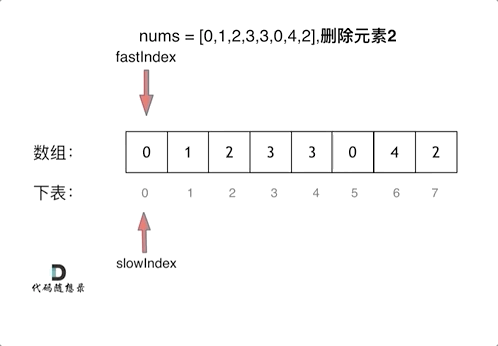
（版本一）快慢指针法
class Solution:def removeElement(self, nums: List[int], val: int) -> int:# 快慢指针fast = 0  # 快指针slow = 0  # 慢指针size = len(nums)while fast < size:  # 不加等于是因为，a = size 时，nums[a] 会越界# slow 用来收集不等于 val 的值，如果 fast 对应值不等于 val，则把它与 slow 替换if nums[fast] != val:nums[slow] = nums[fast]slow += 1fast += 1return slow

3、有序数组的平方

双指针法

数组其实是有序的，只不过负数平方之后可能成为最大数了。

那么数组平方的最大值就在数组的两端，不是最左边就是最右边，不可能是中间。

此时可以考虑双指针法了，i指向起始位置，j指向终止位置。

定义一个新数组result，和A数组一样的大小，让k指向result数组终止位置。

如果A[i] * A[i] < A[j] * A[j] 那么result[k--] = A[j] * A[j]; 。

如果A[i] * A[i] >= A[j] * A[j] 那么result[k--] = A[i] * A[i]; 。

（版本一）双指针法
class Solution:def sortedSquares(self, nums: List[int]) -> List[int]:l, r, i = 0, len(nums)-1, len(nums)-1res = [float('inf')] * len(nums) # 需要提前定义列表，存放结果while l <= r:if nums[l] ** 2 < nums[r] ** 2: # 左右边界进行对比，找出最大值res[i] = nums[r] ** 2r -= 1 # 右指针往左移动else:res[i] = nums[l] ** 2l += 1 # 左指针往右移动i -= 1 # 存放结果的指针需要往前平移一位return res

（版本二）暴力排序法
class Solution:def sortedSquares(self, nums: List[int]) -> List[int]:for i in range(len(nums)):nums[i] *= nums[i]nums.sort()return nums

二、LeetCode

1、两数之和的哈希表解法

数据结构选择：
- 使用字典（dict）作为哈希表，利用其 O (1) 的平均查找复杂度
- 字典的键是数组元素值，值是该元素对应的索引位置
遍历方式：
- 使用enumerate(nums)同时获取元素的索引i和值num
- 只需要一次遍历数组，时间复杂度为 O (n)
互补数计算：
- 对于当前元素num，计算complement = target - num
- 这是核心思路：两数之和为目标值 → 另一个数 = 目标值 - 当前数
查找与存储时机：
- 先检查互补数是否已在哈希表中（哈希表中存的是之前遍历过的元素）
- 若存在则直接返回结果，若不存在则将当前元素存入哈希表
- 这种 "先查后存" 的顺序避免了同一元素被重复使用

示例执行过程

以 nums = [3, 2, 4], target = 6 为例：

第一次循环（i=0, num=3）：
- complement = 6 - 3 = 3
- 哈希表为空，3 不在其中
- 存入 {3:0}，哈希表现在是 {3:0}
第二次循环（i=1, num=2）：
- complement = 6 - 2 = 4
- 4 不在哈希表中（当前哈希表只有 3）
- 存入 {2:1}，哈希表现在是 {3:0, 2:1}
第三次循环（i=2, num=4）：
- complement = 6 - 4 = 2
- 检查发现 2 在哈希表中，其索引是 1
- 立即返回 [1, 2]（这两个索引对应的元素 2+4=6）

class Solution(object):def twoSum(self, nums, target):hashtable = dict()  # 初始化一个空字典作为哈希表# 遍历数组，enumerate同时获取索引i和元素值numfor i, num in enumerate(nums):# 计算需要寻找的互补数：目标值 - 当前元素值complement = target - num# 检查互补数是否已经在哈希表中if complement in hashtable:# 如果存在，返回互补数的索引和当前元素的索引return [hashtable[complement], i]# 如果不存在，将当前元素和其索引存入哈希表hashtable[num] = i# 如果遍历完所有元素都没有找到，返回空列表return []

2、统计小于目标和的对数

相向双指针

思路
题目相当于从数组中选两个数，我们只关心这两个数的和是否小于 target，由于 a+b=b+a，无论如何排列数组元素，都不会影响加法的结果，所以排序不影响答案。比如 nums=[1,2], target=4 和 nums=[2,1], target=4 算出来的答案都是 1，可见排序并不影响结果。

排序后：

初始化左右指针 left=0, right=n−1。
如果 nums[left]+nums[right]<target，由于数组是有序的，nums[left] 与下标 i 在区间 [left+1,right] 中的任何 nums[i] 相加，都是 <target 的，因此直接找到了 right−left 个合法数对，加到答案中，然后将 left 加一。
如果 nums[left]+nums[right]≥target，由于数组是有序的，nums[right] 与下标 i 在区间 [left,right−1] 中的任何 nums[i] 相加，都是 ≥target 的，因此后面无需考虑 nums[right]，将 right 减一。
重复上述过程直到 left≥right 为止。

class Solution(object):def countPairs(self, nums, target):nums.sort()flag = 0left = 0right = len(nums) -1while (left < right):sum = nums[left] + nums[right]if sum < target:flag = flag + right -leftleft = left + 1else:right = right-1return flag

3、最接近的三数之和

排序后，枚举 nums[i] 作为第一个数，那么问题变成找到另外两个数，使得这三个数的和与 target 最接近，这同样可以用双指针解决。

设 s=nums[i]+nums[j]+nums[k]，为了判断 s 是不是与 target 最近的数，我们还需要用一个变量 minDiff 维护 ∣s−target∣ 的最小值。分类讨论：

如果 s=target，那么答案就是 s，直接返回 s。
如果 s>target，那么如果 s−target<minDiff，说明找到了一个与 target 更近的数，更新 minDiff 为 s−target，更新答案为 s。然后和三数之和一样，把 k 减一。
否则 s<target，那么如果 target−s<minDiff，说明找到了一个与 target 更近的数，更新 minDiff 为 target−s，更新答案为 s。然后和三数之和一样，把 j 加一。

除此以外，还有以下几个优化：

设 s=nums[i]+nums[i+1]+nums[i+2]。如果 s>target，由于数组已经排序，后面无论怎么选，选出的三个数的和不会比 s 还小，所以不会找到比 s 更优的答案了。所以只要 s>target，就可以直接 break 外层循环了。在 break 前判断 s 是否离 target 更近，如果更近，那么更新答案为 s。

设 s=nums[i]+nums[n−2]+nums[n−1]。如果 s<target，由于数组已经排序，nums[i] 加上后面任意两个数都不超过 s，所以下面的双指针就不需要跑了，无法找到比 s 更优的答案。但是后面还有更大的 nums[i]，可能找到一个离 target 更近的三数之和，所以还需要继续枚举，continue 外层循环。在 continue 前判断 s 是否离 target 更近，如果更近，那么更新答案为 s，更新 minDiff 为 target−s。

如果 i>0 且 nums[i]=nums[i−1]，那么 nums[i] 和后面数字相加的结果，必然在之前算出过，所以无需跑下面的双指针，直接 continue 外层循环。（可以放在循环开头判断。）

class Solution:def threeSumClosest(self, nums: List[int], target: int) -> int:nums.sort()n = len(nums)min_diff = inffor i in range(n - 2):x = nums[i]if i and x == nums[i - 1]:continue  # 优化三# 优化一s = x + nums[i + 1] + nums[i + 2]if s > target:  # 后面无论怎么选，选出的三个数的和不会比 s 还小if s - target < min_diff:ans = s  # 由于下一行直接 break，这里无需更新 min_diffbreak# 优化二s = x + nums[-2] + nums[-1]if s < target:  # x 加上后面任意两个数都不超过 s，所以下面的双指针就不需要跑了if target - s < min_diff:min_diff = target - sans = scontinue# 双指针j, k = i + 1, n - 1while j < k:s = x + nums[j] + nums[k]if s == target:return sif s > target:if s - target < min_diff:  # s 与 target 更近min_diff = s - targetans = sk -= 1else:  # s < targetif target - s < min_diff:  # s 与 target 更近min_diff = target - sans = sj += 1return ans

4、四数之和

思路和 15. 三数之和一样，排序后，枚举 nums[a] 作为第一个数，枚举 nums[b] 作为第二个数，那么问题变成找到另外两个数，使得这四个数的和等于 target，这可以用双指针解决。

优化思路也和视频中讲的一样，对于 nums[a] 的枚举：

设 s=nums[a]+nums[a+1]+nums[a+2]+nums[a+3]。如果 s>target，由于数组已经排序，后面无论怎么选，选出的四个数的和不会比 s 还小，所以后面不会找到等于 target 的四数之和了。所以只要 s>target，就可以直接 break 外层循环了。

设 s=nums[a]+nums[n−3]+nums[n−2]+nums[n−1]。如果 s<target，由于数组已经排序，nums[a] 加上后面任意三个数都不会超过 s，所以无法在后面找到另外三个数与 nums[a] 相加等于 target。但是后面还有更大的 nums[a]，可能出现四数之和等于 target 的情况，所以还需要继续枚举，continue 外层循环。

如果 a>0 且 nums[a]=nums[a−1]，那么 nums[a] 和后面数字相加的结果，必然在之前算出过，所以无需执行后续代码，直接 continue 外层循环。（可以放在循环开头判断。）

对于 nums[b] 的枚举（b 从 a+1 开始），也同样有类似优化：

设 s=nums[a]+nums[b]+nums[b+1]+nums[b+2]。如果 s>target，由于数组已经排序，后面无论怎么选，选出的四个数的和不会比 s 还小，所以后面不会找到等于 target 的四数之和了。所以只要 s>target，就可以直接 break。

设 s=nums[a]+nums[b]+nums[n−2]+nums[n−1]。如果 s<target，由于数组已经排序，nums[a]+nums[b] 加上后面任意两个数都不会超过 s，所以无法在后面找到另外两个数与 nums[a] 和 nums[b] 相加等于 target。但是后面还有更大的 nums[b]，可能出现四数之和等于 target 的情况，所以还需要继续枚举，continue。

如果 b>a+1 且 nums[b]=nums[b−1]，那么 nums[b] 和后面数字相加的结果，必然在之前算出过，所以无需执行后续代码，直接 continue。注意这里 b>a+1 的判断是必须的，如果不判断，对于示例 2 这样的数据，会直接 continue，漏掉符合要求的答案。

class Solution(object):def fourSum(self, nums, target):nums.sort()ans = []n = len(nums)for a in range(n-3):if a>0 and nums[a] == nums[a-1]:continueif nums[a]+ nums[a+1] +nums[a+2] +nums[a+3] > target:breakif nums[a]+nums[-1]+nums[-2]+nums[-3] < target:continuefor b in range(a+1, n-2):if b>a+1 and nums[b] == nums[b-1]:continueif nums[a]+nums[b]+nums[b+1]+nums[b+2] > target:breakif nums[a]+nums[b]+nums[-1]+nums[-2] < target:continuec = b+1d = n-1while c < d:if nums[a]+nums[b]+nums[c]+nums[d] <target:c += 1elif nums[a]+nums[b]+nums[c]+nums[d] >target:       d -= 1else:ans.append([nums[a], nums[b], nums[c], nums[d]])while c < d and nums[c] == nums[c - 1]:  # 跳过重复数字c += 1d -= 1while d > c and nums[d] == nums[d + 1]:  # 跳过重复数字d -= 1return ans