一文读懂深度模型优化器，掌握炼丹工具

深度模型优化器是训练神经网络的核心工具，其目标是高效地找到损失函数的最小值。从基础的随机梯度下降（SGD）到结合一阶动量修正与两阶段更新的Ranger，优化器的发展始终围绕着加速收敛、提升稳定性、适应参数差异和增强泛化能力四大核心目标。以下从简单到复杂逐步梳理优化器的演进脉络，分析其公式、思想、优劣及改进方向，并总结实用训练技巧。

优化器的主要改进目标有以下几个方向：

• 更快的收敛速度
• 更稳定的收敛效果
• 更泛化的拟合能力
  

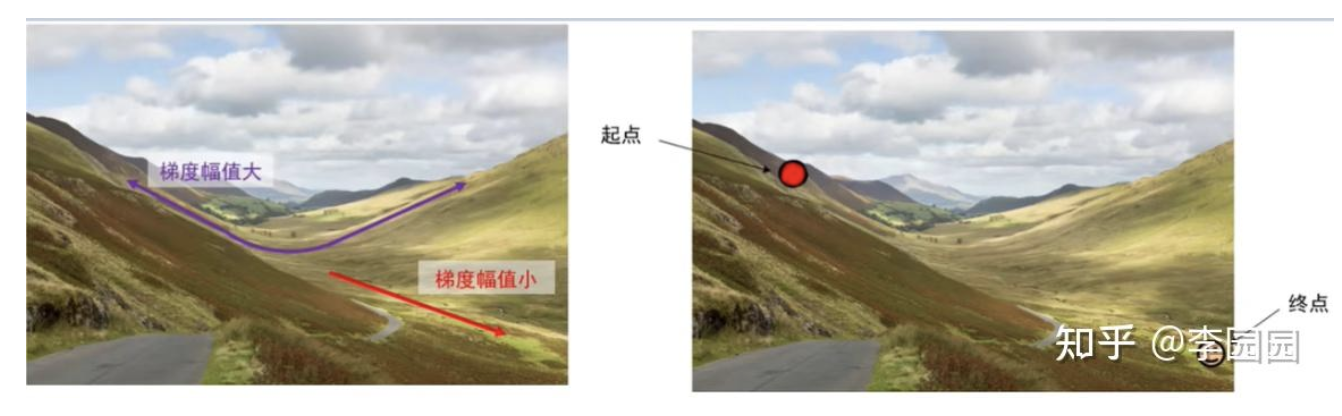
一、基础优化器：随机梯度下降（SGD）

SGD是最基础的优化器，也是后续所有优化器的起点。其核心思想是利用随机采样的批次数据计算梯度，并基于梯度方向更新参数。

1. 公式
   参数更新公式：
   $${\theta }_{t+1}={\theta }_t-\eta \cdot \nabla L({\theta }_t;{\mathcal{B}}_t)$$
   其中：
   • ${\theta }_t$ 是t时刻的参数；
   • $\eta$ 是学习率（全局固定）；
   • $\nabla L({\theta }_t;{\mathcal{B}}_t)$ 是基于批次数据${\mathcal{B}}_t$计算的损失函数梯度；
   • $\eta \cdot \nabla L$ 是参数更新量。
2. 核心思想
   基于 “梯度下降” 原理：损失函数沿梯度方向下降最快，因此每次更新参数时，朝着梯度的反方向移动，移动步长由学习率$\eta$控制。“随机” 体现在用批次数据（而非全量数据）计算梯度，降低计算成本。
3. 优劣分析

• 优点：
  • 实现简单，内存占用极低（仅需存储当前梯度）；
  • 适合大规模数据或高维模型（如深度学习）；
  • 随机性可能帮助跳出局部最优，泛化能力较强（相比全量梯度下降）。
• 缺点：
  • 收敛速度慢：梯度方向受批次噪声影响大，更新路径震荡剧烈（尤其在高维非凸函数中）；
  • 对学习率敏感：$\eta$过大易发散，过小则收敛过慢；
  • 难以应对 “沟壑区域”：在梯度方向频繁变化的区域（如损失函数的 “沟壑”），更新方向反复震荡，效率极低。

4. 改进方向
   SGD 的核心问题是缺乏对历史梯度的利用，导致更新方向不稳定。因此，第一个改进方向是引入 “动量” 以平滑梯度震荡，模拟物理中的 “惯性” 效应。
   

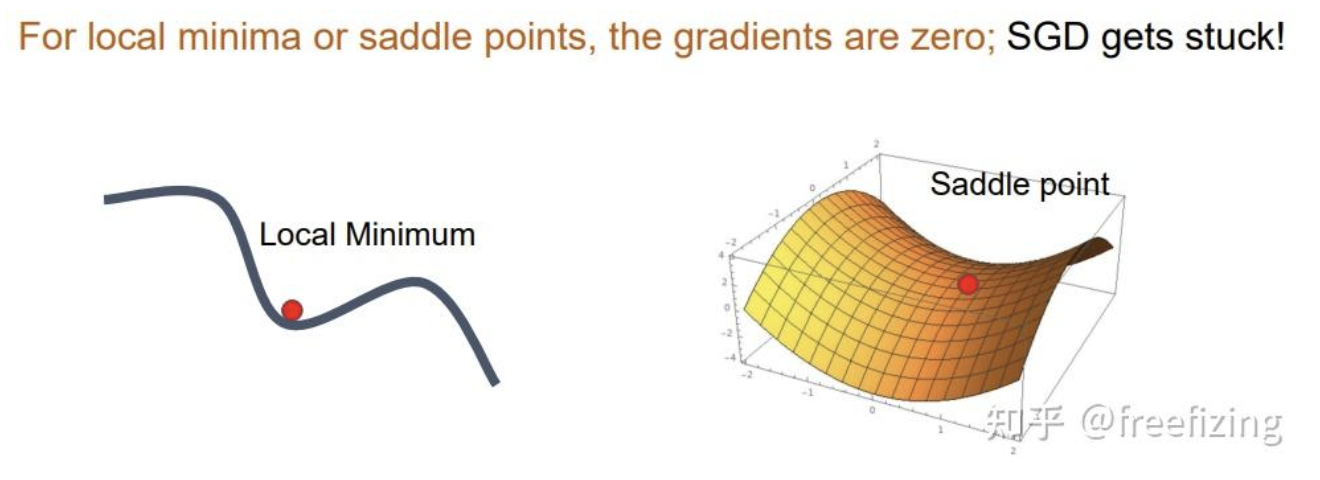
二、一阶动量优化器：SGD with Momentum 与 Nesterov Momentum

为解决 SGD 的震荡问题，动量（Momentum）优化器通过累积历史梯度方向，减少随机噪声的影响，加速收敛。

1. SGD with Momentum（动量 SGD）
   公式
   引入“动量项”$m_t$（累积历史梯度的加权和），参数更新公式：
   $$\begin{array}{rl}{m}_t& =\gamma \cdot m_{t-1}+\nabla L({\theta }_t;{\mathcal{B}}_t)\\ {\theta }_{t+1}& ={\theta }_t-\eta \cdot m_t\end{array}$$
   其中：

   • $\gamma$ 是动量衰减系数（通常取 0.9），控制历史梯度的权重；
   • $m_t$ 可理解为 “累积梯度”，融合了当前梯度与历史动量（类似物理中的 “惯性”）。

   
   核心思想

   • 模拟物体运动的 “惯性”：若连续多步梯度方向一致（如沿 “沟壑” 的下坡方向），动量项会累积能量，加速收敛；若梯度方向突变（如噪声导致），动量项会平滑震荡（历史方向抑制突变）。

   优劣分析

   • 优点：相比纯 SGD，收敛速度提升 2-3 倍，震荡显著减少，尤其在 “沟壑区域” 表现更稳定。
   • 缺点：动量可能导致 “过冲”（动量过大时，参数超过最优值后难以回调）；对梯度方向的 “预判” 不足，在梯度方向即将变化时仍会延续历史方向。

2. Nesterov Momentum（涅斯捷罗夫动量）
   为解决动量 SGD 的 “过冲” 问题，Nesterov 动量引入 “提前更新” 机制，先基于当前动量预判下一步位置，再计算梯度，提升方向准确性。
   
   公式
   参数更新分两步：

   • 先基于当前动量 “预判” 一步更新：${\tilde{\theta }}_t={\theta }_t-\gamma \cdot m_{t-1}$；
   • 基于预判位置计算梯度，再更新动量和参数：
     $$\begin{array}{rl}{m}_t& =\gamma \cdot m_{t-1}+\nabla L({\tilde{\theta }}_t;{\mathcal{B}}_t)\\ {\theta }_{t+1}& ={\theta }_t-\eta \cdot m_t\end{array}$$

   核心思想
   “先移动，再看方向”：通过预判位置${\tilde{\theta }}_t$计算梯度，相当于提前修正动量方向，减少因历史动量导致的偏差。例如，若参数即将进入 “上坡” 区域，预判后计算的梯度会更早抑制动量，避免过冲。
   
   优劣分析

   • 优点：比普通动量收敛更精准，过冲现象减少，在凸优化问题中理论收敛速度更快。
   • 缺点：实现略复杂，在非凸问题（如深度学习）中优势不如凸问题明显。

3. 改进方向
   动量优化器解决了 “震荡与收敛速度” 问题，但仍存在一个核心缺陷：学习率全局固定。神经网络中不同参数的梯度特性差异很大（如稀疏特征的参数梯度小，密集特征的梯度大），固定学习率无法适配这种差异。因此，下一步改进是引入 “自适应学习率”。

三、一阶动量 + 自适应学习率：AdaGrad、RMSprop 与 Adam

自适应学习率优化器的核心是：为每个参数分配独立的学习率，梯度大的参数学习率小（避免更新过度），梯度小的参数学习率大（加速收敛）。

1. AdaGrad（自适应梯度）
   AdaGrad 是首个实现参数自适应学习率的优化器，通过累积参数的历史梯度平方来动态调整学习率。
   公式
   参数更新公式：
   $$\begin{array}{rl}{g}_t& =\nabla L({\theta }_t;{\mathcal{B}}_t)\\ h_t& =h_{t-1}+g_t^2(\text{累积梯度平方，初始}{h}_0=0)\\ {\theta }_{t+1}& ={\theta }_t-\frac{\eta }{\sqrt{h_t+ϵ}}\cdot g_t\end{array}$$
   其中：

   • $h_t$ 是参数的 “梯度平方累积和”（每个参数独立累积）；
   • $ϵ\approx 10^{-8}$ 是防止分母为 0 的微小常数；
   • $\frac{\eta }{\sqrt{h_t+ϵ}}$ 是参数的自适应学习率（梯度平方越大，学习率越小）。

   核心思想
   “梯度大的参数慢更，梯度小的参数快更”：例如，文本中的稀疏特征（如低频词）梯度小，$h_t$累积慢，学习率较大，可快速更新；高频特征梯度大，$h_t$累积快，学习率较小，避免震荡。

   优劣分析

   • 优点：适合稀疏数据（如 NLP、推荐系统），能自适应参数差异。
   • 缺点：$h_t$随训练步数单调递增，导致学习率逐渐趋近于 0，最终参数更新停滞（训练提前终止）。

2. RMSprop（均方根传播）
   为解决 AdaGrad 学习率 “单调衰减至 0” 的问题，RMSprop 用指数移动平均（EMA） 替代梯度平方的累积和，使$h_t$更关注近期梯度，避免学习率过早消失。
   公式
   参数更新公式：
   $$\begin{array}{rl}{g}_t& =\nabla L({\theta }_t;{\mathcal{B}}_t)\\ h_t& =\gamma \cdot h_{t-1}+(1-\gamma )\cdot g_t^2(\gamma \approx 0.9)\\ {\theta }_{t+1}& ={\theta }_t-\frac{\eta }{\sqrt{h_t+ϵ}}\cdot g_t\end{array}$$
   核心思想
   用 EMA 平滑$h_t$：$h_t$是 “近期梯度平方的加权平均”（$\gamma$控制历史权重衰减），而非全量累积。例如，$\gamma =0.9$时，$h_t$主要由最近 10 步的梯度平方决定，避免长期累积导致的学习率消失。
   优劣分析

   • 优点：解决了 AdaGrad 的学习率衰减问题，收敛更稳定，适合在线学习（流式数据）。
   • 缺点：仅关注梯度的 “大小”（二阶矩），未考虑梯度的 “方向”（一阶矩），在梯度方向变化剧烈的场景中收敛速度仍有限。

3. Adam（自适应动量， Adaptive Moment Estimation）
   Adam 是优化器发展的里程碑，它融合了动量（一阶矩）和 RMSprop（二阶矩）的优点，同时考虑梯度的方向和大小，实现 “方向稳健 + 步长自适应”。
   公式
   参数更新分三步：

   • 计算一阶矩（动量项，关注方向）：
     $$m_t={\beta }_1\cdot m_{t-1}+(1-{\beta }_1)\cdot g_t({\beta }_1\approx 0.9)$$
   • 计算二阶矩（梯度平方的 EMA，关注大小）：
     $$v_t={\beta }_2\cdot v_{t-1}+(1-{\beta }_2)\cdot g_t^2({\beta }_2\approx 0.999)$$
   • 修正一阶矩和二阶矩的偏差（训练初期$m_t$和$v_t$偏小）：
     $${\hat{m}}_t=\frac{m_t}{1-{\beta }_1^t},{\hat{v}}_t=\frac{v_t}{1-{\beta }_2^t}$$
   • 参数更新：
     $${\theta }_{t+1}={\theta }_t-\frac{\eta }{\sqrt{{\hat{v}}_t}+ϵ}\cdot {\hat{m}}_t$$

   核心思想

   • 一阶矩$m_t$：累积梯度方向（类似动量），减少方向震荡；
   • 二阶矩$v_t$：累积梯度大小（类似 RMSprop），自适应步长；
   • 偏差修正：训练初期（t较小时），${\beta }_1^t$和${\beta }_2^t$较大，修正后${\hat{m}}_t$和${\hat{v}}_t$更接近真实值，避免低估。

   优劣分析

   • 优点：收敛速度快（比 SGD 快 5-10 倍），稳定性强（兼顾方向和大小），适用场景广（CV、NLP、推荐等）。
   • 缺点：
     • 泛化能力可能弱于 SGD：自适应学习率可能导致过拟合（尤其在小数据集上）；
     • 小批量偏差：当批次大小过小时（如$batch=1$），${\hat{m}}_t$和${\hat{v}}_t$估计误差大，更新不稳定。

4. AdamW
   AdamW（Adam with Weight Decay）的核心算法原理和 Adam 是一样的，也是基于梯度的一阶矩和二阶矩估计来更新参数。但它在权重衰减（weight decay）的实现方式上进行了改进，使其更符合 L2 正则化的本质含义。
   对正则化的处理方式

   • Adam 优化器：在 Adam 中，若要使用 L2 正则化（权重衰减），通常是在计算梯度时直接将正则化项加入到损失函数中，然后计算带有正则化项的梯度。即：
     $$g_t=\nabla \left(L({\theta }_t)+\lambda {\theta }_t\right)$$其中$\lambda$是正则化系数。这种方式下，正则化项会参与到一阶矩和二阶矩的计算中。
   • AdamW 优化器：AdamW 将权重衰减从损失函数中分离出来，不把它纳入到梯度计算中，而是直接在参数更新时应用权重衰减，公式为：$${\theta }_{t+1}=(1-\lambda \eta ){\theta }_t-\frac{\eta }{\sqrt{{\hat{v}}_t}+ϵ}\cdot {\hat{m}}_t$$这样，权重衰减就独立于自适应学习率机制，避免了自适应学习率对权重衰减的影响，使得权重衰减更加稳定和合理。

   实际表现

   • Adam 优化器：在一些场景下，由于正则化项参与了一阶矩和二阶矩的计算，可能会导致在训练后期，随着自适应学习率的变化，正则化的效果变得不稳定，从而容易出现过拟合的情况，尤其是在数据量较小或者模型较复杂时。
   • AdamW 优化器：因为其合理的权重衰减实现方式，使得在训练过程中能够更有效地抑制过拟合，在许多实验中，特别是在像自然语言处理、计算机视觉等领域的大规模模型训练任务中，AdamW 相比 Adam 能取得更好的泛化性能，在验证集和测试集上表现出更低的误差。

   应用场景

   • Adam 优化器：适用于一些对计算资源要求不是特别高，且对模型泛化性能要求不是极致严格的简单实验或者小型项目中，在快速验证想法和初步训练模型时可以使用。
   • AdamW 优化器：更适合于大规模、复杂的深度学习模型训练任务，尤其是在需要关注模型泛化能力，防止过拟合的场景，比如 BERT 等预训练语言模型的训练中被广泛应用。

5. 改进方向
   Adam/AdamW的核心问题是小批量场景下的一阶矩估计偏差。后续的 RAdam（Rectified Adam）通过动态判断矩估计的 “稳定性”，在不稳定阶段切换为动量 SGD 更新，解决了这一缺陷。

四、二阶优化器：牛顿法与拟牛顿法

一阶优化器（SGD、Adam 等）仅利用梯度（一阶导数），而二阶优化器引入 Hessian 矩阵（二阶导数），考虑损失函数的 “曲率”，理论上收敛速度更快。

1. 牛顿法
   牛顿法的核心是用二次函数近似损失函数，利用 Hessian 矩阵的逆（曲率信息）调整更新方向，实现 “精准步长”。
   公式
   参数更新公式：
   $${\theta }_{t+1}={\theta }_t-H^{-1}({\theta }_t)\cdot \nabla L({\theta }_t)$$
   其中：

   • $H({\theta }_t)$ 是损失函数在${\theta }_t$处的 Hessian 矩阵（二阶导数矩阵），描述函数的曲率；
   • $H^{-1}\cdot \nabla L$ 是结合曲率的更新量（步长由曲率决定）。

   
   核心思想
   一阶优化器的更新方向是 “梯度反方向”，而牛顿法的更新方向是 “梯度反方向除以曲率”：在曲率大的区域（梯度变化快），步长自动减小；在曲率小的区域（梯度变化慢），步长自动增大。对于二次函数，牛顿法可 “一步收敛”，远快于一阶方法。
   
   优劣分析

   • 优点：收敛速度快（二次收敛），步长自适应（无需手动调学习率）。
   • 缺点：
     • 计算成本极高：Hessian 矩阵是$n\times n$（n为参数数量，深度学习中n可达百万级），存储和求逆的复杂度为$O(n^3)$，完全无法适用于大规模模型；
     • 非正定风险：Hessian 矩阵可能非正定（特征值为负），导致更新方向错误（反而远离最小值）。

2. 拟牛顿法（BFGS 与 L-BFGS）
   为降低牛顿法的计算成本，拟牛顿法用近似矩阵替代 Hessian 逆，通过梯度的变化量迭代更新近似矩阵，避免直接计算二阶导数。
   
   核心思想
   （以 BFGS 为例）用矩阵$B_t$近似 Hessian 矩阵H，或用$D_t$近似$H^{-1}$；
   迭代更新规则：
   $$\begin{gathered} D_{t+1}=(I-{\rho }_t{s}_t{y}_t^T)D_t(I-{\rho }_t{y}_t{s}_t^T)+{\rho }_t{s}_t{s}_t^T \\ （其中s_t={\theta }_{t+1}-{\theta }_t，y_t=\nabla L_{t+1}-\nabla L_t) \end{gathered}$$
   最终更新公式：
   $${\theta }_{t+1}={\theta }_t-D_t\cdot \nabla L_t$$
   优劣分析

   • 优点：比牛顿法计算成本低（无需求 Hessian 逆），收敛速度快于一阶方法。
   • 缺点：
     • BFGS 仍需存储$n\times n$的近似矩阵（不适合高维模型）；
     • L-BFGS（Limited-memory BFGS）通过存储最近m步的梯度变化降低内存，但计算复杂度仍高于一阶方法（尤其在批量大时），因此在深度学习中应用有限。

3. 改进方向
   二阶方法的核心瓶颈是高维场景下的计算与存储成本。目前实用化的改进是 “轻量级二阶近似”（如 K-FAC，用 Fisher 信息矩阵近似 Hessian），但尚未普及。

五、RAdam

RAdam 通过动态调整自适应学习率的方差来解决 Adam 在小批量场景下的不稳定性，核心机制包括以下三点：

1. 动态判断是否启用自适应学习率
   RAdam 引入了一个自由度参数${\rho }_t$，其计算公式为：
   $${\rho }_t=\frac{2}{1-{\beta }_2}-2\cdot \frac{1-{\beta }_2^t}{1-{\beta }_2}+1$$
   其中，${\beta }_2$是 Adam 中二阶矩的衰减系数（通常取 0.999）。当${\rho }_t\le 4$时，RAdam 认为当前小批量的梯度估计方差过大（如 batch size 过小或训练初期数据不足），此时禁用自适应学习率，直接采用动量 SGD 的更新方式：
   $${\theta }_{t+1}={\theta }_t-\eta \cdot m_t$$
   这一策略避免了 Adam 在小批量时因二阶矩估计偏差导致的学习率剧烈波动
2. 整流项抑制方差放大
   当${\rho }_t>4$时，RAdam 恢复 Adam 的自适应学习率，但通过整流项$r(t)$对学习率进行修正：
   $$r(t)=\sqrt{\frac{({\rho }_t-4)({\rho }_t-2){\rho }_{\infty }}{({\rho }_{\infty }-4)({\rho }_{\infty }-2){\rho }_t}}$$
   其中，${\rho }_{\infty }=\frac{2}{1-{\beta }_2}-1$是理论最大自由度。整流项$r(t)$通过调整二阶矩的缩放因子，抑制小批量梯度噪声对方差估计的放大效应，使学习率更稳定。
3. 自动实现动态warmup
   Adam 在小批量时需要手动设置 warmup 阶段以降低初始方差，但 RAdam 通过上述动态机制自动完成 warmup。例如，在训练初期（t较小），${\rho }_t$可能小于 4，此时 RAdam 切换为动量 SGD，逐步累积稳定的梯度统计量后再启用自适应学习率，避免了 Adam 因初始方差过大导致的参数震荡

思考1: 为什么 Adam 在小批量时不稳定，而 SGD 更稳定?

1. Adam 的不稳定性根源：梯度估计的方差放大
   Adam 的自适应学习率依赖梯度的一阶矩和二阶矩估计，但小批量梯度的方差会随着 batch size 的减小而显著增加。例如，当 batch size=1 时，梯度估计的方差是全量梯度的$1/N$倍（N为总样本数），导致 Adam 的二阶矩$v_t$被噪声污染，学习率$\eta /\sqrt{v_t}$剧烈波动。
   此外，Adam 的偏差修正项$\frac{1}{1-{\beta }_2^t}$在训练初期（t小）会放大这种噪声，进一步加剧不稳定性。例如，当$t=10$且${\beta }_2=0.999$时，修正因子约为 1000，可能将微小的梯度波动放大为学习率的剧烈变化

2. SGD 的稳定性机制：噪声鲁棒性
   SGD 直接使用当前小批量的梯度更新参数，不依赖历史统计量，因此对梯度噪声具有天然的鲁棒性。例如，当 batch size=1 时，SGD 的更新方向完全由单个样本的梯度决定，虽然噪声大，但这种 “随机扰动” 反而帮助模型探索更广泛的参数空间，避免陷入局部最优。
   此外，SGD 的学习率是全局固定的，不会因个别参数的梯度波动而改变整体更新步长，从而在小批量场景下保持稳定。

思考2: 为什么 SGD 的泛化能力优于 Adam？

1. 噪声正则化效应SGD 的小批量梯度噪声相当于一种隐式正则化，迫使模型学习更鲁棒的特征表示。例如，在高维非凸损失函数中，噪声驱动参数在 “平坦区域”（泛化能力更强）附近震荡，而非收敛到 “尖锐区域”（易过拟合）。
   数学上，SGD 的噪声动力学可等效于引入一个“景观”（损失函数的高维度空间）依赖的正则化项：
   $R\propto \eta \cdot \text{Tr}\left({\nabla }^{2}L\cdot \text{Cov}(g_t)\right)$
   其中，$\text{Cov}(g_t)$是梯度噪声的协方差矩阵。该正则化项惩罚损失函数的曲率，引导模型趋向更平坦的解。
2. 学习率的全局一致性
   SGD 的固定学习率强制所有参数以相同步长更新，这在训练后期尤为重要。例如，当模型接近最优解时，Adam 的自适应学习率可能因个别参数的梯度消失而停滞，而 SGD 通过持续的全局更新维持探索能力，避免过早收敛到局部最小值。
3. 损失景观的选择偏好
   SGD 的噪声更倾向于将参数推向宽谷区域（损失函数曲率小），而 Adam 的自适应学习率可能陷入窄谷区域（曲率大但训练误差低）。实验表明，宽谷区域的解对输入扰动更不敏感，泛化性能显著优于窄谷解。例如，在 CIFAR-10 数据集上，SGD 训练的 ResNet 测试误差比 Adam 低 2% 以上。
4. 避免自适应学习率的过拟合风险
   Adam 的自适应学习率会根据训练数据动态调整每个参数的更新步长，这在小数据集上可能导致过拟合。例如，当某个参数的梯度长期为零时，Adam 会自动增大其学习率，可能放大该参数的随机波动，而 SGD 的固定学习率能抑制这种波动。

优化器选择的核心逻辑

场景	推荐优化器	原因
小批量（batch ≤ 32）	RAdam 或 SGD	RAdam 通过动态机制平衡稳定性与效率；SGD 的噪声正则项提升泛化。
大规模数据（batch ≥ 128）	Adam	二阶矩估计稳定，自适应学习率加速收敛 。
追求泛化能力	SGD+Momentum	噪声正则化引导模型趋向宽谷解，泛化性能最优。
快速实验或调参困难	RAdam	对学习率鲁棒，无需手动 warmup。

六、Lookahead

Look Ahead 是一种优化器技术，它并非独立的优化器，而是可以与其他优化器（如 Adam、SGD 等）结合使用，提升训练效果。

1. Lookahead 优化器原理
   Lookahead 采用了两阶段更新机制，包括一个快速更新器（fast optimizer）和一个慢速更新器（slow optimizer），具体步骤如下：
   • 快速更新：使用常见的优化器（如 Adam、SGD 等）作为快速更新器，在每一步训练中对参数进行快速更新。假设快速更新器在第t步更新后的参数为${\theta }_t^{\text{fast}}$ ，其更新方式遵循对应优化器的规则。例如，若快速更新器是 Adam，那么就是按照 Adam 的参数更新公式来计算 ${\theta }_t^{\text{fast}}$ 。
   • 慢速更新：每间隔k步（超参数，例如$k=5$），对慢速更新器的参数 ${\theta }_t^{\text{slow}}$ 进行更新。更新公式为：
     $${\theta }_t^{\text{slow}}=\alpha \cdot {\theta }_{t-k}^{\text{slow}}+(1-\alpha )\cdot {\theta }_t^{\text{fast}}$$
     其中，$\alpha$ 是一个介于 0 和 1 之间的超参数（通常取值约为 0.5）。这意味着慢速更新器的参数是由上一次的慢速参数和当前快速更新后的参数加权平均得到的。
   • 参数重置：将快速更新器的参数重置为慢速更新器的参数，即 ${\theta }_t^{\text{fast}}={\theta }_t^{\text{slow}}$，然后继续下一轮的快速更新。
2. Lookahead 优化器优劣势

• 优势：
  • 提升稳定性：通过慢速更新对快速更新产生的波动进行平滑，减少了参数更新过程中的噪声影响，使训练过程更加稳定，尤其在训练初期，能有效避免参数的剧烈震荡。
  • 增强泛化能力：实验表明，Lookahead 可以提升模型的泛化性能，减少过拟合现象。这是因为慢速更新的平滑机制使得模型学习到的参数更加鲁棒，不会过度拟合训练数据中的噪声。
  • 兼容性强：可以与多种不同类型的优化器结合使用，不需要对原优化器的核心算法进行大幅修改，应用起来比较灵活。
• 劣势：
  • 增加计算和调参复杂度：引入了额外的超参数k和$\alpha$，需要进行调参以找到最优的组合，增加了调参的工作量。同时，额外的更新步骤也会带来一定的计算开销。
  • 并非适用于所有场景：在一些简单任务或者数据量非常小的情况下，可能无法充分发挥其优势，甚至可能会因为额外的复杂度而导致性能下降。

3. Lookahead 优化器更稳定的原因

• 平滑参数更新路径：快速更新器在每一步都基于当前批次的数据进行参数更新，容易受到批次噪声的影响，导致参数更新路径波动较大。而慢速更新器通过加权平均的方式，综合了多步快速更新的结果，相当于对快速更新的结果进行了平滑处理，使得最终采用的参数（即慢速更新器的参数）变化更加平稳，减少了噪声对参数更新的干扰。
• 抑制过拟合倾向：过拟合往往是由于模型在训练过程中对训练数据中的噪声过度敏感，导致学到的特征过于特殊化。Lookahead 的慢速更新机制使得模型参数不会过度适应某几个批次数据的噪声，能够学习到更具一般性的特征表示，从而使训练过程更加稳定，模型在验证集上的表现也更加稳定。
• 多尺度探索：快速更新器负责在小尺度上快速探索参数空间，寻找局部较优的参数；而慢速更新器则从更大的尺度上对参数进行调整和整合。这种多尺度的参数更新方式避免了快速更新器可能陷入局部最优的问题，让模型在参数空间的搜索更加稳健，进而提升了训练的稳定性。
  

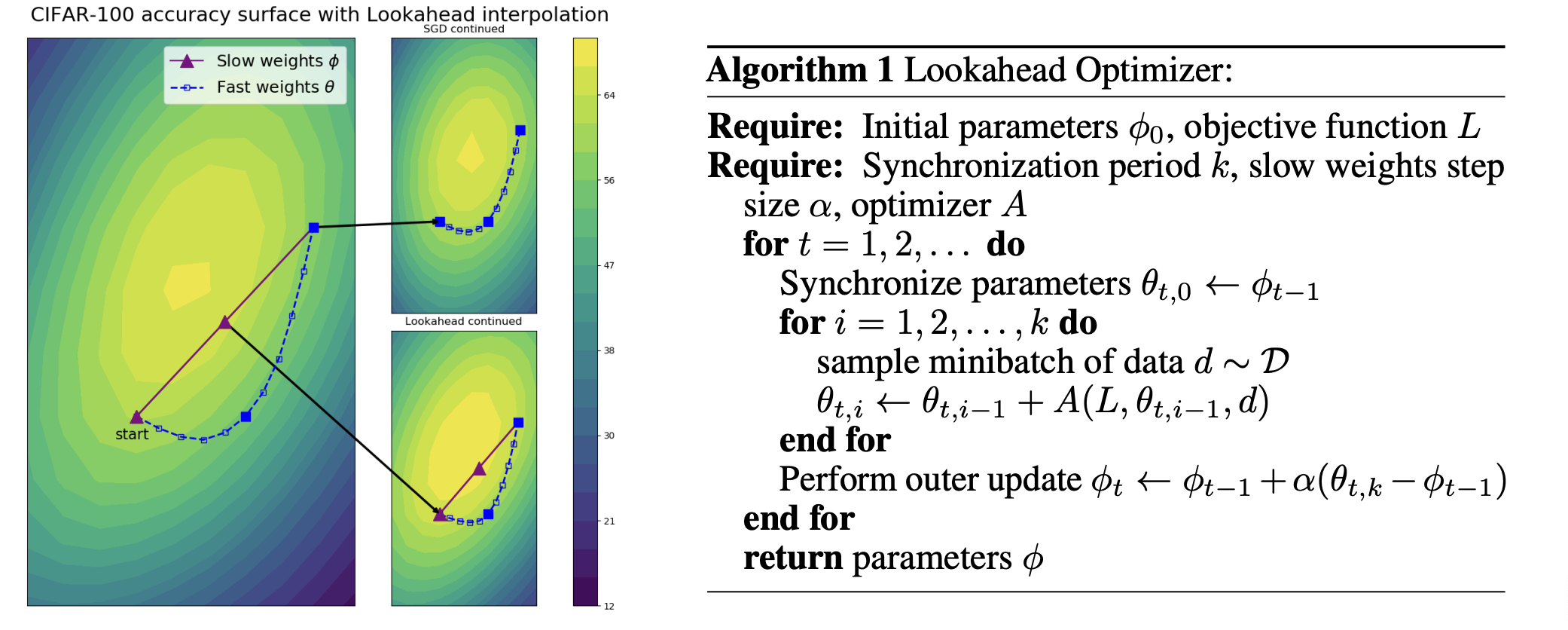
4. Lookahead 优化器直观理解
   想象在群山中，树木茂密，我们不知道怎么下山。这时有一个探索机器人（fast optimizer），根据局部梯度探索走了N步（可能绕路、反复调整方向等），然后我们可以直接根据机器人当前位置指导我们的方向，避免了我们绕路（深度模型优化中某个Batch的噪声）。我们可以朝着机器人的方向直接更新一大步，然后唤回机器人到我们位置，再次让机器人探索N步。

七、融合型优化器：Ranger

Ranger 是当前工业界表现优异的融合型优化器，由RAdam（一/二阶矩修正）+ Lookahead（两阶段更新） 组合而成，兼顾收敛速度与泛化能力。

1. 核心组件

   • RAdam：解决 Adam 的小批量偏差，动态切换更新策略（稳定时用 Adam，不稳定时用动量 SGD）；
   • Lookahead：两阶段更新机制 ——“快速更新器”（RAdam）探索参数空间，“慢速更新器” 每隔k步平滑参数（取快速参数与历史慢速参数的加权平均），增强稳定性。

   公式

   • (Lookahead 部分)快速参数（RAdam 更新）：
     $${\theta }_t^{\text{fast}}=\text{RAdam}({\theta }_{t-1}^{\text{fast}})$$
   • 慢速参数（每k步更新）：
     $$\begin{gathered} {\theta }_t^{\text{slow}}=\alpha \cdot {\theta }_{t-k}^{\text{slow}}+(1-\alpha )\cdot {\theta }_t^{\text{fast}} \\ （\alpha \approx 0.5，k\approx 5） \end{gathered}$$
   • 最终参数：${\theta }_t={\theta }_t^{\text{slow}}$（快速参数重置为慢速参数，继续探索）。

   
   核心思想

   • RAdam 保证 “高效探索”：解决小批量偏差，加速收敛；
   • Lookahead 保证 “稳健收敛”：平滑快速更新的噪声，抑制过拟合，提升泛化能力。

   
   优劣分析

   • 优点：在 ImageNet、COCO 等大规模数据集上，收敛速度优于 Adam，泛化能力接近 SGD；
   • 缺点：实现复杂度高于基础优化器，需调参（如k和$\alpha$）。

八、训练技巧：适配优化器的实用策略

优化器的性能不仅取决于自身设计，还需配合合理的训练技巧。以下策略针对不同优化器的特性设计，可显著提升训练效果。

1. 学习率调度（Learning Rate Scheduling）
   学习率是优化器的核心超参，需根据训练阶段动态调整：
   • SGD / 动量 SGD：适合 “余弦退火”（cosine annealing）或 “循环学习率”（cyclic LR），通过波动学习率跳出局部最优；
   • Adam/RAdam：适合 “线性衰减”（linear decay）或 “分段衰减”（step decay），避免自适应学习率过大导致过拟合；
   • 通用策略：ReduceLROnPlateau（当验证指标停滞时，学习率乘以 0.5），动态适配收敛瓶颈。
2. 权重初始化与正则化初始化：
   • 优化器对参数初始值敏感，需用适配激活函数的初始化方法（如 ReLU 用 He 初始化，Sigmoid 用 Xavier 初始化），避免梯度消失 / 爆炸；
   • 正则化：SGD 适合 L2 正则化（直接在梯度中加入参数项）；
   • Adam/RAdam 适合 AdamW（将 L2 改为权重衰减，避免自适应学习率削弱正则效果）。
3. 批量大小与梯度累积
   • 批量大小影响优化器稳定性：
     • SGD 在小批量（32-128）下泛化更好，Adam 在中批量（128-512）下更稳定；
   • 梯度累积（Gradient Accumulation）：当 GPU 内存有限时，用多步小批量累积梯度后更新参数（等效于增大批量），需注意学习率同步放大（如累积 4 步，学习率 ×4）。
4. 梯度裁剪（Gradient Clipping）
   当梯度爆炸时（如 RNN 训练中），需裁剪梯度范数至阈值（如$max\_norm=10$）：
   $$\text{if}\Vert \nabla L\Vert >\text{max\_norm},\nabla L=\nabla L\cdot \frac{\text{max\_norm}}{\Vert \nabla L\Vert }$$
   该策略对动量优化器（如 SGD+Momentum）和自适应优化器（如 Adam）均有效。
5. 早停与温启动
   • 早停（Early Stopping）：以验证集损失为指标，当连续N轮（如 20 轮）无提升时停止训练，避免过拟合（对 Adam 类优化器尤其重要）；
   • 温启动（Warm-up）：训练初期用小学习率（如初始$\eta =0.001$，逐步增至$\eta =0.01$），避免参数剧烈波动（适合 Transformer 等大模型，配合 Adam 使用）。
6. 优化器选择指南
   • 追求快速收敛：优先用 Adam/RAdam（适合大规模数据、高维模型）；
   • 追求强泛化能力：优先用 SGD+Momentum（适合小数据集、低维模型）；
   • 平衡两者：用 Ranger（尤其在 CV、NLP 等复杂任务中）。

九、总结

优化器的演进是 “问题驱动” 的：从解决 SGD 的震荡（动量），到适配参数差异（自适应学习率），再到修正估计偏差（RAdam），最终通过融合策略（Ranger）实现综合性能提升。实际应用中，需根据模型规模、数据特性和训练目标选择优化器，并配合学习率调度、正则化等技巧，才能高效训练出高性能模型。