【计算机组成原理】浮点数表示与运算

什么是浮点数

        浮点数是一种在计算机中表示实数的方式，起因在于定点数无法有效表示非常大或非常小的数（如 3.1415、0.0000001 或 1e+20），这在科学计算、图形处理、工程建模等领域中是常见需求。为此，引入了浮点数，它通过科学计数法的思想，用符号位、阶码和尾数的组合表示实数。

        通常，浮点数表示为：

        式中式中，S取值0或1，用来决定浮点数的符号；M是一个二进制定点小数，称为尾数，一般用定点原码（无符号）小数表示；E是一个二进制定点整数，称为阶码或指数，用移码表示。R是基数（隐含），可以约定为2、4、16等。可见浮点数由符号、尾数和阶码三部分组成。

IEEE754标准规定

        在IEEE754标准中，浮点数的格式如下：

     

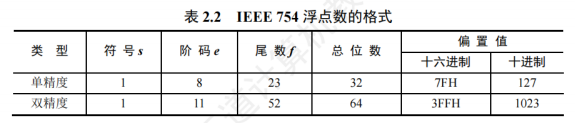
        （图源王道）

        其中尾数用无符号原码表示，移码用偏置值127或1023的移码表示。

规格化浮点数

        尾数规格化

        首先，对于尾数的规格化，要求隐含一位有效位，不能够浪费尾数的精度。

        对于IEEE754,要求小数点前隐含有效位1。例如，尾数表示为0111001实际真值为1.0111001。

        对于用补码表示的尾数，要求其转换为原码后的尾数小数点后第一位为1。例如：1.11000，转换为原码后为1.01000，其中1.01000的第一个1表示符号，此时小数点后第一个有效位为0，浪费了一位尾数精度，应该进行左规变成1.10000，同时阶码-1。

        对于用基为4的原码表示的尾数，要求其小数点后两位不能同时为0。因为基为4的尾数进行左规时，尾数应移动两位。

        阶码规格化

        对于IEEE754，要求阶码不能全为0或者全为1。、

        所以对于float型，即32位浮点数，其阶码的范围为0到扣去一个最小值和最大值，即1-254，对应真值为1-127到254-127，即-126到127

        对于double型，即64位浮点数，其阶码的范围为1到2046，对应真值为-1022到1023。

        规格化浮点数的表示范围

        显然：

        1、对于正单精度浮点数

        MAX：阶码=11111110=254，尾数=全1=，最大真值=(2-2^23)*2^127。

        MIN：阶码=00000001=1，尾数=全0=，最小真值=1*2^-126。

        由于负数与正数在数轴上关于原点对称，所以可以得到规格化单精度浮点数的表示范围为：

        

        2、双精度浮点数也适用类似的计算方法。

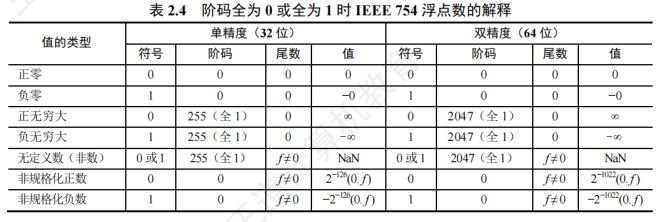
非规格化浮点数

        非规格化浮点数表示表格如下：

浮点数加减法

        浮点数加减运算的步骤如下：

        1、对阶：小阶看大阶，即把阶码小的尾数进行右移。

        2、尾数相加减：如题。

        3、规格化：进行左规或者右规，使尾数符合规格化条件（不浪费尾数精度）。

        4、舍入：0舍1入。

        5、溢出判断：看阶码是否超出范围（上下溢出）。

        PS：如果发生了上下溢出，上溢机器视为正负无穷，下溢视为机器0。若开启异常监测，则报错。

类型转换问题

        程序运行中，强转、赋值、计算过程都可能带来类型转换，从【计算机组成原理】C语言中数据类型表示及转换总结中可以知道，从短型转长型过程中不会出现任何损失，即char-short-int-long；float-doule。

       首先需要记住int为32位，float尾数为23位，double尾数为52位。其他一些特殊情况列举如下：

        1、int-float

        首先int有32位，float尾数只有23位，所以int转float时很容易发生精度损失。

        2、double-float或int

        首先尾数位数得知很有可能发生精度损失；其次double表示范围远大于float和int，会发生溢出。