量子算法导论
重学了量子算法,不知道是温故而知新,还是之前的教材没有讲过这个概念。
如果把(图灵机)计算机比作一个查询机器,输入x通过f(x)作用得出结果,而查询的过程就是计算的过程。
中文解释一下,当我们说“评估”或“查询”的过程,意味着算法需要从输入数据中获取信息。就比如输入为函数f(x)的x,来自于集合,输出f(x)属于集合
,那么这个过程就是“查询”。计算过程通过查询输入x获取 f(x) 的值。
-
查询的作用:查询是算法与输入数据之间的桥梁。每次查询都意味着算法需要从输入中读取一部分信息(例如 f(x)f(x)),这些信息会影响算法的后续操作。
-
效率的衡量:为了评估查询算法的效率,我们通常统计算法对输入的查询次数。查询次数越少,说明算法需要与输入交互的次数越少,通常意味着算法的效率越高。这是因为每次查询都可能涉及时间或资源的消耗,减少查询次数可以降低算法的整体复杂度。
量子最基础的算法是Deutsch算法,输入是长度为1的函数f,而Deutsch-Jozsa输入是长度为n的函数f,输出是判断函数是平衡的还是连续的,如果是平衡函数,即0和1的数量相同,如果是非平衡函数,那么只出现1或者0,所以对于长度为n的函数,需要多少次查询才能判断呢?

其计算过程如下,pi1和pi2,pi3对应于每一次操作后的量子态

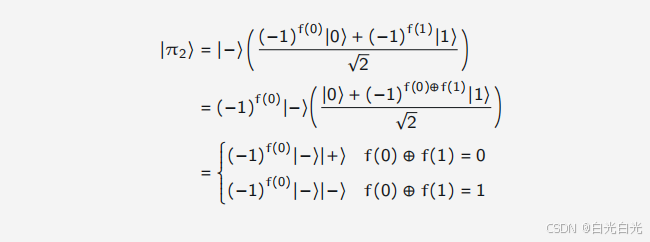




对于查询这样的问题,或许有人会问,提出这样复杂且高度人为的问题,没有人会在实践中使用它们,但是这并不意味着这个问题并不有趣,而只是模型研究的一部分,寻找揭示量子计算潜在优势的极端情况。有时,似乎认为或不自然的事情会提供意外的线索或激发新想法。shor的量子算法是由simon的算法直接启发的。
一些命名故事:
关于命名法的评论
在Bernstein-Vazirani问题的背景下,常见的是,Deutsch-Jozsa算法被称为“ Bernstein-Vazirani算法”。这有点误导,因为算法是Deutsch-Jozsa算法,正如Bernstein和Vazirani在其工作中明确指出的那样。
伯恩斯坦(Bernstein)和瓦齐拉尼(Vazirani)在表明德意志 - 乔兹萨(Deutsch-Jozsa)算法解决了伯恩斯坦 - 瓦泽拉尼(Bernstein-Vazirani)问题(如上所述)是为了定义一个更为复杂的问题,称为递归傅立叶傅立叶采样问题。这是一个高度人为的问题,解决问题的不同实例的解决方案有效地解锁了在树状结构中排列的问题的新级别。前面描述的伯恩斯坦 - 瓦泽拉尼问题本质上只是这个更复杂问题的基本案例。
这个更复杂的问题是查询问题的第一个已知示例,在该问题中,量子算法比概率算法具有所谓的超级物质优势,从而超过了量子的优势,而不是deutsch-jozsa算法提供的量子。直观地说,问题的递归版本有效地放大了 1对 n量子算法的优势对更大的东西。可以说,此分析中最困难的部分是表明经典查询算法无法在没有大量查询的情况下解决问题。这实际上是非常典型的 - 很难排除允许经典查询算法有效解决问题的创造性方法。
Simon的问题以及下一节中描述的算法确实提供了一个更简单的示例,即量子比经典算法的超级多项式(实际上是指数级)优势,因此,递归傅立叶采样问题是不太经常讨论。然而,从计算复杂性理论的角度来看,这是一个非常有趣的计算问题。
参考:
1.https://learning.quantum.ibm.com/course/fundamentals-of-quantum-algorithms/
