stack and queue 之牛刀小试

引言：学习了stack和queue的使用，现在来牛刀小试一下吧！

---

155. 最小栈 - 力扣（LeetCode）

设计一个支持 push ，pop ，top 操作，并能在常数时间内检索到最小元素的栈。
实现 MinStack 类:
• MinStack() 初始化堆栈对象。
• void push(int val) 将元素val推入堆栈。
• void pop() 删除堆栈顶部的元素。
• int top() 获取堆栈顶部的元素。
• int getMin() 获取堆栈中的最小元素。 
示例 1:
输入：
["MinStack","push","push","push","getMin","pop","top","getMin"]
[[],[-2],[0],[-3],[],[],[],[]]

输出：
[null,null,null,null,-3,null,0,-2]

解释：
MinStack minStack = new MinStack();
minStack.push(-2);
minStack.push(0);
minStack.push(-3);
minStack.getMin();   --> 返回 -3.
minStack.pop();
minStack.top();      --> 返回 0.
minStack.getMin();   --> 返回 -2.

根据我们之前亲自动手实现的栈，我们知道栈是一种操作受限的数据结构，只能从栈顶插入或弹出元素，所以对于标准的栈来说，如果想实现本题的 getMin 方法，只能老老实实把所有元素弹出来然后找最小值。想提高时间效率，那肯定要通过空间换时间的思路。
不过在具体说解法之前，我想聊一下动态集合中维护最值的问题。这类问题看似简单，但实际上是个很棘手的问题。其实本题就是如下一个场景：
假设你有若干数字，你用一个 min 变量维护了其中的最小值，如果现在给这些数字中添加一个新数字，那么只要比较这个新数字和 min 的大小就可以得出最新的最小值。但如果现在从这些数字钟删除一个数字，你还能用 min 变量得到最小值吗？答案是不能，因为如果这个被删除的数字恰好是最小值，那么新的 min 变量应该更新为第二小的元素对吧，但是我没有记录第二小的元素是多少，所以只能把所有数字重新遍历一遍。
明确了难点再回到本题，就可以对症下药了。删除栈顶元素的时候，不确定新的最小值是多少，但楼下那哥们知道啊，他当时入栈时的最小值，就是现在的最小值呗。
所以这道题的关键就是，每个元素入栈时，还要记下来当前栈中的最小值。比方说，可以用一个额外的栈 minStk 来记录栈中每个元素入栈时的栈中的最小元素是多少，这样每次删除元素时就能快速得到剩余栈中的最小元素了。

class MinStack {
public:MinStack() {}     void push(int val) {_st.push(val);if(_minst.empty()||val <= _minst.top())_minst.push(val);}void pop() {if(_minst.top() == _st.top())_minst.pop();_st.pop();}int top() {return _st.top();}int getMin() {return _minst.top();}private:stack<int> _st;stack<int> _minst;};/*** Your MinStack object will be instantiated and called as such:* MinStack* obj = new MinStack();* obj->push(val);* obj->pop();* int param_3 = obj->top();* int param_4 = obj->getMin();*/

---

 栈的压入、弹出序列_牛客题霸_牛客网

描述

输入两个整数序列，第一个序列表示栈的压入顺序，请判断第二个序列是否可能为该栈的弹出顺序。假设压入栈的所有数字均不相等。例如序列1,2,3,4,5是某栈的压入顺序，序列4,5,3,2,1是该压栈序列对应的一个弹出序列，但4,3,5,1,2就不可能是该压栈序列的弹出序列。

1. 0<=pushV.length == popV.length <=1000

2. -1000<=pushV[i]<=1000

3. pushV 的所有数字均不相同

示例1

输入：

[1,2,3,4,5],[4,5,3,2,1]返回值：true说明：可以通过push(1)=>push(2)=>push(3)=>push(4)=>pop()=>push(5)=>pop()=>pop()=>pop()=>pop()
这样的顺序得到[4,5,3,2,1]这个序列，返回true      

示例2

输入：

[1,2,3,4,5],[4,3,5,1,2]
返回值：false
说明：由于是[1,2,3,4,5]的压入顺序，[4,3,5,1,2]的弹出顺序，要求4，3，5必须在1，2前压入，且1，2不能弹出，但是这样压入的顺序，1又不能在2之前弹出，所以无法形成的，返回false      

class Solution {
public:/*** 代码中的类名、方法名、参数名已经指定，请勿修改，直接返回方法规定的值即可** * @param pushV int整型vector * @param popV int整型vector * @return bool布尔型*/bool IsPopOrder(vector<int>& pushV, vector<int>& popV) {stack<int> st;int pushi = 0,popi = 0;while(pushi < pushV.size()){st.push(pushV[pushi++]);while(!st.empty() && st.top() == popV[popi]){st.pop();popi++;}}return st.empty();}
};

---

 150. 逆波兰表达式求值 - 力扣（LeetCode）

给你一个字符串数组 tokens ，表示一个根据 逆波兰表示法 表示的算术表达式。

请你计算该表达式。返回一个表示表达式值的整数。

注意：

• 有效的算符为 '+'、'-'、'*' 和 '/' 。
• 每个操作数（运算对象）都可以是一个整数或者另一个表达式。
• 两个整数之间的除法总是 向零截断 。
• 表达式中不含除零运算。
• 输入是一个根据逆波兰表示法表示的算术表达式。
• 答案及所有中间计算结果可以用 32 位 整数表示。

示例 1：

输入：tokens = ["2","1","+","3","*"]
输出：9
解释：该算式转化为常见的中缀算术表达式为：((2 + 1) * 3) = 9

示例 2：

输入：tokens = ["4","13","5","/","+"]
输出：6
解释：该算式转化为常见的中缀算术表达式为：(4 + (13 / 5)) = 6

示例 3：

输入：tokens = ["10","6","9","3","+","-11","*","/","*","17","+","5","+"]
输出：22
解释：该算式转化为常见的中缀算术表达式为：((10 * (6 / ((9 + 3) * -11))) + 17) + 5
= ((10 * (6 / (12 * -11))) + 17) + 5
= ((10 * (6 / -132)) + 17) + 5
= ((10 * 0) + 17) + 5
= (0 + 17) + 5
= 17 + 5
= 22

逆波兰表达式发明出来就是为了方便计算机运用「栈」进行表达式运算的，其运算规则如下：
按顺序遍历逆波兰表达式中的字符，如果是数字，则放入栈；如果是运算符，则将栈顶的两个元素拿出来进行运算，再将结果放入栈。对于减法和除法，运算顺序别搞反了，栈顶第二个数是被除（减）数。
所以这题很简单，直接按照运算规则借助栈计算表达式结果即可。 

class Solution {
public:int evalRPN(vector<string>& tokens) {stack<int> s;for (size_t i = 0; i < tokens.size(); ++i){string& str = tokens[i];// str为数字if (!("+" == str || "-" == str || "*" == str || "/" == str)){s.push(atoi(str.c_str()));}else{// str为操作符int right = s.top();s.pop();int left = s.top();s.pop();switch (str[0]){case '+':s.push(left + right);break;case '-':s.push(left - right);break;case '*':s.push(left * right);break;case '/':// 题目说明了不存在除数为0的情况s.push(left / right);break;}}}return s.top();}
};

---

232. 用栈实现队列 - 力扣（LeetCode）

 请你仅使用两个栈实现先入先出队列。队列应当支持一般队列支持的所有操作（push、pop、peek、empty）：

实现 MyQueue 类：

• void push(int x) 将元素 x 推到队列的末尾
• int pop() 从队列的开头移除并返回元素
• int peek() 返回队列开头的元素
• boolean empty() 如果队列为空，返回 true ；否则，返回 false

说明：

• 你 只能 使用标准的栈操作 —— 也就是只有 push to top, peek/pop from top, size, 和 is empty 操作是合法的。
• 你所使用的语言也许不支持栈。你可以使用 list 或者 deque（双端队列）来模拟一个栈，只要是标准的栈操作即可。

示例 1：

输入：
["MyQueue", "push", "push", "peek", "pop", "empty"]
[[], [1], [2], [], [], []]
输出：
[null, null, null, 1, 1, false]解释：
MyQueue myQueue = new MyQueue();
myQueue.push(1); // queue is: [1]
myQueue.push(2); // queue is: [1, 2] (leftmost is front of the queue)
myQueue.peek(); // return 1
myQueue.pop(); // return 1, queue is [2]
myQueue.empty(); // return false

对于一个正常的的队列，它的 pop/push 等方法都是 O(1) 的复杂度。如果题目非要让我们用栈的 API 模拟队列的 API 肯定可以做到，但复杂度肯定会高一些。
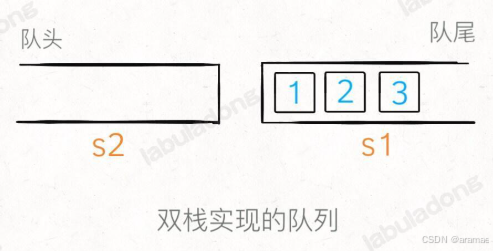
最简单的一个思路，我们使用两个栈 s1, s2 就能实现一个队列的功能。
当调用 push 让元素入队时，只要把元素压入 s1 即可，时间复杂度 O(1)：

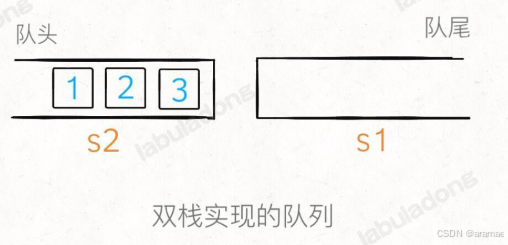
使用 peek 或 pop 操作队头的元素时，若 s2 为空，可以把 s1的所有元素取出再添加进 s2，这时候 s2 中元素就是先进先出顺序了，不过这样移动所有元素的复杂度是 O(n)：

class MyQueue {
private:stack<int> s1, s2;public:MyQueue() {// Constructor initializes two stacks}// 添加元素到队尾void push(int x) {s1.push(x);}// 删除队头元素并返回int pop() {// 先调用 peek 保证 s2 非空peek();int topElement = s2.top();s2.pop();return topElement;}// 返回队头元素int peek() {if (s2.empty()) {// 把 s1 元素压入 s2while (!s1.empty()) {s2.push(s1.top());s1.pop();}}return s2.top();}// 判断队列是否为空bool empty() {return s1.empty() && s2.empty();}
};

---

225. 用队列实现栈 - 力扣（LeetCode）

请你仅使用两个队列实现一个后入先出（LIFO）的栈，并支持普通栈的全部四种操作（push、top、pop 和 empty）。

实现 MyStack 类：

• void push(int x) 将元素 x 压入栈顶。
• int pop() 移除并返回栈顶元素。
• int top() 返回栈顶元素。
• boolean empty() 如果栈是空的，返回 true ；否则，返回 false 。

注意：

• 你只能使用队列的标准操作 —— 也就是 push to back、peek/pop from front、size 和 is empty 这些操作。
• 你所使用的语言也许不支持队列。 你可以使用 list （列表）或者 deque（双端队列）来模拟一个队列 , 只要是标准的队列操作即可。

示例：

输入：
["MyStack", "push", "push", "top", "pop", "empty"]
[[], [1], [2], [], [], []]
输出：
[null, null, null, 2, 2, false]解释：
MyStack myStack = new MyStack();
myStack.push(1);
myStack.push(2);
myStack.top(); // 返回 2
myStack.pop(); // 返回 2
myStack.empty(); // 返回 False

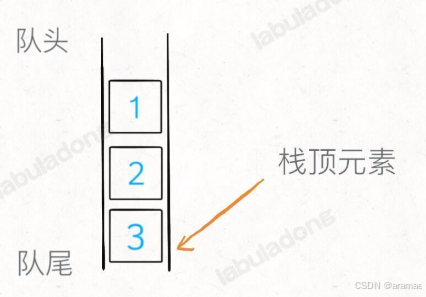
底层用队列实现栈就比较简单粗暴了，只需要一个队列作为底层数据结构。
底层队列只能向队尾添加元素，所以栈的 pop API 相当于要从队尾取元素：

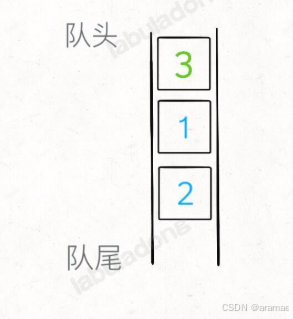
那么最简单的思路就是，把队尾元素前面的所有元素重新塞到队尾，让队尾元素排到队头，这样就可以取出了： 

class MyStack {queue<int> q;int top_elem = 0;public:// 将元素 x 压入栈顶void push(int x) {// x 是队列的队尾，是栈的栈顶q.push(x);top_elem = x;}// 返回栈顶元素int top() {return top_elem;}// 删除栈顶的元素并返回int pop() {int size = q.size();// 留下队尾 2 个元素while (size > 2) {q.push(q.front());q.pop();size--;}// 记录新的队尾元素top_elem = q.front();q.push(q.front());q.pop();// 删除之前的队尾元素int result = q.front();q.pop();return result;}// 判断栈是否为空bool empty() {return q.empty();}
};

---

 215. 数组中的第K个最大元素 - 力扣（LeetCode）

给定整数数组 nums 和整数 k，请返回数组中第 k 个最大的元素。

请注意，你需要找的是数组排序后的第 k 个最大的元素，而不是第 k 个不同的元素。

你必须设计并实现时间复杂度为 O(n) 的算法解决此问题。

示例 1:

输入: [3,2,1,5,6,4], k = 2
输出: 5

示例 2:

输入: [3,2,3,1,2,4,5,5,6], k = 4
输出: 4

提示：

• 1 <= k <= nums.length <= 105
• -104 <= nums[i] <= 104

 这里采用二叉堆的解法，可以把小顶堆 pq 理解成一个筛子，较大的元素会沉淀下去，较小的元素会浮上来；当堆大小超过 k 的时候，我们就删掉堆顶的元素，因为这些元素比较小，而我们想要的是前 k 个最大元素嘛。

当 nums 中的所有元素都过了一遍之后，筛子里面留下的就是最大的 k 个元素，而堆顶元素是堆中最小的元素，也就是「第 k 个最大的元素」。

二叉堆插入和删除的时间复杂度和堆中的元素个数有关，在这里我们堆的大小不会超过 k，所以插入和删除元素的复杂度是 O(logK)，再套一层 for 循环，总的时间复杂度就是 O(NlogK)。

#include <queue>
#include <vector>class Solution {
public:int findKthLargest(std::vector<int>& nums, int k) {// 小顶堆，堆顶是最小元素std::priority_queue<int, std::vector<int>, std::greater<int>> pq;for (int e : nums) {// 每个元素都要过一遍二叉堆pq.push(e);// 堆中元素多于 k 个时，删除堆顶元素if (pq.size() > k) {pq.pop();}}// pq 中剩下的是 nums 中 k 个最大元素，// 堆顶是最小的那个，即第 k 个最大元素return pq.top();}
};