数据结构入门 (二)：挣脱连续空间的束缚 —— 单向链表详解

@TOC(目录)

引言：整齐的代价

在上一篇文章中，我们一起探索了数据结构大家族的第一位成员——顺序表。我们了解到，顺序表作为一种线性结构，其最大的特点在于逻辑顺序与物理顺序的一致性，即元素之间不仅存在逻辑上的前后关系，在物理存储空间中也以连续的方式存放。

这种“整齐”带来了显而易见的好处，比如我们可以通过索引值快速定位到任何一个元素，就像报出房间号就能立刻找到人一样。但是，凡事有利也有弊。这种对连续空间近乎苛刻的要求，也给它带来了麻烦。

图1

如图1，左边是我们的内存空间，右边是待存储的顺序表。虽然内存空闲的总空间绰绰有余，但我们却找不到一块足够大且连续的区域来放置这个顺序表。这就是顺序表的局限性之一：对连续空间要求高，容易导致空间浪费。

那么，有没有一种方法，可以解决这个问题呢？我们很容易就能想到：如果我们能让数据元素“见缝插针”，不考虑相邻位置，哪里有空位就插一个，这样不就能充分利用空间了吗？然后用一根“线”把它们按逻辑串起来，不就能完美解决这个问题了吗？

至此，我们已经初窥链表，相比起顺序表，它的组织形式更加灵活、自由。

一、温故知新：顺序表的“双刃剑”

在探讨链表之前，我们再总结一下“顺序表”的优缺点。

核心优点

• 随机访问效率高: 存储空间连续，可以通过索引直接定位元素，时间复杂度为O(1)。
• 缓存友好: 连续的内存布局对CPU缓存更友好，遍历速度通常更快。

核心痛点

• 操作成本高（时间维度）: 为了维持物理上的连续性，在中间插入或删除一个元素后，需要移动大量后续元素，时间复杂度为 O(n)。这就像队伍中间插进一个人，后面所有人都得挪一步。且数据量越大，成本就越高。
• 空间限制大（空间维度）:
  • 必须预分配: 数组通常需要预先分配固定大小的空间。如果空间小了，需要经历一个“申请新空间 -> 复制全部数据 -> 释放旧空间”的昂贵扩容过程。
  • 容易浪费或失败: 如果空间大了，则造成内存浪费。更糟糕的是，如引言所述，在内存碎片化的情况下，即使总空间足够，也可能因找不到足够大的连续块而申请失败。

二、链式存储结构：一次聪明的“解耦”

既然顺序表的“物理连续”带来了诸多不便，我们何不换个思路？那便是将元素的‘逻辑顺序’与它们的‘物理位置’彻底解耦。这正是链表设计的核心思想：它放弃了对物理连续的执着，转而选择利用物理上不连续的空间，来表示逻辑上的连续。

1.链表的“细胞”——节点

与顺序结构不同，链式结构中引入了它的基本单元——节点。每个节点除了要存储数据元素信息外，还要存储它的后继元素的存储地址。它的节点包含两部分：

1. 数据域：存储数据元素信息。
2. 指针域：存储下一个节点的内存地址。

图2.链表节点结构示例图

这里给出链表节点结构的定义：

typedef int Element_t;typedef struct _node {Element_t val;  // 数据域struct _node *next;  // 指针域
} node_t;

2.”节点“成“链”

有了节点这个基本单元，我们就可以把它们串联起来了。将所有节点链结成一个链表，这就是线性表的链式存储结构，因为此链表的每个节点只包含一个指针域，所以叫做单链表。

对于线性表来说，它一定有头也有尾。一般而言，我们会设定一个特殊的指针，它永远指向链表的第一个节点，我们叫它头指针。有时为了方便，我们会在单链表的第一个节点前添加一个节点，称为头节点。使用头节点的情况下，头指针指向的就是这个头节点，而不是第一个实际存储数据的节点。头节点的指针域存储指向第一个节点的指针，数据域可以不存储信息，也可以存储如线性表长度等附加信息。单链表的最后一个节点，指针域通常指向NULL或者None，也就是“空”。

图3.带头节点的单向链表

图4.带头指针的单向链表

3.头指针 vs 头结点

特性	头指针	头节点
本质	一个指针变量	一个实际的节点对象
空表示	head == NULL	head->next == NULL
用途	标识链表的起始位置	简化插入/删除操作
插入/删除	对第一个节点的操作是特殊的，需改动头指针本身	所有位置的操作逻辑完全统一
优点	节省一个节点的内存	代码逻辑更简单、健壮，不易出错
缺点	增删逻辑复杂，需特殊判断	增加了一个节点的内存开销
是否必要	是	否

结论：在工程实践中，为了代码的简洁和鲁棒性，强烈推荐使用带头结点的链表。这点微小的空间牺牲是完全值得的。接下来的所有操作，我们都将基于带头结点的链表进行。

为了更好地管理链表，我们通常会再封装一个结构体来代表整个链表：

// 定义链表头结构
typedef struct {node_t head;  // 头节点int count;  // 当前链表中有效数据节点的数量
} LinkList_t;

三、链表的基本功：核心操作详解

现在，让我们基于带头结点的链表 LinkList_t，来实现它的核心功能。

1.定义链表结构

链表的结构在第二部分已有说明，这里给出完整版：

typedef int Element_t;
// 1.定义链表节点结构
typedef struct _node {Element_t val;struct _node *next;
} node_t;// 2。定义链表头结构
typedef struct {node_t head;int count;
} LinkList_t;

2.创建链表

首先，我们需要一个函数来创建一个空的链表。这包括为 LinkList_t 结构体分配内存，并初始化其内部的头结点和计数器。

LinkList_t *createLinkList()
{// 1. 声明一个指向LinkList_t的指针变量table，并初始化为NULL，防止野指针。LinkList_t *table = NULL;// 2. 在堆上申请一块大小为`sizeof(LinkList_t)`的内存空间，将内存地址赋值给`table`。table = malloc(sizeof(LinkList_t));if (table == NULL)  {return NULL;   }// 3. 初始化链表结构体成员table->head.val = 0;table->head.next = NULL;table->count = 0;return table;
}

3.遍历链表

由于链表物理上不连续，我们无法随机访问。唯一的办法就是“顺藤摸瓜”：从头节点开始，沿着next指针一路走下去，直到遇到NULL。

void showLinkList(const LinkList_t* table)
{node_t *p = table->head.next; // 头节点的下一个节点，也就是链表中第一个有效数据节点的指针，将p初始化为这个节点，作为遍历的起点printf("link list:%d\n",table->count);while (p) {printf("%d\n",p->val); // 访问当前节点的数据p = p->next; // 更新p为后继节点}printf("\n"); // 打印换行符，使输出更整洁
}

4.插入节点

插入新节点有四个步骤：

1. 引入一个辅助指针*p，p找到待插入位置的前一个位置的节点。
2. 创建新节点。
3. 更新新节点。
4. 最后更新老节点。

插入操作详解

头插入（时间复杂度 O(1)）

• 头指针

  

图5.带头指针的单向链表的头插入示例图 操作步骤：

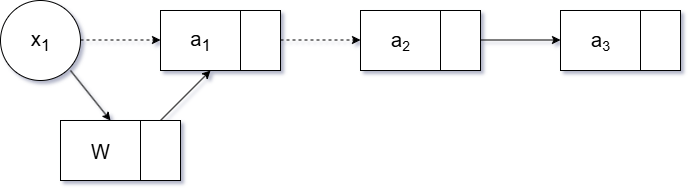
1. 新节点直接指向原头节点 x1
2. 更新头指针 x1 指向新节点

new_node->next = x1;
x1 = new_node;

• 头节点

  

图6.带头节点的单向链表的头插入示例图 操作步骤：

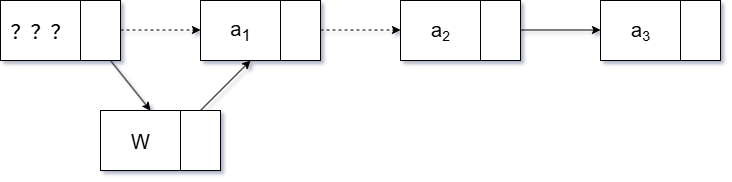
1. 新节点指向头节点的下一个节点
2. 头节点指向新节点

new_node->next = p->next;
p->next = new_node;

优势： 头插入是最高效的操作，时间复杂度恒为 O(1)，无需遍历链表

任意位置插入（时间复杂度 O(n)）

图7.单向链表任意位置插入示例图

这个指针修改动作本身是O(1)的，这正是链表效率高的原因。当然，找到这个p节点需要遍历，耗时 O(n)。链表插入的精髓就在于这两句指针操作：

new_node->next = p->next;
p->next = new_node;

这两句代码的顺序是绝对不能调换的。

解读这两句代码，可以看出是先把p的后继节点改成新节点的后继节点，再把新节点变成p的后继节点。

如果把两句代码交换一下顺序，会怎么样？

第一句将p->next覆盖成new_node的地址了。第二句new_node->next = p->next就相当于new_node->next = new_node，链表断裂了。

尾插入（时间复杂度 O(n)）

图7.单向链表尾插入示例图

p->next = new_node;                   
new_node->next = NULL;   

C语言完整实现

头插法

int insertLinkListHeader(LinkList_t* table, Element_t val)
{node_t *p = &table->head;  // p指针指向头节点node_t *new_node = malloc(sizeof(node_t));  // 创建新节点if (new_node == NULL)return -1;new_node->val = val;new_node->next = p->next;p->next = new_node;++table->count;return 0;
}

任意位置插入

int insertLinkListPos (LinkList* table, int pos, Element_t val)
{// 1.判断边界值if (pos < 0 || pos > table->count){printf("insert invalid!\n");return -1;}// 2.找到插入位置的前驱节点node_t *p = &table->head;int index = -1;while (index < pos - 1){p = p->next;index++;}if (p == NULL) {return -1;}// 3.创建新节点node_t *new_node = malloc(sizeof(node_t));new_node->val = val;// 4.插入新节点new_node->next = p->next;p->next = new_node;// 5.更新链表长度table->count++;return 0;
}

5.按值删除节点

当我们要删除某个节点时：

1. 引入辅助指针p，p找到待删除位置的前一个位置

2. 引入辅助指针备份待删除位置tmp

tmp = p->next;
p->next = tmp->next;
free(tmp);

图8.单向链删除节点示例图

int deleteLinkListElement(LinkList_t* table, Element_t val)
{node_t *p = &table->head;while (p->next){if (p->next->val == val){break;}p = p->next;}if (p->next == NULL){printf("Not Found!\n");return -1;}node_t *tmp = p->next;p->next = tmp->next;free(tmp);table->count--;return 0;
}

6.销毁链表

由于链表是节点和节点串联起来的，当销毁链表时，也需要逐个节点释放内存，最后再释放链表管理结构体本身的内存。

void releaseLinkList(LinkList_t* table)
{if (table){// 循环删除每个节点node_t *p = &table->head;node_t *tmp; // 临时保存要释放的节点while (p->next){tmp = p->next;p->next = tmp->next;free(tmp);--table->count;}printf("LinkList have %d node!\n",table->count);free(table);}
}

四、顺序表 vs. 单向链表

特性	顺序表	单向链表
存储方式	物理连续	物理离散
访问方式	随机访问 (O(1))	顺序访问 (O(n))
插入/删除	效率低，需移动元素 (O(n))	效率高，只需修改指针 (O(1)) (不含查找)
空间管理	预分配，易浪费或需扩容	按需分配，灵活，但有指针额外开销
适用场景	数据量固定，频繁查找，很少增删	数据量不固定，频繁增删，不关心随机访问

五、总结

今天，我们深入了解了单向链表。它通过牺牲随机访问的能力，换来了极其灵活的插入、删除操作和高效的空间利用率。它与顺序表并非“谁取代谁”的关系，不能简单地说哪个好，哪个不好，需要根据实际情况来选择。

掌握链表的关键，在于理解“指针”或“引用”如何将离散的内存串联成一个逻辑整体。

但是，单向链表也并非完美。我们顺着它只能一路向前，无法回头，这在某些场景下非常不便。而且，它尾部节点的next指针永远指向NULL，是不是有点“浪费”呢？

下一篇，我们将探索功能更强大的单向循环链表。同时，我们将尝试仅使用头指针来管理链表。