排序算法—交换排序(冒泡、快速)(动图演示)
目录
十大排序算法分类编辑
冒泡排序
算法步骤:
动图演示:
性能分析:
代码实现(Java):
快速排序(挖坑法)
算法步骤:
动图演示:
性能分析:
代码实现(Java):
十大排序算法分类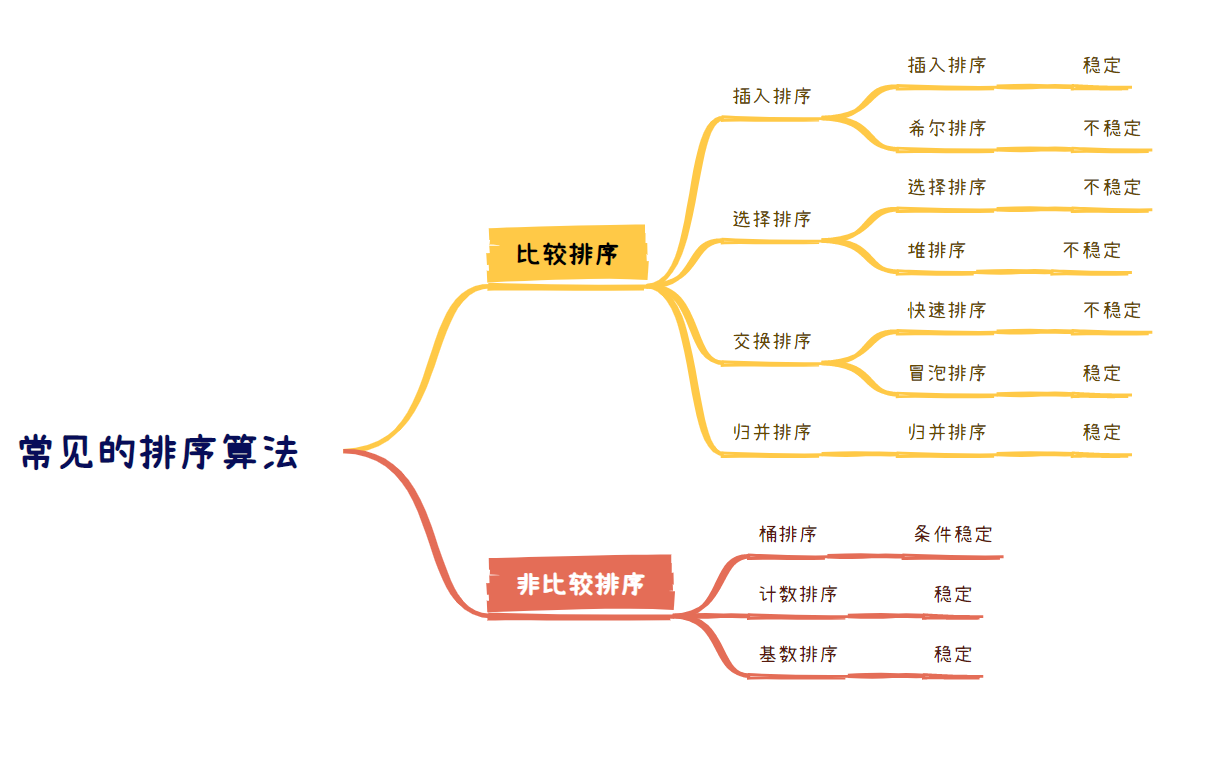
本篇分享十大排序算法中的 需要进行交换操作的冒泡排序与快速排序 , 其余算法也有介绍噢(努力赶进度中,后续会添加上)
冒泡排序
冒泡排序是一种非常直观的排序算法,遍历数组,每次比较两个元素,如果后者比前者小则交换位置 ,重复的进行直至没有再需要交换,说明该数组排序完成。冒泡排序的 名字由来是因为越小的元素会经过交换慢慢"浮"到数组的顶端。
算法步骤:
核心逻辑
- 外层循环控制轮数,共进行
n-1轮遍历,n为数组长度。- 每轮内层循环比较相邻元素
arr[j]和arr[j+1],若前者较大则交换。- 每轮结束后,当前未排序部分的最大值会“冒泡”到正确位置(数组末尾)。
优化方法
- 提前终止:引入boolean变量,如果在某轮内循环未发生交换,说明数组有序,可直接结束排序
- 减少遍历范围:每轮外层循环后,数组末尾已有序,内层循环无需再比较已排序部分。
终止条件
- 外层循环完成n - 1次遍历,或boolean = false
动图演示:
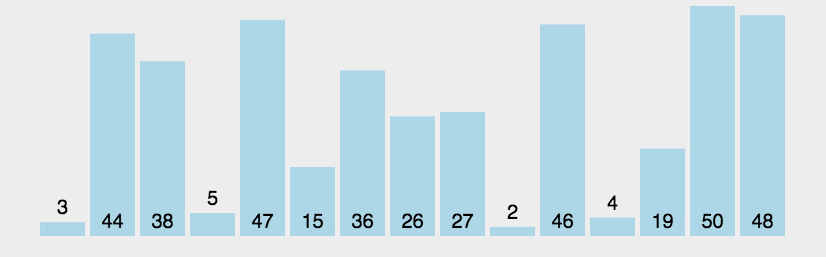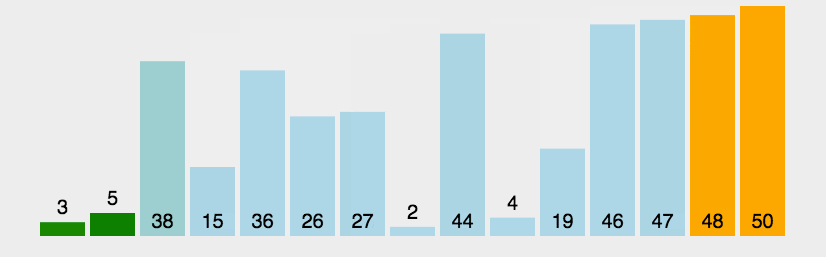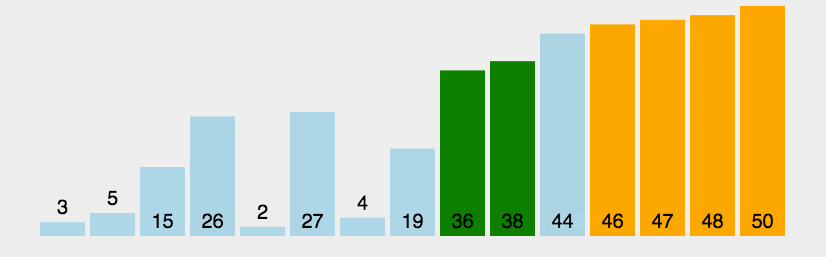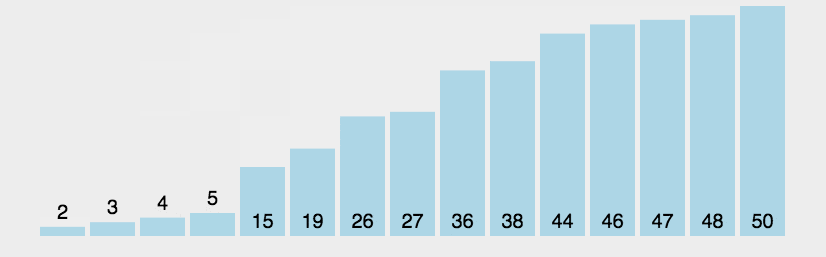
性能分析:
时间复杂度:
- 最好情况:数组已经有序,此时只需要遍历一次,时间复杂度 O(n)
- 最坏情况:数组完全倒序,此时需要遍历n - 1次,每次遍历都需要进行n - i 次 比较可能的交换(i为当前遍历次数),因此时间复杂度为O(n^2)
- 平均情况:时间复杂度为O(n^2)
空间复杂度:
- 仅需常数级额外空间 因此空间复杂度为O(1)
稳定性:
稳定排序(相等元素不会交换位置)
代码实现(Java):
/*** 冒泡排序算法实现(升序排序)* @param arr 待排序的整型数组*/
public void bubbleSort(int[] arr) {// 获取数组长度int n = arr.length;// 布尔变量用于 boolean swapped;// 外层循环:控制排序轮数(最多需要 n-1 轮)for (int i = 0; i < n - 1; i++) {// 每轮开始前初始化交换标志为 falseswapped = false;// 内层循环:比较相邻元素并交换// 每轮结束后,最大的元素会"冒泡"到数组末尾,所以比较范围逐渐缩小for (int j = 0; j < n - i - 1; j++) {// 如果前一个元素大于后一个元素(升序排序)if (arr[j] > arr[j + 1]) {// 交换相邻元素int temp = arr[j];arr[j] = arr[j + 1];arr[j + 1] = temp;// 标记发生了交换swapped = true;}}// 优化:如果本轮没有发生任何交换,说明数组已经有序,提前结束排序if (!swapped) {break;}}
}快速排序(挖坑法)
快速排序核心就是选择一个基准值(就是一个作参照的数),然后将数组分成左右两部分,左边是比基准值小的元素。右边是比基准值大的元素。 然后递归地对左右两部分继续进行这个过程,最终整个数组有序
快速排序是通过一次分区就定位一个元素的最终位置,并递归处理两侧子数组
算法步骤:
核心逻辑
- 首先设定一个基准值 (通常是第一个数字/最后一个数字),通过该基准值将数组分成左右两部分。
分区(partition):将所有小于基准值的元素移到基准值左边,大于的移到右边
递归排序:对左右两个子数组递归进行上述过程
- 概括来说为 挖坑填数 + 分治法
优化方法
- 采用三数取中法(取左、中、右三个位置的中间值作为基准值)
- 如果分区后子数组长度小于阈值(如 10)时,直接改用插入排序,减少了递归的开销
终止条件
- 当left >= right (起始索引大于等于结束索引,子数据长度 <= 1),终止当前递归(说明该子数组已有序)
- 所有子数组均完成分区和排序时,整个数组即有序
动图演示:
(借用大佬的动图)

性能分析:
时间复杂度:
- 时间性能你取决于递归的深度
- 最好情况:二叉树几乎平衡时,也就是数组划分的比较均匀(基准值位于中间)。,递归次数最少,要log2N 次。递归过程中需要对i,j下标一起扫描数组,所以总体时间复杂度时O(N*log2N)
- 最坏情况:二叉树极度不平衡 ,整体时间复杂度达到 (N²)
空间复杂度:
- 空间性能取决于递归消耗的栈空间
- 最好情况:已经分析过,需要递归logzN次,空间复杂度为O(logzN)
- 最坏情况:已经分析过,需要递归N-1次,空间复杂度为O(N)
稳定性:
- 不稳定
代码实现(Java):
public static void quickSort(int[] array) {quick(array, 0, array.length - 1);}private static void quick(int[] array, int start, int end) {// 取大于号,防止 start > endif (start >= end) {return;}int pivot = pirtiton1(array, start, end);quick(array, start, pivot - 1);quick(array, pivot + 1, end);}// 挖坑法private static int pirtiton1(int[] array, int left, int right) {int tmp = array[left];while (left < right) {// 为什么判断条件加等号,// 用int[] arr = {5, 7, 3, 1, 4, 9, 6, 5}测试while (left < right && array[right] >= tmp) {right--;}array[left] = array[right];while (left < right && array[left] <= tmp) {left++;}// 将找到的大于基准值的元素填入右边的"坑"array[right] = array[left];}// 将基准值放入最后的"坑"中(此时left == right)array[left] = tmp;return left;}
