当前位置：首页 > news >正文

【动归解题套路框架】【带备忘录的递归】【最优子结构】【自下而上DP table】

news 2025/7/17 8:13:28

动归解题套路框架

前情提要：树的遍历框架

二叉树、多叉树的遍历是递归与动态规划的基础，二者的遍历框架存在密切关联，以下先明确核心遍历逻辑。

1. 树的结构定义

二叉树节点

class TreeNode {
public:int val;TreeNode* left;  // 左子节点TreeNode* right; // 右子节点TreeNode(int v) : val(v), left(nullptr), right(nullptr) {}
};

多叉树节点

class Node {
public:int val;std::vector<Node*> children;  // 子节点列表
};

森林

森林是多棵多叉树的集合，可用根节点列表表示：

std::vector<TreeNode*> forest;  // 森林由多棵树的根节点组成

遍历森林只需对每个根节点分别执行DFS/BFS即可。

2. 深度优先遍历（DFS）框架

二叉树的DFS遍历

void traverse(TreeNode* root) {if (root == nullptr) {return;}// 前序位置：刚进入当前节点时执行traverse(root->left);  // 遍历左子树// 中序位置：左子树遍历完毕后执行（仅二叉树有）traverse(root->right); // 遍历右子树// 后序位置：右子树遍历完毕后执行
}

多叉树的DFS遍历

多叉树无中序位置（子节点数量不固定），仅保留前序和后序：

void traverse(Node* root) {if (root == nullptr) {return;}// 前序位置：刚进入当前节点时执行for (Node* child : root->children) {  // 遍历所有子节点traverse(child);}// 后序位置：所有子节点遍历完毕后执行
}

3. 广度优先遍历（层序遍历）框架

层序遍历通过队列实现，核心是按层级依次访问节点。以下分别给出二叉树和多叉树的三种层序遍历写法。

二叉树的层序遍历

写法一：基础版（无法记录节点深度）

void levelOrderTraverse(TreeNode* root) {if (root == nullptr) {return;}std::queue<TreeNode*> q;q.push(root);  // 根节点入队while (!q.empty()) {TreeNode* cur = q.front();q.pop();// 访问当前节点std::cout << cur->val << std::endl;// 左、右子节点入队if (cur->left != nullptr) q.push(cur->left);if (cur->right != nullptr) q.push(cur->right);}
}

写法二：记录节点深度（通过层级循环控制）

void levelOrderTraverse(TreeNode* root) {if (root == nullptr) {return;}std::queue<TreeNode*> q;q.push(root);int depth = 1;  // 根节点视为第1层while (!q.empty()) {int sz = q.size();  // 当前层节点数量// 遍历当前层所有节点for (int i = 0; i < sz; ++i) {TreeNode* cur = q.front();q.pop();// 访问当前节点，附带深度信息std::cout << "depth = " << depth << ", val = " << cur->val << std::endl;// 左、右子节点入队if (cur->left != nullptr) q.push(cur->left);if (cur->right != nullptr) q.push(cur->right);}depth++;  // 当前层遍历完毕，深度+1}
}

写法三：通过状态类记录深度（适配复杂场景）

// 状态类：记录节点及对应深度
class State {
public:TreeNode* node;int depth;State(TreeNode* n, int d) : node(n), depth(d) {}
};void levelOrderTraverse(TreeNode* root) {if (root == nullptr) {return;}std::queue<State> q;q.push(State(root, 1));  // 根节点深度为1while (!q.empty()) {State state = q.front();q.pop();TreeNode* cur = state.node;int depth = state.depth;// 访问当前节点，附带深度信息std::cout << "depth = " << depth << ", val = " << cur->val << std::endl;// 左、右子节点入队，深度+1if (cur->left != nullptr) q.push(State(cur->left, depth + 1));if (cur->right != nullptr) q.push(State(cur->right, depth + 1));}
}

多叉树的层序遍历

多叉树的层序遍历与二叉树逻辑一致，仅将“左右子节点”替换为“所有子节点”。

写法一：基础版（无深度记录）

void levelOrderTraverse(Node* root) {if (root == nullptr) {return;}std::queue<Node*> q;q.push(root);while (!q.empty()) {Node* cur = q.front();q.pop();// 访问当前节点std::cout << cur->val << std::endl;// 所有子节点入队for (Node* child : cur->children) {q.push(child);}}
}

写法二：记录节点深度（层级循环控制）

#include <iostream>
#include <queue>
#include <vector>void levelOrderTraverse(Node* root) {if (root == nullptr) {return;}std::queue<Node*> q;q.push(root);int depth = 1;  // 根节点视为第1层while (!q.empty()) {int sz = q.size();  // 当前层节点数量for (int i = 0; i < sz; ++i) {Node* cur = q.front();q.pop();// 访问当前节点，附带深度信息std::cout << "depth = " << depth << ", val = " << cur->val << std::endl;// 所有子节点入队for (Node* child : cur->children) {q.push(child);}}depth++;  // 当前层遍历完毕，深度+1}
}

写法三：状态类记录深度（适配复杂权重场景）

作用：当节点间的“边权重”非1时（如深度递增非固定值），通过状态类可灵活记录节点深度，适用性更强。

// 状态类：记录节点及对应深度
class State {
public:Node* node;int depth;State(Node* n, int d) : node(n), depth(d) {}
};void levelOrderTraverse(Node* root) {if (root == nullptr) {return;}std::queue<State> q;q.push(State(root, 1));  // 根节点深度为1while (!q.empty()) {State state = q.front();q.pop();Node* cur = state.node;int depth = state.depth;// 访问当前节点，附带深度信息std::cout << "depth = " << depth << ", val = " << cur->val << std::endl;// 所有子节点入队，深度+1（若权重非1可调整增量）for (Node* child : cur->children) {q.push(State(child, depth + 1));}}
}

正题：动态规划（Dynamic Programming）核心框架

概要：动态规划的本质与核心问题

动态规划（DP）是求最值的优化算法，核心逻辑可总结为：

本质：穷举所有可能解，从中筛选最值；
核心三要素：
- 重叠子问题：存在重复计算的子问题，导致暴力解法效率低下；
- 最优子结构：原问题的最值可通过子问题的最值推导得出；
- 状态转移方程：描述原问题与子问题的关系，是穷举的数学表达（核心难点）；
解题步骤：明确「状态」→ 定义「选择」→ 推导「状态转移方程」→ 用备忘录/DP table优化重叠子问题。

动态规划三要素详解与案例：斐波那契数列

斐波那契数列虽非严格DP问题（无最值），但清晰展示了重叠子问题及优化过程，是理解DP的基础。

1. 暴力递归：暴露重叠子问题

斐波那契数列的数学定义为：
$\begin{cases} 0 & n=0 \\ 1 & n=1 \\ f(n-1) + f(n-2) & n>1 \end{cases}$

暴力递归实现：

// 计算第n个斐波那契数
int fib(int n) {// base case：最小子问题if (n == 0 || n == 1) {return n;}// 递归计算子问题return fib(n - 1) + fib(n - 2);
}

问题分析：

重叠子问题：递归树中存在大量重复计算。例如，计算f(5)时，f(3)被计算2次，f(2)被计算3次，且子树规模随n指数增长（如图1）。
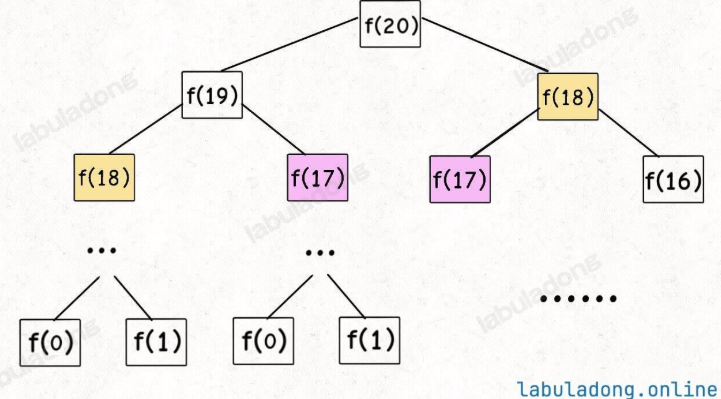
时间复杂度：子问题个数为递归树节点总数（约 $2^n$ ），每个子问题计算时间为 $O (1)$ ，总复杂度为 $O(2^n)$ （指数级，效率极低）。

2. 带备忘录的递归：消除重叠子问题

思路：用备忘录（数组/哈希表）记录已计算的子问题结果，避免重复计算。

实现代码：

int fib(int n) {if (n < 0) return -1;  // 非法输入处理// 备忘录：存储f(0)~f(n)的结果，初始化为-1（未计算）std::vector<int> memo(n + 1, -1);// 带备忘录的递归return dp(memo, n);
}// 辅助函数：用备忘录计算f(n)
int dp(std::vector<int>& memo, int n) {// base caseif (n == 0 || n == 1) {return n;}// 若已计算，直接返回备忘录结果（剪枝）if (memo[n] != -1) {return memo[n];}// 计算子问题并记录到备忘录memo[n] = dp(memo, n - 1) + dp(memo, n - 2);return memo[n];
}

优化效果：

递归树被剪枝为线性结构，每个子问题仅计算一次（如图2）。
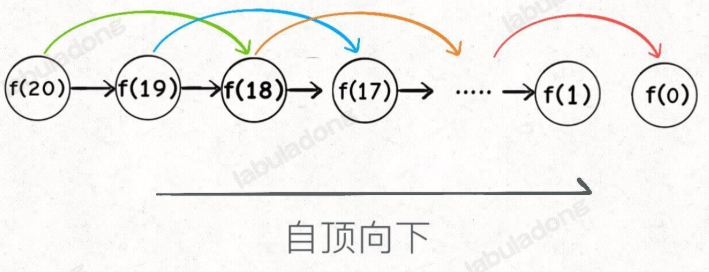
时间复杂度：子问题个数为 $O (n)$ ，总复杂度优化为 $O (n)$ 。

3. 自底向上的DP table：迭代实现

思路：从最小子问题（base case）出发，通过迭代计算更大的子问题，直至得到原问题结果（自底向上）。

实现代码：

int fib(int n) {// base caseif (n == 0 || n == 1) {return n;}// DP table：存储子问题结果std::vector<int> dp(n + 1);// 初始化base casedp[0] = 0;dp[1] = 1;// 从子问题逐步推导原问题for (int i = 2; i <= n; ++i) {dp[i] = dp[i - 1] + dp[i - 2];  // 状态转移方程}return dp[n];
}

核心逻辑：

DP table：dp[i]表示第i个斐波那契数，对应状态转移方程 $f (i) = f (i - 1) + f (i - 2)$ 。
自底向上：从i=2开始，利用已计算的dp[i-1]和dp[i-2]推导dp[i]，直至i=n。

4. 空间复杂度优化：滚动数组

观察：状态转移方程中，dp[i]仅依赖dp[i-1]和dp[i-2]，无需存储完整DP table。

优化实现：

int fib(int n) {// base caseif (n == 0 || n == 1) {return n;}// 用变量记录前两个状态int dp_i_1 = 1;  // 对应dp[i-1]，初始为f(1)=1int dp_i_2 = 0;  // 对应dp[i-2]，初始为f(0)=0for (int i = 2; i <= n; ++i) {// 计算当前状态int dp_i = dp_i_1 + dp_i_2;// 滚动更新前两个状态dp_i_2 = dp_i_1;dp_i_1 = dp_i;}return dp_i_1;  // 最终dp_i_1即为f(n)
}

效果：空间复杂度从 $O (n)$ 降至 $O (1)$ ，时间复杂度仍为 $O (n)$ 。

核心结论：动态规划的解题纲领

状态转移方程是核心：所有优化均围绕方程展开，暴力解法直接对应方程，备忘录/DP table仅为优化工具。
优化步骤固定：暴力递归（暴露问题）→ 备忘录（自顶向下剪枝）→ DP table（自底向上迭代）→ 滚动数组（空间优化）。
本质不变：自顶向下（递归+备忘录）与自底向上（DP table）本质相同，均通过消除重叠子问题提升效率。

凑零钱问题：动态规划的典型应用

斐波那契数列仅展示了重叠子问题的优化，而凑零钱问题则完整体现动态规划的三要素（重叠子问题、最优子结构、状态转移方程），是理解DP的核心案例。

问题定义与分析

力扣第322题「零钱兑换」：
给你 k 种面值的硬币（面值为 c1, c2, ..., ck，每种数量无限）和总金额 amount，求凑出该金额最少需要的硬币数；若无法凑出，返回 -1。

示例：
输入 coins = [1,2,5], amount = 11，输出 3（最优解：5+5+1）。

为何是动态规划问题？—— 最优子结构的判断

动态规划问题需具备最优子结构：原问题的最值可通过子问题的最值推导，且子问题间互相独立（无相互制约）。

凑零钱问题的最优子结构：
若要凑出金额 amount 的最少硬币数为 dp(amount)，则对于每种硬币面值 coin，dp(amount) 可由 dp(amount - coin) + 1 推导（即先凑出 amount - coin，再加一枚面值 coin 的硬币）。
子问题 dp(amount - coin) 之间互不干扰（选择一枚硬币后，剩余金额的最优解独立于其他选择），因此符合最优子结构。

动态规划三要素拆解

1. 状态（State）

状态是原问题和子问题中会变化的量。本题中，唯一变化的量是「目标金额」，即从 amount 逐步减少到 0 的过程，因此状态 = 目标金额 n。

2. 选择（Choice）

选择是导致状态变化的行为。本题中，选择一枚硬币会减少目标金额，因此选择 = 所有硬币的面值 coins。

3. 状态转移方程

定义 dp(n) 为：「凑出目标金额 n 所需的最少硬币数」。根据状态和选择，推导方程：

$\begin{cases} 0 & \text{if } n=0 \text{（无需硬币）} \\ -1 & \text{if } n<0 \text{（金额为负，无解）} \\ \min\{ dp(n - coin) + 1 \mid coin \in coins \} & \text{if } n>0 \text{（选择一枚硬币后，取子问题最小值+1）} \end{cases}$

解法一：暴力递归（暴露问题）

暴力递归直接实现状态转移方程，但存在大量重叠子问题，效率极低。

核心逻辑

通过递归遍历所有可能的硬币选择，计算子问题 dp(n - coin) 并取最小值加1。

class Solution {
public:int coinChange(vector<int>& coins, int amount) {return dp(coins, amount); // 最终答案为dp(amount)}private:// dp定义：凑出目标金额n所需的最少硬币数；若无解，返回-1int dp(vector<int>& coins, int n) {// base caseif (n == 0) return 0;    // 金额为0，无需硬币if (n < 0) return -1;    // 金额为负，无解int res = INT_MAX;       // 初始化结果为无穷大（用于后续取最小值）for (int coin : coins) { // 遍历所有选择（硬币面值）int subProblem = dp(coins, n - coin); // 计算子问题：n - coin的最少硬币数if (subProblem == -1) continue;       // 子问题无解，跳过当前硬币res = min(res, subProblem + 1);       // 更新最小值（子问题结果+当前硬币）}// 若res仍为INT_MAX，说明所有子问题无解，返回-1；否则返回resreturn res == INT_MAX ? -1 : res;}
};

问题分析

重叠子问题：递归树中大量子问题重复计算。例如，凑 amount=11 时，dp(9)、dp(6) 等子问题会被多次计算（如图1）。
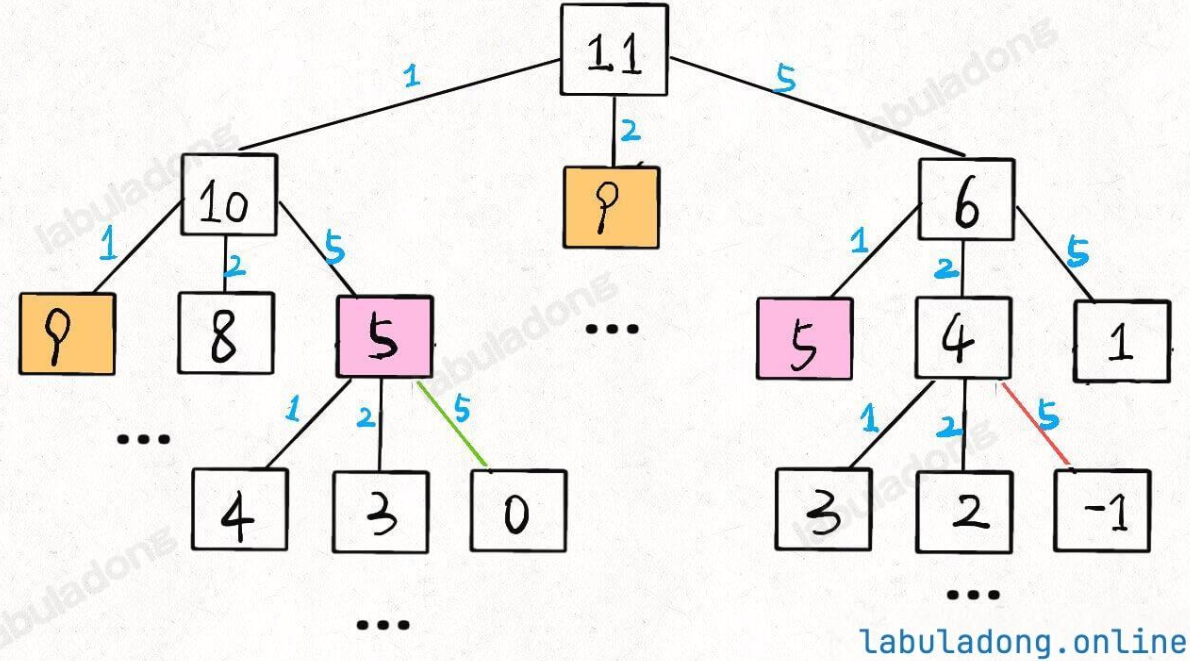
时间复杂度：最坏情况下为 $O(k^n)$ （ $k$ 为硬币种类， $n$ 为金额），指数级，无法通过大测试用例。

解法二：带备忘录的递归（优化重叠子问题）

通过备忘录记录已计算的子问题结果，消除重复计算，将时间复杂度降至多项式级别。

核心逻辑

用数组 memo 存储 dp(n) 的结果，每次计算前先查备忘录，避免重复递归。

class Solution {
private:vector<int> memo; // 备忘录：memo[n]记录dp(n)的结果public:int coinChange(vector<int>& coins, int amount) {memo.resize(amount + 1, -666); // 初始化备忘录为-666（标记未计算）return dp(coins, amount);}private:int dp(vector<int>& coins, int n) {// base caseif (n == 0) return 0;if (n < 0) return -1;// 查备忘录：若已计算，直接返回结果if (memo[n] != -666) return memo[n];int res = INT_MAX;for (int coin : coins) {int subProblem = dp(coins, n - coin);if (subProblem == -1) continue;res = min(res, subProblem + 1);}// 记录结果到备忘录memo[n] = (res == INT_MAX) ? -1 : res;return memo[n];}
};

优化效果

重叠子问题消除：每个子问题 dp(0)~dp(amount) 仅计算一次，子问题总数为 $O (n)$ 。
时间复杂度： $O (kn)$ （ $k$ 为硬币种类， $n$ 为金额），每个子问题需遍历 $k$ 种硬币。

解法三：DP数组迭代解法（自底向上）

将递归改为迭代，用DP数组存储子问题结果，进一步优化效率（避免递归栈开销）。

核心逻辑

定义 dp[i] 为凑出金额 i 所需的最少硬币数，从 i=0 开始自底向上计算，直至 i=amount。

class Solution {
public:int coinChange(vector<int>& coins, int amount) {// 初始化DP数组：dp[i]表示凑出金额i的最少硬币数vector<int> dp(amount + 1, amount + 1); // 初始化为amount+1（等效于无穷大，避免溢出）dp[0] = 0; // base case：金额0需0枚硬币// 遍历所有状态（金额从1到amount）for (int i = 0; i < dp.size(); ++i) {// 遍历所有选择（硬币面值）for (int coin : coins) {if (i - coin < 0) continue; // 子问题i-coin无解，跳过// 更新dp[i]：取当前值与子问题dp[i-coin]+1的最小值dp[i] = min(dp[i], 1 + dp[i - coin]);}}// 若dp[amount]仍为amount+1，说明无解，返回-1；否则返回dp[amount]return (dp[amount] == amount + 1) ? -1 : dp[amount];}
};

关键优化

初始值选择：用 amount + 1 代替 INT_MAX，避免 dp[i - coin] + 1 时的整型溢出（因最大硬币数不超过 amount，amount + 1 等效于无穷大）。
自底向上优势：无需递归栈，空间复杂度为 $O (n)$ （DP数组大小），时间复杂度仍为 $O (kn)$ 。

三种解法对比

解法	核心思路	时间复杂度	空间复杂度	适用场景
暴力递归	直接递归实现状态转移方程	$O(k^n)$	$O (n)$	理解问题本质，小规模输入
带备忘录递归	递归+备忘录剪枝	$O (kn)$	$O (n)$	中等规模输入，代码简洁
DP数组迭代	自底向上填充DP数组	$O (kn)$	$O (n)$	大规模输入，效率更高

三、动态规划总结

动态规划的核心是聪明地穷举：通过定义状态、选择和状态转移方程明确穷举逻辑，再用备忘录或DP数组消除重叠子问题，利用最优子结构推导结果。

解题流程

判断问题类型：是否存在最值问题，且具备最优子结构（子问题独立，原问题最值可由子问题最值推导）。
定义三要素：
- 状态：变化的量（如凑零钱问题中的目标金额）；
- 选择：导致状态变化的行为（如硬币面值）；
- 状态转移方程：描述原问题与子问题的关系（核心难点）。
实现与优化：
- 先写暴力递归（直接实现状态转移方程）；
- 用备忘录（自顶向下）或DP数组（自底向上）优化重叠子问题；
- 必要时压缩空间（如斐波那契的滚动数组）。