SingLoRA:单矩阵架构减半参数量,让大模型微调更稳定高效
随着深度学习模型规模的不断扩大,模型微调在保持性能的同时面临着计算成本和内存消耗的双重挑战。低秩适应(LoRA)技术通过引入低秩矩阵分解有效缓解了这一问题,但在实际应用中仍存在训练稳定性和参数效率方面的局限性。
SingLoRA作为一种创新的低秩适应方法,通过摒弃传统的双矩阵架构,采用单矩阵对称更新策略,在简化模型结构的同时显著提升了训练稳定性和参数效率。
🔍 SingLoRA技术原理
传统的LoRA方法通过在冻结的预训练权重中注入低秩矩阵乘积来实现权重更新:
W = W₀ + BA
其中B和A为可训练的低秩矩阵。这种双矩阵设计虽然减少了参数量,但矩阵间的尺度不匹配问题往往导致训练过程不稳定,需要精细的超参数调整。
SingLoRA通过引入对称矩阵更新机制,仅使用单一矩阵A进行权重更新:
W = W₀ + AAᵀ
这种对称更新策略从根本上消除了矩阵间尺度不匹配的问题,为训练过程提供了天然的稳定性保障。
技术优势分析
SingLoRA相比传统LoRA方法具有以下显著优势:
在参数效率方面,SingLoRA仅需要单一矩阵A,而传统LoRA需要同时维护矩阵B和A,这直接减少了一半的可训练参数。在训练稳定性方面,传统LoRA的权重更新形式
W = W₀ + BA
容易受到矩阵A和B之间尺度不匹配的影响,导致训练不稳定,而SingLoRA的对称更新
W = W₀ + AAᵀ
天然具有良好的数值稳定性。在超参数调整方面,传统LoRA通常需要为矩阵A和B设置不同的学习率以获得最佳性能,而SingLoRA仅需要单一学习率即可实现稳定训练。
技术特性对比如下:
方法 | 更新形式 | 可训练参数 | 稳定性 | 学习率调整 -----------|------------------|------------------|------------------|----------------------- LoRA | W = W₀ + BA | 高(2个矩阵) | 经常不稳定 | 需要(调整A和B) SingLoRA | W = W₀ + AAᵀ | 低(1个矩阵) | 设计上稳定 | 不需要(单一LR即可)
⚙️ 理论基础与收敛性分析
SingLoRA的优势不仅体现在实践中,更有着坚实的理论基础。通过对无限宽度神经网络动力学的深入分析,研究人员发现了传统LoRA方法在大规模模型中存在的根本性问题。
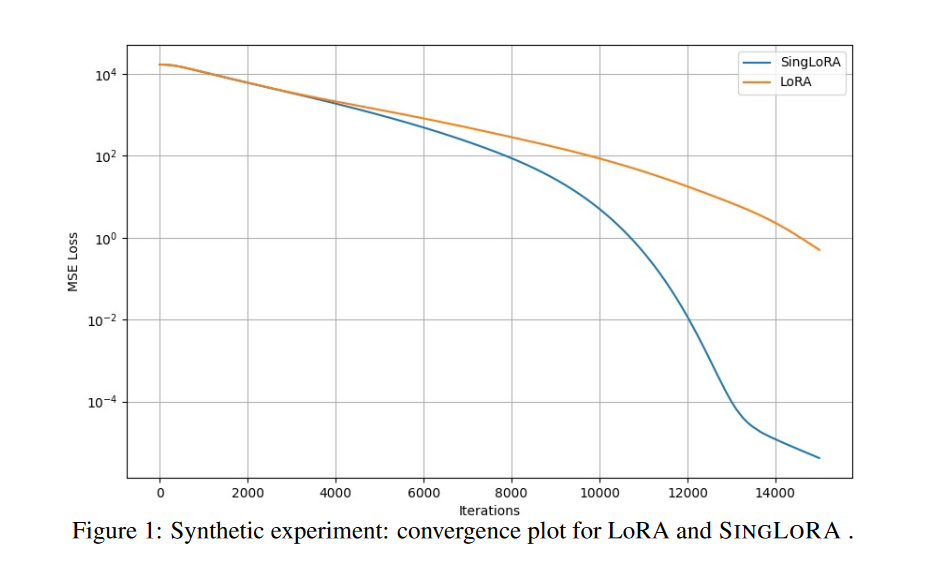
在无限宽度极限下,传统LoRA的双矩阵更新会随着网络宽度的增加而出现尺度发散现象,这种发散直接影响了梯度的稳定性和收敛性。相比之下,SingLoRA的对称更新机制能够保持梯度尺度的一致性,即使在大规模模型中也能确保训练过程的稳定性。
这一理论优势使得SingLoRA能够与标准优化器(如Adam或SGD)无缝集成,无需额外的数值稳定化技巧或复杂的学习率调度策略。
📊 实验验证与性能评估
自然语言处理任务评估
在GLUE基准测试中,我们使用RoBERTa和GPT-2模型在MNLI、QQP和QNLI任务上进行了全面评估:
模型 | 方法 | 准确率 (%) | 参数量 (百万)
----------|-----------|---------------|-------------------
RoBERTa | LoRA | 88.3 | 0.15 | LoRA+ | 89.2 | 0.15 | DoRA | 89.2 | 0.16 | SingLoRA | 89.2 | 0.075GPT-2 | LoRA | 84.6 | 1.78 | LoRA+ | 85.6 | 1.78 | DoRA | 85.7 | 1.78 | SingLoRA | 85.7 | 0.89
实验结果表明,SingLoRA在使用更少参数的情况下仍能达到或超越现有方法的性能水平。
大语言模型微调实验
在LLaMA-7B模型的MNLI任务评估中,SingLoRA展现出了更为突出的优势:
方法 | 准确率 (%) | 参数量 (百万) -----------|---------------|------------------- LoRA | 89.1 | 20 LoRA+ | 90.2 | 20 DoRA | 90.6 | 21 SingLoRA | 91.3 | 12
SingLoRA不仅在准确率方面取得了最优结果,同时参数效率提升了40%,这一显著优势在大规模模型部署中具有重要的实际意义。
计算机视觉任务验证
为了验证SingLoRA在多模态任务中的有效性,在个性化图像生成任务DreamBooth上进行了评估。使用Stable Diffusion模型的实验结果如下:
方法 | CLIP Img | CLIP Txt | DINO Sim | Rank | 参数量 -----------|----------|----------|-----------|------|-------- LoRA | 0.677 | 0.319 | 0.143 | 8 | 0.9M LoRA+ | 0.688 | 0.315 | 0.150 | 8 | 0.9M DoRA | 0.687 | 0.317 | 0.148 | 8 | 0.9M SingLoRA | 0.690 | 0.317 | 0.151 | 16 | 0.9M
在相同的参数预算限制下,SingLoRA在图像保真度指标上实现了最优性能,证明了其在视觉任务中的有效性。
训练稳定性与超参数敏感性分析
SingLoRA的一个重要技术优势是其对学习率变化的适应性。在LLaMA-7B模型的敏感性分析实验中,论文观察到了显著的稳定性改善:传统LoRA方法的性能随学习率变化的波动幅度高达4.8%,而SingLoRA的性能波动控制在1%以内。
这种稳定性使得SingLoRA在实际部署中更加可靠,特别是在计算资源受限或需要快速部署的场景中,用户无需进行复杂的超参数调整即可获得稳定的性能表现。
总结
SingLoRA作为参数高效微调领域的一项重要技术创新,通过单矩阵对称更新机制实现了显著的技术改进。该方法具有以下核心优势:参数效率显著提升,单一矩阵设计减少了参数量和实现复杂度;训练稳定性从设计层面得到保障,无需额外的数值稳定化处理;广泛的模型适用性,在文本和图像模型上均表现出色;良好的扩展性,可与DoRA或LoRA+等其他优化技术结合使用。
SingLoRA的理论基础扎实,实验验证全面,为大规模模型的高效微调提供了新的技术路径,在实际应用中具有重要的推广价值。
论文链接:
https://avoid.overfit.cn/post/9634e946125f43e482bd254e659bb37b
