学习笔记(37):构建一个房价预测模型，并通过可视化全面评估模型效果

学习笔记(37):构建一个房价预测模型，并通过可视化全面评估模型效果

一、模型目标

1. 核心目标

用线性回归算法，基于房屋特征（面积、房龄、卧室数量等）预测房价，并通过多种可视化方式直观展示模型的预测效果和特征重要性。

2. 关键步骤

• 数据准备：支持加载真实数据或生成模拟数据（包含房价、面积、房龄等特征）。
• 模型训练：使用线性回归算法，通过特征学习房价的预测规则。
• 效果评估：
  • 预测值 vs 真实值：散点图展示模型预测的准确性。
  • 残差分析：直方图展示预测误差的分布，评估模型偏差。
  • 特征重要性：条形图展示哪些因素对房价影响最大（如面积、停车位）。
  • 置信区间：展示预测的不确定性（误差范围）。

3. 对用户的价值

• 快速理解模型表现：通过图表直观判断模型是否靠谱。
• 挖掘房价影响因素：发现哪些特征对房价影响最大（如 “有停车位” 可能比 “房龄” 更重要）。
• 识别改进方向：如果模型误差大，可以针对性调整特征或更换算法。

4. 一句话总结

这是一个房价预测模型的 “体检报告生成器”，它能：

• 训练模型预测房价
• 用图表展示预测效果
• 告诉你哪些因素决定了房价高低

适合用于房地产数据分析、房价预测研究，或作为机器学习入门的实践案例。

二、房价预测模型代码解析

1. 导入必要的库

import pandas as pd              # 用于数据处理和分析
import matplotlib.pyplot as plt  # 绘图工具
import seaborn as sns            # 基于matplotlib的高级绘图工具
import numpy as np               # 用于科学计算
import os                        # 用于文件和目录操作
from sklearn.linear_model import LinearRegression  # 线性回归模型
from sklearn.model_selection import train_test_split  # 数据分割工具
from sklearn.metrics import mean_squared_error, r2_score  # 模型评估指标

作用：引入后续代码需要的所有工具包，就像厨师准备好锅碗瓢盆一样。

2. 设置中文显示

plt.rcParams["font.family"] = ["SimHei", "Microsoft YaHei"]  # 指定中文字体
plt.rcParams['axes.unicode_minus'] = False  # 解决负号显示问题

作用：确保图表中的中文能正常显示（否则可能显示为方块），并修复负号显示异常。

3. 数据加载函数 load_data()

def load_data(file_path=None):"""加载或生成房价数据"""if file_path and os.path.exists(file_path):data = pd.read_csv(file_path)  # 读取指定路径的CSV文件print(f"已加载数据：{data.shape[0]}条记录，{data.shape[1]}个特征")else:print("未找到数据，生成模拟数据...")np.random.seed(42)  # 设置随机种子，确保结果可复现size = 500  # 生成500条样本数据# 用随机数生成各特征（房价、面积、房龄等）data = pd.DataFrame({'price': np.random.normal(15000, 3000, size),  # 房价（万元），正态分布'area': np.random.normal(100, 20, size),       # 面积（平方米）'age': np.random.randint(1, 30, size),         # 房龄（年）'bedrooms': np.random.randint(1, 6, size),     # 卧室数'bathrooms': np.random.randint(1, 4, size),    # 浴室数'parking': np.random.randint(0, 2, size),      # 是否有停车位（0/1）'floor': np.random.randint(1, 30, size)        # 楼层})# 增强房价与特征的关系（让房价更依赖面积和房龄）data['price'] = data['price'] + 50 * data['area'] - 100 * data['age']data['price'] = data['price'].clip(lower=5000)  # 设置房价下限，避免负值return data

作用：

• 如果指定路径有 CSV 文件，就加载真实数据；
• 否则，生成模拟数据（符合正态分布和基本逻辑，如面积越大房价越高）。
  核心逻辑：模拟数据时，用数学公式 price = 基础值 + 50×面积 - 100×房龄 确保特征与房价有合理关系。

4. 主函数 plot_model_results()

def plot_model_results(data, price_col='price', features=None):"""训练线性回归模型并可视化结果"""if features is None:features = ['area', 'age', 'bedrooms', 'bathrooms', 'parking', 'floor']# 准备数据X = data[features]  # 特征矩阵（自变量）y = data[price_col]  # 目标变量（因变量：房价）# 划分训练集和测试集（80%训练，20%测试）X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)# 训练模型model = LinearRegression()  # 创建线性回归模型model.fit(X_train, y_train)  # 用训练数据拟合模型y_pred = model.predict(X_test)  # 用测试数据进行预测

关键步骤：

1. 数据准备：提取特征（如面积、房龄）和目标变量（房价）。
2. 数据分割：将数据分为训练集（模型学习用）和测试集（模型验证用）。
3. 模型训练与预测：用训练数据教会模型 “特征与房价的关系”，再用测试数据验证模型效果。

5. 创建保存图表的文件夹

    if not os.path.exists('model_plots'):
os.makedirs('model_plots')  # 如果文件夹不存在，就创建它

作用：确保后续生成的图表有地方存放。

6. 预测值 vs 真实值散点图

    plt.figure(figsize=(10, 6))  # 创建一个10×6英寸的图表plt.scatter(y_test, y_pred, alpha=0.6, color='skyblue')  # 绘制散点图plt.plot([y.min(), y.max()], [y.min(), y.max()], 'r--', lw=2)  # 绘制理想线（预测=真实）plt.xlabel('真实房价 (万元)')plt.ylabel('预测房价 (万元)')plt.title('房价预测模型：预测值 vs 真实值')plt.grid(alpha=0.3)  # 添加网格线，透明度30%plt.tight_layout()  # 自动调整布局，避免元素重叠plt.savefig('model_plots/prediction_vs_true.png', dpi=300)  # 保存高清图片plt.show()  # 显示图表

核心逻辑：

• 散点图：每个点代表一套房子，横坐标是真实房价，纵坐标是预测房价。
• 红色虚线：理想情况下，所有点应该落在这条线上（预测完全准确）。
• 分析重点：点越靠近红线，模型越准。

7. 残差分布图

    residuals = y_test - y_pred  # 计算残差（真实值 - 预测值）plt.figure(figsize=(10, 6))sns.histplot(residuals, kde=True, color='orange')  # 绘制直方图和核密度估计曲线plt.axvline(residuals.mean(), color='blue', linestyle='dashed', label=f'平均误差: {residuals.mean():.2f} 万元')  # 添加平均误差线plt.xlabel('预测残差 (万元)')plt.ylabel('频数')plt.title('房价预测模型：残差分布')plt.legend()  # 显示图例plt.grid(alpha=0.3)plt.tight_layout()plt.savefig('model_plots/residuals_distribution.png', dpi=300)plt.show()

核心逻辑：

• 残差：衡量模型预测的误差（残差 = 0 表示预测完美）。
• 直方图：展示残差的分布情况，理想情况是围绕 0 对称分布。
• 平均误差线：直观看到模型整体的偏差方向（正或负）。

8. 特征重要性图

    # 将模型系数转为Series，按重要性排序importance = pd.Series(model.coef_, index=features).sort_values()plt.figure(figsize=(10, 6))importance.plot(kind='barh', color='lightgreen')  # 绘制水平条形图plt.xlabel('特征系数')plt.ylabel('特征名称')plt.title('房价预测模型：特征重要性')plt.grid(axis='x', alpha=0.3)  # 只显示水平网格线plt.tight_layout()plt.savefig('model_plots/feature_importance.png', dpi=300)plt.show()

核心逻辑：

• 线性回归系数：系数越大，表示该特征对房价的影响越大（正系数表示正相关，负系数表示负相关）。
• 条形图：直观展示各特征的重要性排序。
• 洞察：例如，parking 系数为正且大 → 有停车位会显著提高房价。

9. 预测置信区间图

    plt.figure(figsize=(12, 6))# 绘制带误差线的真实值（前50个样本）plt.errorbar(range(50), y_test[:50], yerr=abs(residuals[:50]), fmt='o', color='blue', ecolor='lightblue', alpha=0.7, label='真实值±误差')# 绘制预测值（红色方块）plt.plot(range(50), y_pred[:50], 'rs', alpha=0.5, label='预测值')plt.xlabel('样本编号')plt.ylabel('房价 (万元)')plt.title('房价预测模型：预测置信区间（前50个样本）')plt.legend()plt.grid(alpha=0.3)plt.tight_layout()plt.savefig('model_plots/prediction_confidence.png', dpi=300)plt.show()

核心逻辑：

• 误差线（蓝色竖线）：表示真实房价可能的波动范围（基于残差大小）。
• 红色方块：模型的预测值。
• 分析重点：误差线越短，模型对该样本的预测越有把握。

10. 打印模型性能指标

    print("\n=== 模型性能指标 ===")print(f"均方误差 (MSE): {mean_squared_error(y_test, y_pred):.2f}")print(f"均方根误差 (RMSE): {np.sqrt(mean_squared_error(y_test, y_pred)):.2f}")print(f"决定系数 (R²): {r2_score(y_test, y_pred):.4f}")print("\n=== 特征重要性排序 ===")print(importance.sort_values(ascending=False))

关键指标解释：

• MSE/RMSE：误差平方的平均值（越小越好），RMSE 是 MSE 的平方根，与房价单位一致。
• R²：模型解释数据变异的比例（0~1，越接近 1 越好），表示 “特征能解释多少房价变化”。

11. 主程序入口

if __name__ == "__main__":# 文件路径（替换为你的CSV文件路径）file_path = 'house_prices.csv'# 加载数据data = load_data(file_path)# 训练模型并绘制结果图plot_model_results(data)

作用：

• 当直接运行这个脚本时，会依次执行数据加载、模型训练和结果可视化。
• 若作为模块被其他脚本导入，则不会执行。

总结

这段代码实现了一个完整的房价预测流程：

1. 数据准备：加载或生成房价数据。
2. 模型训练：用线性回归建立特征与房价的关系。
3. 结果可视化：通过 4 种图表（预测 vs 真实、残差分布、特征重要性、置信区间）直观评估模型效果。

核心目的是帮助你理解：

• 哪些因素对房价影响最大？
• 模型预测的准确性如何？
• 预测的不确定性有多大？

三、完整代码和执行结果

3.1.完整代码

import pandas as pd
import matplotlib.pyplot as plt
import seaborn as sns
import numpy as np
import os
from sklearn.linear_model import LinearRegression
from sklearn.model_selection import train_test_split
from sklearn.metrics import mean_squared_error, r2_score# 设置中文显示
plt.rcParams["font.family"] = ["SimHei", "Microsoft YaHei"]
plt.rcParams['axes.unicode_minus'] = Falsedef load_data(file_path=None):"""加载或生成房价数据"""if file_path and os.path.exists(file_path):data = pd.read_csv(file_path)print(f"已加载数据：{data.shape[0]}条记录，{data.shape[1]}个特征")else:print("未找到数据，生成模拟数据...")np.random.seed(42)size = 500data = pd.DataFrame({'price': np.random.normal(15000, 3000, size),  # 房价（万元）'area': np.random.normal(100, 20, size),  # 面积（平方米）'age': np.random.randint(1, 30, size),  # 房龄（年）'bedrooms': np.random.randint(1, 6, size),  # 卧室数'bathrooms': np.random.randint(1, 4, size),  # 浴室数'parking': np.random.randint(0, 2, size),  # 是否有停车位'floor': np.random.randint(1, 30, size)  # 楼层})# 增强房价与特征的关系data['price'] = data['price'] + 50 * data['area'] - 100 * data['age']data['price'] = data['price'].clip(lower=5000)  # 设置价格下限return datadef plot_model_results(data, price_col='price', features=None):"""训练线性回归模型并可视化结果"""if features is None:features = ['area', 'age', 'bedrooms', 'bathrooms', 'parking', 'floor']# 准备数据X = data[features]y = data[price_col]X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)# 训练模型model = LinearRegression()model.fit(X_train, y_train)y_pred = model.predict(X_test)# 创建保存图表的文件夹if not os.path.exists('model_plots'):os.makedirs('model_plots')# 1. 预测值 vs 真实值散点图plt.figure(figsize=(10, 6))plt.scatter(y_test, y_pred, alpha=0.6, color='skyblue')plt.plot([y.min(), y.max()], [y.min(), y.max()], 'r--', lw=2)  # 理想线plt.xlabel('真实房价 (万元)')plt.ylabel('预测房价 (万元)')plt.title('房价预测模型：预测值 vs 真实值')plt.grid(alpha=0.3)plt.tight_layout()plt.savefig('model_plots/prediction_vs_true.png', dpi=300)plt.show()# 2. 残差分布图residuals = y_test - y_predplt.figure(figsize=(10, 6))sns.histplot(residuals, kde=True, color='orange')plt.axvline(residuals.mean(), color='blue', linestyle='dashed',label=f'平均误差: {residuals.mean():.2f} 万元')plt.xlabel('预测残差 (万元)')plt.ylabel('频数')plt.title('房价预测模型：残差分布')plt.legend()plt.grid(alpha=0.3)plt.tight_layout()plt.savefig('model_plots/residuals_distribution.png', dpi=300)plt.show()# 3. 特征重要性图（线性回归系数）importance = pd.Series(model.coef_, index=features).sort_values()plt.figure(figsize=(10, 6))importance.plot(kind='barh', color='lightgreen')plt.xlabel('特征系数')plt.ylabel('特征名称')plt.title('房价预测模型：特征重要性')plt.grid(axis='x', alpha=0.3)plt.tight_layout()plt.savefig('model_plots/feature_importance.png', dpi=300)plt.show()# 4. 预测置信区间图（仅展示前50个样本）plt.figure(figsize=(12, 6))plt.errorbar(range(50), y_test[:50], yerr=abs(residuals[:50]), fmt='o',color='blue', ecolor='lightblue', alpha=0.7, label='真实值±误差')plt.plot(range(50), y_pred[:50], 'rs', alpha=0.5, label='预测值')plt.xlabel('样本编号')plt.ylabel('房价 (万元)')plt.title('房价预测模型：预测置信区间（前50个样本）')plt.legend()plt.grid(alpha=0.3)plt.tight_layout()plt.savefig('model_plots/prediction_confidence.png', dpi=300)plt.show()# 打印模型性能指标print("\n=== 模型性能指标 ===")print(f"均方误差 (MSE): {mean_squared_error(y_test, y_pred):.2f}")print(f"均方根误差 (RMSE): {np.sqrt(mean_squared_error(y_test, y_pred)):.2f}")print(f"决定系数 (R²): {r2_score(y_test, y_pred):.4f}")print("\n=== 特征重要性排序 ===")print(importance.sort_values(ascending=False))if __name__ == "__main__":# 文件路径（替换为你的CSV文件路径）file_path = 'house_prices.csv'# 加载数据data = load_data(file_path)# 训练模型并绘制结果图plot_model_results(data)

3.2.执行结果

3.2.1、房价预测模型的核心评估图

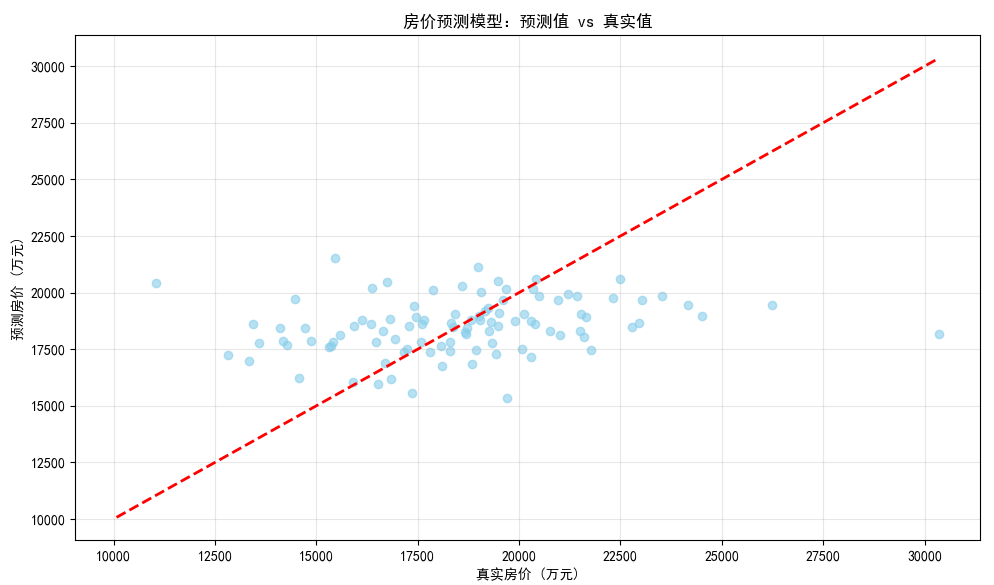
房价预测模型的核心评估图，专门用来直观判断模型预测准不准。下面用最白话的方式拆解，让你秒懂每个细节：

1. 先看标题：「预测值 vs 真实值」

这张图的任务是回答一个关键问题：模型预测的房价，和真实房价到底有多像？

2. 坐标轴是啥意思？

• 横坐标（X 轴）：真实房价（万元）
  → 房子实际卖了多少钱（比如 20000 万元）

• 纵坐标（Y 轴）：预测房价（万元）
  → 模型猜这套房子值多少钱（比如 19000 万元）

3. 图里的元素代表啥？

• 蓝色圆点：每一套房子的「真实值 vs 预测值」
  → 比如某个圆点在 X=20000，Y=19000 → 真实房价 20000 万，模型预测 19000 万

• 红色虚线：「预测完美线」（理想状态）
  → 如果模型 100% 准确，所有蓝色圆点应该全部落在这条线上（因为此时预测值 = 真实值）

4. 怎么看模型准不准？

• 理想情况：蓝色圆点紧紧贴着红色虚线 → 模型超准，预测值≈真实值

• 实际情况：

  • 如果圆点大部分靠近虚线 → 模型还不错，误差小
  • 如果圆点离虚线越远 → 模型越不准，误差大

5. 举个具体例子

比如有个圆点：

• X=20000（真实房价 20000 万）
• Y=18000（模型预测 18000 万）
  → 离红色虚线远 → 模型这次预测偏差大（少猜了 2000 万）

6. 这张图的核心结论

从图中能直接看出：

• 模型整体有一定预测能力（大部分圆点集中在虚线附近）
• 但存在误差（部分圆点偏离虚线）
• 误差方向：有些预测值高于真实值，有些低于（分布相对对称，说明模型没有系统性偏差）

7. 对后续分析的价值

• 如果圆点太分散 → 模型需要优化（换算法、加特征）
• 如果圆点集中但偏离虚线 → 模型有系统性偏差（比如总是预测偏低）
• 如果圆点紧贴虚线 → 模型超神（现实中很少见，说明数据或模型有特殊情况）

总结一下：
这张图是模型的 “期中考试成绩单”，蓝色圆点越靠近红色虚线，模型成绩越好。通过它，你能一眼判断模型预测房价的靠谱程度～

3.2.2、房价预测模型的「残差分布图」

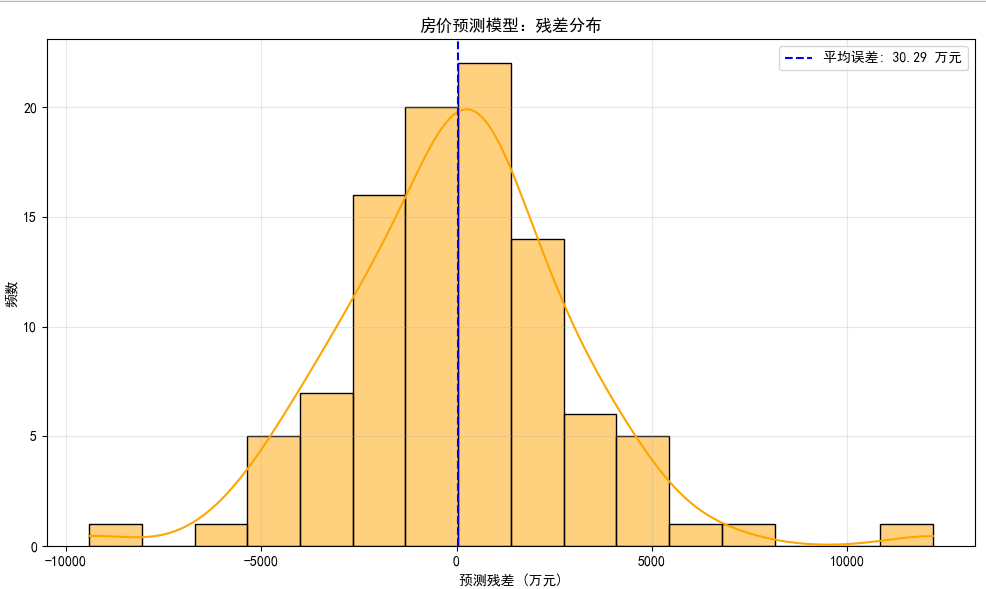
房价预测模型的「残差分布图」，专门用来分析模型预测误差的规律。给你拆解成小白也能懂的版本：

1. 先搞懂「残差」是啥？

残差 = 真实房价 - 模型预测房价

• 如果残差 = 0 → 模型预测完美（几乎不可能）
• 如果残差 > 0 → 模型预测低于真实房价（比如真实值 200 万，模型猜 190 万，残差 +10 万）
• 如果残差 < 0 → 模型预测高于真实房价（比如真实值 200 万，模型猜 210 万，残差 -10 万）

2. 图里每个部分啥意思？

• 横坐标（X 轴）：残差的大小（万元）
  比如 -10000 代表 “模型预测比真实房价高 1 万元”，+5000 代表 “模型预测比真实房价低 0.5 万元”

• 纵坐标（Y 轴）：「残差出现的次数」（专业词叫 “频数”）
  比如某个柱子高度是 20 → 代表有 20 套房的残差落在这个区间里

3. 核心怎么看？

（1）看整体分布形状

• 理想情况：残差集中在 0 附近，左右对称（像 “山峰” 一样）
  → 说明模型误差小，且 “预测高了” 和 “预测低了” 的情况差不多

• 你的图里：残差基本围绕 0 分布，说明模型整体误差不大；但左右不算特别对称（左边柱子稍矮、右边稍高），可能偶尔会有 “预测偏低” 的情况

（2）看「平均误差」（右上角蓝色虚线）

• 图里平均误差 = 30.29 万元
  → 代表所有房子的残差平均下来，模型预测和真实房价差 30 万左右（这个值越小，模型越准）

（3）看极端值

• 左右两端的小柱子（比如残差 -10000、+10000 附近）
  → 代表模型偶尔会出现超大误差（比如某套房真实 200 万，模型猜成 190 万或 210 万）

4. 总结这张图想告诉你啥？

• 模型整体误差不大，大部分预测的残差集中在 0 附近
• 平均误差 30 万左右（具体好不好，得看房价本身的量级，比如房价是几百万的话，这个误差算能接受）
• 偶尔会有 “预测偏高 / 偏低” 特别多的情况，可能需要排查这些极端案例，看看是不是数据异常

如果是新手，记住核心结论：残差越集中在 0，模型越稳；平均误差越小，模型越准～

3.2.3、“特征重要性” 柱状图

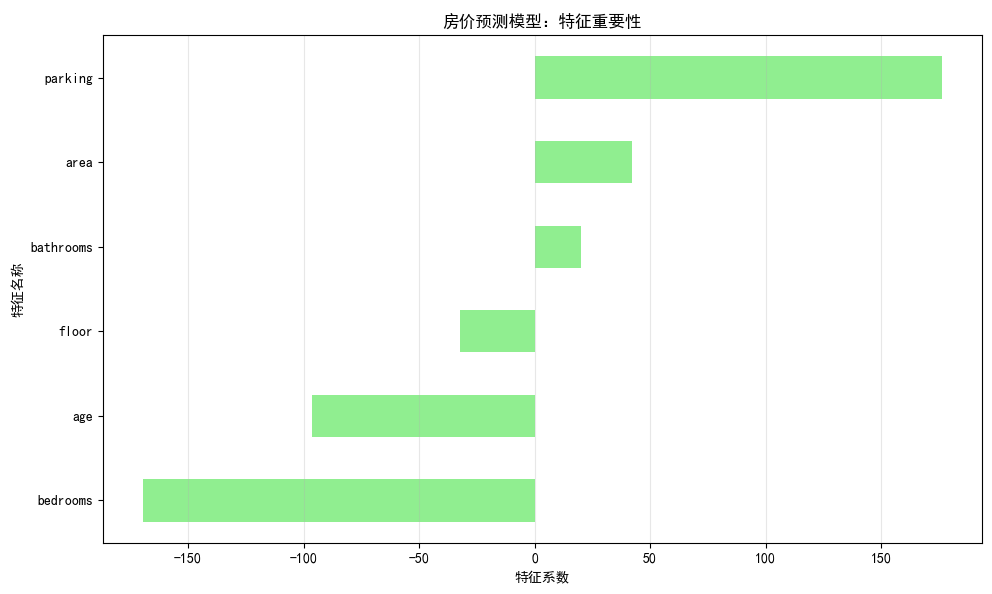
房价预测模型的 “特征重要性” 柱状图，用来展示不同因素（比如面积、房龄）对房价影响的大小和方向，小白版解读来啦：

1. 先搞懂「特征系数」是啥？

模型（比如线性回归）会给每个特征算一个系数，代表：这个特征每变化 1 单位，房价会怎么变

• 系数为正 → 特征越大，房价越高（比如 area 面积越大，房价越高）
• 系数为负 → 特征越大，房价越低（比如 age 房龄越大，房价越低）

2. 图里每个部分啥意思？

• 纵坐标（Y 轴）：特征名称
  比如 parking（是否有停车位）、area（面积）、age（房龄）等

• 横坐标（X 轴）：特征系数的大小
  正数代表 “特征越大，房价越高”；负数代表 “特征越大，房价越低”

3. 怎么看每个特征的影响？

（1）parking（是否有停车位）

• 系数是很大的正数 → 有停车位的房子，房价会显著更高（模型认为停车位对房价拉升作用最大）

（2）area（面积）

• 系数是正数 → 面积越大，房价越高（符合常识）

（3）age（房龄）

• 系数是负数 → 房龄越大，房价越低（房龄老的房子更便宜）

（4）bedrooms（卧室数量）

• 系数是很大的负数 → 这里要注意！可能是模型计算的 “反向关系”（比如卧室越多，房价反而越低？这可能和数据有关，比如小房子硬改多卧室，实际面积小，反而拉低房价）

4. 核心结论怎么读？

• 影响方向：看系数正负，知道 “特征越大，房价是涨还是跌”
• 影响大小：看柱子长度，柱子越长，对房价影响越大（不管正负）

比如：

• parking 对房价的正向影响最大（有车位房价涨得最多）
• bedrooms 对房价的负向影响最大（卧室多反而拉低房价，可能数据里有特殊情况）

5. 注意 “异常” 情况

像 bedrooms 系数是负的且绝对值大，可能是数据问题（比如小房子强行隔多卧室，实际面积小、居住体验差），也可能是模型没调好。这种 “反常识” 的结果，反而值得注意，排查下数据或模型是否有问题～

总结一下：

• 柱子越长 → 特征对房价影响越大
• 正数 → 特征越大，房价越高；负数 → 特征越大，房价越低
  通过这张图，能快速看出 “哪些因素对房价影响最大”，以及 “影响是好是坏”～

3.2.4、预测置信区间图

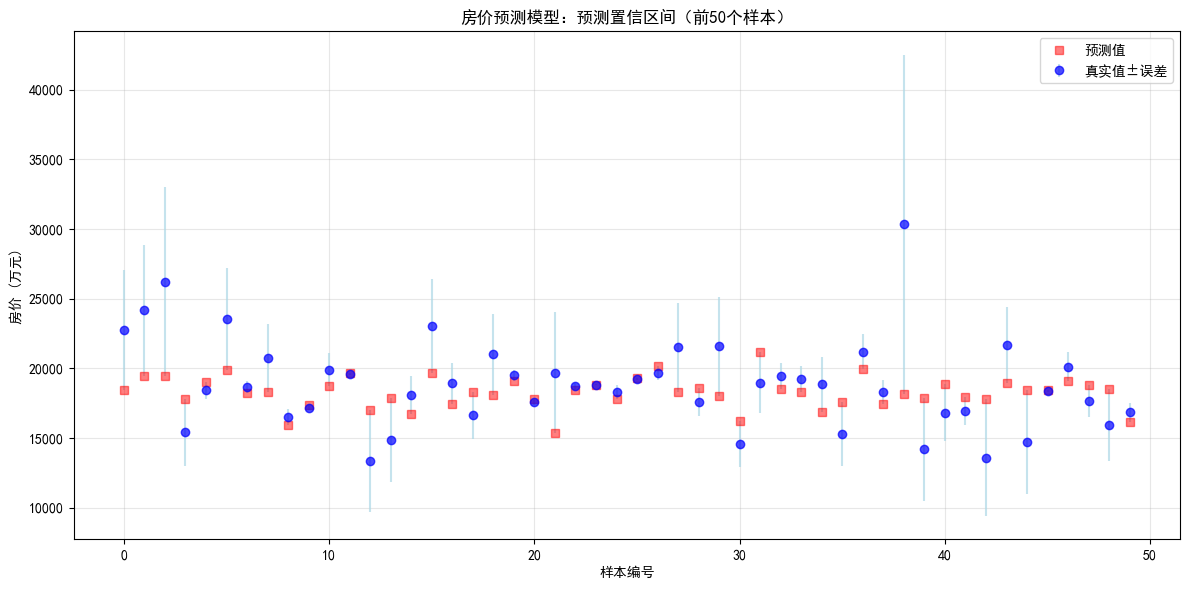
房价预测模型的预测置信区间图，专门用来展示模型预测的 “不确定性” ，也就是模型对前 50 套房子预测时，真实房价可能的波动范围。以下用超白话拆解，保证小白能懂：

1. 先理解「置信区间」是啥？

模型预测房价时，不是只给一个确定值，还会说：“我猜这套房值 200 万，但真实价格可能在 190 - 210 万之间”
→ 这里的 190 - 210 万 就是置信区间，代表 “真实值有很大概率落在这个区间里”

2. 图里每个元素啥意思？

• 横坐标（X 轴）：样本编号（前 50 套房子，从 0 到 50 号）
• 纵坐标（Y 轴）：房价（万元）
• 蓝色圆点：房子的真实房价（实际成交价）
• 蓝色竖线：真实房价的置信区间（竖线越长，说明模型对这套房的预测越不确定，真实房价可能波动越大）
• 红色方块：模型的预测房价（模型觉得这套房值多少钱）

3. 怎么看这张图？

（1）看预测准不准

• 如果 红色方块（预测值） 靠近 蓝色圆点（真实值） → 模型预测准
• 如果红色方块离蓝色圆点远 → 模型预测偏了

（2）看置信区间稳不稳

• 蓝色竖线越短 → 模型对这套房的预测越 “确定”（真实房价大概率接近预测值）
• 蓝色竖线越长 → 模型越 “没把握”（真实房价可能偏离预测值很多）

4. 举个具体例子（看某一套房）

比如第 10 号样本：

• 蓝色圆点（真实房价）≈ 18000 万元
• 红色方块（预测房价）≈ 19000 万元 → 预测稍高，但不算离谱
• 蓝色竖线不长 → 模型对这套房的预测比较有把握，真实房价应该就在 17000 - 20000 之间

5. 核心结论

• 大部分红色方块和蓝色圆点比较接近 → 模型整体预测能力不错
• 蓝色竖线长度差不多 → 模型对前 50 套房的预测不确定性比较稳定
• 如果某套房竖线特别长、且红方块离蓝圆点远 → 要注意！可能是这套房有特殊情况（比如户型奇葩、地段特殊），模型没见过，预测不准

简单说，这张图能让你看到：模型对每套房子的预测值准不准，以及模型自己对预测结果有多大 “把握” 。竖线越短、红方块越靠近蓝圆点，模型越靠谱～