当前位置：首页 > news >正文

用 K-means 算法实现水果分堆

news 2025/7/16 6:10:47

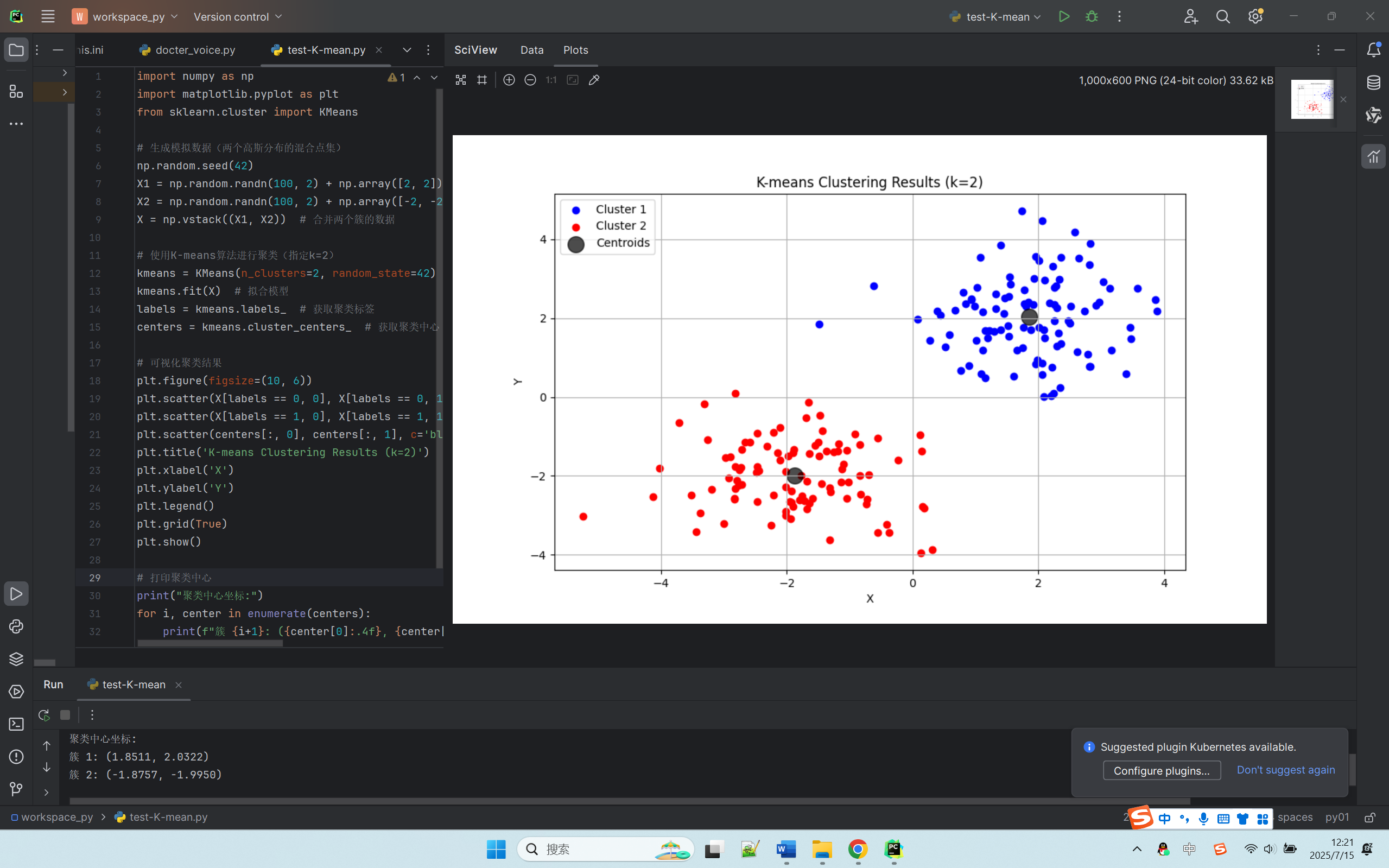
先看运行效果：

import numpy as np
import matplotlib.pyplot as plt
from sklearn.cluster import KMeans# 生成模拟数据（两个高斯分布的混合点集）
np.random.seed(42)
X1 = np.random.randn(100, 2) + np.array([2, 2])  # 第一簇数据，中心在(2,2)
X2 = np.random.randn(100, 2) + np.array([-2, -2])  # 第二簇数据，中心在(-2,-2)
X = np.vstack((X1, X2))  # 合并两个簇的数据# 使用K-means算法进行聚类（指定k=2）
kmeans = KMeans(n_clusters=2, random_state=42)
kmeans.fit(X)  # 拟合模型
labels = kmeans.labels_  # 获取聚类标签
centers = kmeans.cluster_centers_  # 获取聚类中心# 可视化聚类结果
plt.figure(figsize=(10, 6))
plt.scatter(X[labels == 0, 0], X[labels == 0, 1], c='blue', label='Cluster 1')
plt.scatter(X[labels == 1, 0], X[labels == 1, 1], c='red', label='Cluster 2')
plt.scatter(centers[:, 0], centers[:, 1], c='black', s=200, alpha=0.7, label='Centroids')
plt.title('K-means Clustering Results (k=2)')
plt.xlabel('X')
plt.ylabel('Y')
plt.legend()
plt.grid(True)
plt.show()# 打印聚类中心
print("聚类中心坐标:")
for i, center in enumerate(centers):print(f"簇 {i+1}: ({center[0]:.4f}, {center[1]:.4f})")

第一步：准备数据（模拟 “水果摊分堆”）

# 生成模拟数据（两个高斯分布的混合点集）

np.random.seed(42)

X1 = np.random.randn(100, 2) + np.array([2, 2]) # 第一堆水果：苹果（集中在货架右上角）

X2 = np.random.randn(100, 2) + np.array([-2, -2]) # 第二堆水果：橘子（集中在货架左下角）

X = np.vstack((X1, X2)) # 把两堆水果混在一起，放在同一个货架上

说明：

我们先 “假装” 有两堆水果（苹果和橘子），它们各自集中在货架的不同位置。np.random.randn() 就像是把水果随机撒在各自区域，但不会撒得太离谱（符合高斯分布）。最后把两堆水果混在一起，假装我们不知道哪些是苹果、哪些是橘子。

第二步：K-means 算法（让电脑帮忙 “分堆”）

# 使用K-means算法进行聚类（指定k=2）

kmeans = KMeans(n_clusters=2, random_state=42)

kmeans.fit(X) # 让电脑“观察”这些水果，尝试分成两堆

labels = kmeans.labels_ # 获取每一个水果的“分类标签”（0或1）

centers = kmeans.cluster_centers_ # 获取两堆水果的“中心位置”（平均坐标）

说明：

我们告诉电脑：“这里有一堆水果，请帮我分成两堆（n_clusters=2）！”

电脑会做两件事：

最后，电脑会给我们两个结果：

1. 猜中心：先随便猜两个位置作为 “堆中心”。
2. 迭代调整：
  1. 把每个水果分配到离它最近的 “堆中心”。
  2. 根据新分配的水果，重新计算 “堆中心” 的位置。
  3. 重复这个过程，直到 “堆中心” 不再变化（或变化很小）。
3. labels：每个水果属于哪一堆（0 或 1）。
4. centers：两堆水果的 “中心坐标”（就像每堆水果的 “重心”）。

第三步：可视化结果（用图展示 “分堆效果”）

# 可视化聚类结果

plt.figure(figsize=(10, 6))

plt.scatter(X[labels == 0, 0], X[labels == 0, 1], c='blue', label='Cluster 1')

plt.scatter(X[labels == 1, 0], X[labels == 1, 1], c='red', label='Cluster 2')

plt.scatter(centers[:, 0], centers[:, 1], c='black', s=200, alpha=0.7, label='Centroids')

plt.title('K-means Clustering Results (k=2)')

plt.xlabel('X')

plt.ylabel('Y')

plt.legend()

plt.grid(True)

plt.show()

说明：

这段代码就像画了一张 “水果分堆地图”：

1. 蓝色点：电脑认为属于第一堆的水果（可能是苹果）。
2. 红色点：电脑认为属于第二堆的水果（可能是橘子）。
3. 黑色大圆点：两堆水果的 “中心位置”（就像在每堆水果中间插了一面旗子）。

第四步：打印聚类中心（看看电脑分堆的 “准确度”）

# 打印聚类中心坐标

print("聚类中心坐标:")

for i, center in enumerate(centers):

print(f"簇 {i+1}: ({center[0]:.4f}, {center[1]:.4f})")

说明：

我们对比一下电脑找到的 “堆中心” 和我们一开始设定的位置：

1. 我们最初设定的中心是 (2, 2) 和 (-2, -2)。
2. 电脑找到的中心会非常接近这两个值（比如 (1.9, 1.8) 和 (-1.9, -1.8)）。

如果电脑分堆分得好，这两个值应该很接近！

K-means 的 “魔法” 与 “陷阱”

魔法：K-means 能自动找到数据中 “自然聚集” 的模式，不需要告诉它 “苹果长啥样” 或 “橘子长啥样”，只要数据确实存在不同的 “堆”，它就能发现。
陷阱：
1. 你必须提前告诉它要分几堆（k=2）。如果设错了（比如设成 k=3），结果会很奇怪。
2. 如果数据不是明显分成几堆（比如所有水果混在一起），K-means 可能会强行分堆，结果就不准确了。