当前位置：首页 > news >正文

深度学习-参数初始化、损失函数

news 2025/7/16 5:15:32

A、参数初始化

参数初始化对模型的训练速度、收敛性以及最终的性能产生重要影响。它可以尽量避免梯度消失和梯度爆炸的情况。

一、固定值初始化

在神经网络训练开始时，将权重或偏置初始化为常数。但这种方法在实际操作中并不常见。

1.1全零初始化

将所有的权重参数初始化为0，但此时模型在每一层神经元上就无法学习，把所有的特征信息都忽略了，但模型仍然会接收输入数据，由于所有神经元的权重相同，它们会对所有输入做相同的响应。

全零初始化可以用来初始化偏置。

API：import torch.nn as nn

nn.init.zeros_(linear.weight)

代码示例：

import torch
import torch.nn as nn
def test01():linear = nn.Linear(in_features = 6 , out_features = 4)nn.init.zeros_(linear.weight)print(linear.weight)
if __name__ == '__main__':test01()

结果：

Parameter containing:
tensor([[0., 0., 0., 0., 0., 0.],
[0., 0., 0., 0., 0., 0.],
[0., 0., 0., 0., 0., 0.],
[0., 0., 0., 0., 0., 0.]], requires_grad=True)

1.2全一初始化

只是把值从群全部为0，转换为全为1。

代码：

import torch
import torch.nn as nn
def test02():linear = nn.Linear(in_features = 3,out_features = 2)nn.init.ones_(linear.weight)print(linear.weight)
if __name__ == '__main__':test02()

结果：

Parameter containing:
tensor([[1., 1., 1.],
[1., 1., 1.]], requires_grad=True)

1.3任意常数初始化

将参数设为非零的常数。要自行设置这个非零数字。

代码：

def test03():linear = nn.Linear(in_features = 2,out_features = 4)nn.init.constant_(linear.weight,7.7)print(linear.weight)
if __name__ == '__main__':test03()

结果：

Parameter containing:
tensor([[7.7000, 7.7000],
[7.7000, 7.7000],
[7.7000, 7.7000],
[7.7000, 7.7000]], requires_grad=True)

1.4固定值初始化

将权重的参数数值自定义下来，在整个程序中它都一直保持这个数值不变。

代码：

def test04():net = nn.Linear(2,2,bias=True)x = torch.tensor([[0.1,0.95]])net.weight.data = torch.tensor([[0.1,0.2],[0.3,0.4]])output = net(x)print(output)print(net.weight)print(net.bias)if __name__ == '__main__':test04()

结果：

tensor([[-0.2744, 0.0352]], grad_fn=<AddmmBackward0>)

Parameter containing:
tensor([[0.1000, 0.2000],
[0.3000, 0.4000]], requires_grad=True)
Parameter containing:
tensor([-0.4744, -0.3748], requires_grad=True)

二、随机初始化

将权重初始化为随机的小值，通常呈现正态分布或者均匀分布。

它可以避免对称性破坏，但是可能会出现梯度消失（权重太小）或者梯度爆炸（权重太大）。

注：“对称性破坏”（Symmetry Breaking）是指：如果神经网络中所有参数（例如同一层的权重）被初始化为相同的值（比如全0或者全相同的非零值），那么在训练过程中，这些参数会以相同的方式更新，导致同一层中的所有神经元在训练过程中学习到相同的特征。这样，这些神经元在功能上就是冗余的，整个网络的表达能力就会受到限制，相当于只有一个神经元的效果。

API：

均匀分布随机初始化：nn.init.uniform_(linear.weight)

正态分布随机初始化：nn.init.normal_(linear.weight)

代码：

import torch.nn as nn
def test():linear = nn.Linear(2,3)fun1 = nn.init.uniform_(linear.weight)print(fun1)fun2 = nn.init.normal_(linear.weight,mean=0,std=1)print('-'*40)print(fun2)if __name__ == '__main__':test()

结果：

Parameter containing:
tensor([[0.7598, 0.4357],
[0.3120, 0.3512],
[0.6281, 0.1598]], requires_grad=True)
----------------------------------------
Parameter containing:
tensor([[ 1.0969, 0.5326],
[-0.0624, 1.1465],
[ 0.0963, 0.1332]], requires_grad=True)

三、Xavier初始化

泽维尔初始化也叫做Glorot初始化，核心原理是跟如输入输出的维度来初始化权重，使得每一层的输出方差保持一致：主要是前向传播的方差一致性和反向传播的梯度方差一致性。综合考虑之下，为了同时平衡前向传播和反向传播，Xavier采用的权重为Var(W) = 2/(Nin+Nout)

API：

均匀分布：nn.init.xavier_uniform_(linear.weight)

正态分布：nn.init.xavier_normal_(linear.weight)

代码：

def test06():linear1 = nn.Linear(3,4)nn.init.xavier_uniform_(linear1.weight)print(linear1.weight)linear2 = nn.Linear(3,2)nn.init.xavier_normal_(linear1.weight)print(linear2.weight)if __name__ == '__main__':test06()

结果：

Parameter containing:
tensor([[-0.2246, -0.2905, 0.4308],
[ 0.2819, 0.6478, -0.5633],
[ 0.3807, -0.7230, -0.2279],
[-0.6118, -0.0948, 0.4442]], requires_grad=True)
Parameter containing:
tensor([[ 0.4279, -0.1615, -0.0495],
[ 0.1024, 0.4124, 0.2298]], requires_grad=True)

四、He初始化

He初始化也叫kaiming初始化，核心思想是调整权重的初始化范围，使得每一层的输出方差保持一致（前向传播的方差一致性、反向传播的梯度一致性）。它是专门针对ReLU激活函数进行优化的。分为两种模式：

（1）fan_in：优先保证前向传播稳定，方差2/Nin;

（2）fan_out:优先保证反向传播稳定，方差2/Nout;

api : nn.init_kaiming_uniform(linear.weight)

nn.init_kaiming_normal(linear.weight)

代码:

def test08():linear = nn.Linear(1,4)nn.init.kaiming_uniform_(linear.weight)print(linear.weight)linear = nn.Linear(2,1)nn.init.kaiming_normal_(linear.weight)print(linear.weight)if __name__ == '__main__':test08()

结果：

Parameter containing:
tensor([[ 1.2009],
[-0.5195],
[-0.3154],
[ 1.0753]], requires_grad=True)
Parameter containing:
tensor([[ 1.1605, -0.8621]], requires_grad=True)

五、小结

自此，在前边学习了四种对权重初始化的方法，每个网络层的参数都有默认的初始化方法，同时对上面的方法我们也要针对具体情况进行使用。

B、损失函数

一、线性回归损失函数

1.1MAE损失

MAE平均绝对误差，L1-Loss，通过对预测值和真实值之间的绝对差来衡量他们之间的差异。

特点：

（1）鲁棒性强，比MSE鲁棒性好，他不会像MSE那样对较大误差平方敏感；

（2）物理意义直观。

API：nn.L1Loss()

代码：

import torch
import torch.nn as nndef test1():mae_loss = nn.L1Loss()y_pred = torch.tensor([0.4,2.3])y_true = torch.tensor([0.5,2.2])loss = mae_loss(y_pred,y_true)print(loss.item())if __name__ == '__main__':test1()

结果：

0.09999994933605194

1.2MSE损失

均方差损失，L2Loss，通过对预测值和真实值之间的误差平方取平均值，来衡量预测值与真实值之间的差异。

特点：

（1）平方惩罚，对误差施加更大的惩罚，对异常值更为敏感；

（2）凸性：MSE是一个凸函数，它具有一个唯一的全局最小值，有助于优化问题的求解。

API：nn.MSELoss()

代码：

mse_loss = nn.MSELoss()
y_true = torch.tensor([0.9,2.1])
y_pred = torch.tensor([0.7,2.2])
loss = mse_loss(y_true,y_pred)
print(loss.item())

结果：

0.025000011548399925

二、交叉熵

用于分类。

2.1信息量

信息量用于衡量一个事件所包含的信息的多少。信息量的定义基于事件发生的概率：事件发生的概率越低，其信息量越大。

公式：

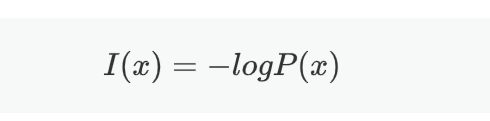
其中x为某一事件，p(x)是该事件发生的概率，I(x)是该事件的信息量。

2.2信息熵

信息熵是信息量的期望值，熵越大，表示事件的不确定性越大。

2.3KL散度

KL散度用于衡量两个概率分布之间的差异（损失的信息量），KL越小，两个分布越接近。

2.4交叉熵

在KL散度的基础上，将KL公式展开，就能得到交叉熵。

注意：

交叉熵函数内置了softmax，所以不要重复显示调用softmax。CrossEntropyLoss是多分类问题的首选损失函数

所以，CrossEntropyLoss 实质上是两步的组合：Cross Entropy = Log-Softmax + NLLLoss

Log-softmax：是对softmax函数取对数；

NLLLoss：对Log-softmax取负值。

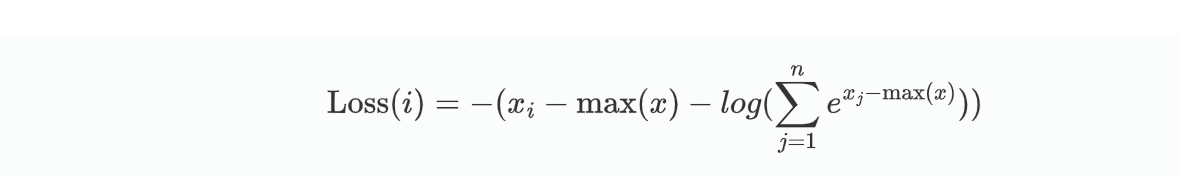
利用交叉熵进行分类：

（1）输入数据信息；

（2）输入真实标签的数据；

（3）定义损失函数；

（4）定义loss,将输入信息代入损失函数；

（5）查看结果。

代码：

import torch
import torch.nn as nn
input_data = torch.tensor([[1.5,2.0,0.5],[0.5,1.0,1.5]])  #分别对应类别 0、1 和 2 的得分
labels = torch.tensor([1,2])
criterion = nn.CrossEntropyLoss()
loss = criterion(input_data,labels)
print('交叉熵损失为：',loss.item())

结果：

交叉熵损失为： 0.6422001123428345

三、二分类交叉熵

在输出层使用sigmoid激活函数进行二分类时运用该损失函数。

二分类问题的标签只有两个，要么0，要么1，因此原本的损失函数可以写为：

代码：

def test001():y = torch.tensor([[0.7],[0.2],[0.9],[0.7]])#信息为相应分类的概率labels = torch.tensor([[1],[0],[1],[0]],dtype = torch.float)#对应信息的标签bceloss = nn.BCELoss()loss = bceloss(y,labels)print('二分类交叉熵的损失值为：',loss.item())if __name__ == '__main__':test001()

结果：

二分类交叉熵的损失值为： 0.47228795289993286