机器学习之逻辑回归和k-means算法(六)
机器学习之逻辑回归和k-means算法(六)
文章目录
- 机器学习之逻辑回归和k-means算法(六)
- 一、 逻辑回归
- 1.概念
- 2.原理
- 3.API
- 4.案例
- 二、 无监督学习 & K-means 聚类算法详解(通俗易懂版)
- 1.什么是无监督学习?
- 2.聚类算法是什么?
- 聚类 vs 分类的区别:
- 3.K-means 聚类算法详解
- 3.1. 什么是“簇”和“质心”?
- 3.2. K-means 算法的步骤(通俗易懂版):
- 动态图示(帮助理解):
- 4.总结一句话:
- 5.K-means 的应用场景
- 6.案例
一、 逻辑回归
1.概念
逻辑回归(Logistic Regression)是机器学习中的一种分类模型,逻辑回归是一种分类算法,虽然名字中带有回归,但是它与回归之间有一定的联系。由于算法的简单和高效,在实际中应用非常广泛。
逻辑回归一般用于二分类问题,比如:
是好瓜还是坏瓜
健康还是不健康
可以托付终身还是不可以
2.原理
逻辑回归的输入是线性回归的输出
线性回归: h(w)=w1x1+w2x2+....+bh(w)=w_1x_1+w_2x_2+....+bh(w)=w1x1+w2x2+....+b
sigmoid激活函数 :f(x)=11+e−xf(x)=\frac{1}{1+e^{-x}}f(x)=1+e−x1
sigmoid函数的值是在[0,1]区间中的一个概率值,默认为0.5为阈值可以自己设定,大于0.5认为是正例,小于则认为是负例
把上面的h(w)h(w)h(w) 线性的输出再输入到sigmoid函数当中 f(w)=11+e−h(w)f(w)=\frac{1}{1+e^{-h(w)}}f(w)=1+e−h(w)1

3.API
逻辑斯蒂
sklearn.linear_model.LogisticRegression()
参数:fit_intercept bool, default=True 指定是否计算截距max_iter int, default=100 最大迭代次数。迭代达到此数目后,即使未收敛也会停止。
模型对象:.coef_ 权重.intercept_ 偏置predict()预测分类predict_proba()预测分类(对应的概率)score()准确率
4.案例
from sklearn.datasets import load_iris
from sklearn.linear_model import LogisticRegression
from sklearn.model_selection import train_test_splitiris = load_iris()
x = iris.data
y = iris.target
x_train, x_test, y_train, y_test = train_test_split(x, y, test_size=0.2)model = LogisticRegression(max_iter=1000,fit_intercept=False) # 设置最大迭代次数 避免警告
model.fit(x_train, y_train)
print(model.coef_) #w
print(model.intercept_) # by_predict = model.predict(x_test)
print(y_predict)
print(y_test)
print(model.score(x_test, y_test))
运行结果:

二、 无监督学习 & K-means 聚类算法详解(通俗易懂版)
在机器学习的世界里,我们经常会听到“监督学习”和“无监督学习”这两个词。今天我们就来聊聊其中的 无监督学习,以及它里面非常经典的一个算法 —— K-means 聚类算法。
1.什么是无监督学习?
简单来说:
- 无监督学习就是让计算机自己从数据里找规律,不需要我们提前告诉它“正确答案”。
- 它只需要数据的特征(比如年龄、收入、消费频率等),不需要标签(比如“用户是否流失”)。
- 最常见的无监督学习任务就是 聚类,也就是把相似的数据自动分到一组。
2.聚类算法是什么?
聚类算法的核心思想是:
- 把数据分成若干个“簇”(cluster),每个簇里的数据彼此相似,不同簇之间的数据差异大。
- 目标是:簇内差异小,簇外差异大。
- 差异通常是通过“距离”来衡量的,比如欧氏距离。
聚类 vs 分类的区别:
| 项目 | 聚类(无监督) | 分类(监督学习) |
|---|---|---|
| 是否有标签 | ❌ 没有标签 | ✅ 有标签 |
| 目标 | 自动分组 | 预测类别 |
| 应用场景 | 用户分群、图像分割等 | 垃圾邮件识别、疾病预测等 |
3.K-means 聚类算法详解
K-means 是最常用的聚类算法之一,它的目标是把数据分成 K 个簇,让簇内的数据点尽可能“抱团”。
3.1. 什么是“簇”和“质心”?
- 簇:就是一组相似的数据点,算法会把它们归为一类。
- 质心:就是每个簇的“中心点”,是这个簇中所有点的平均值。
3.2. K-means 算法的步骤(通俗易懂版):
- 随机选 K 个点作为初始质心(可以随便选)。
- 把每个数据点分配给最近的质心,形成 K 个簇。
- 重新计算每个簇的质心(就是簇内所有点的平均值)。
- 重复步骤 2 和 3,直到质心不再变化(或者变化很小),就停止。
动态图示(帮助理解):
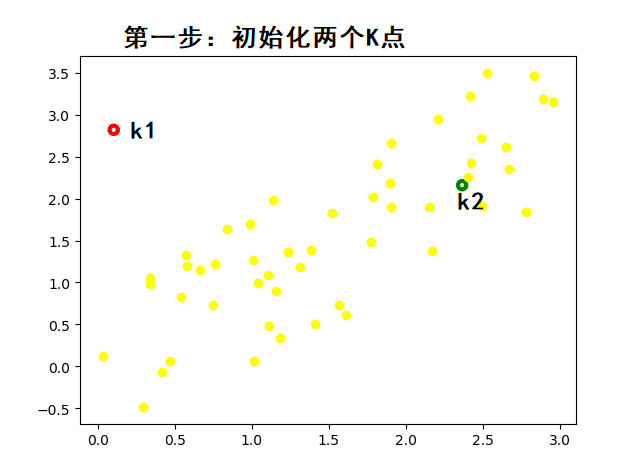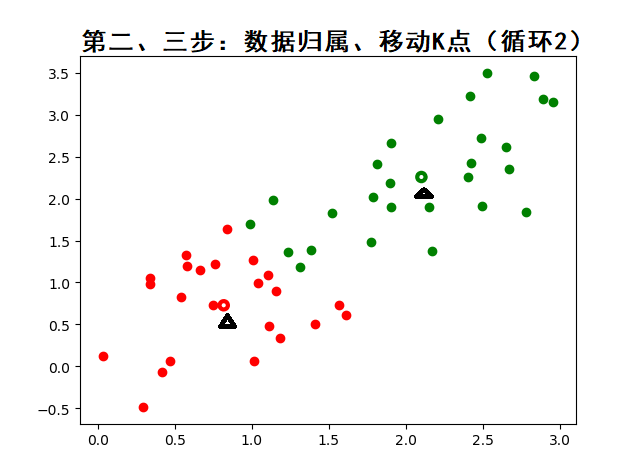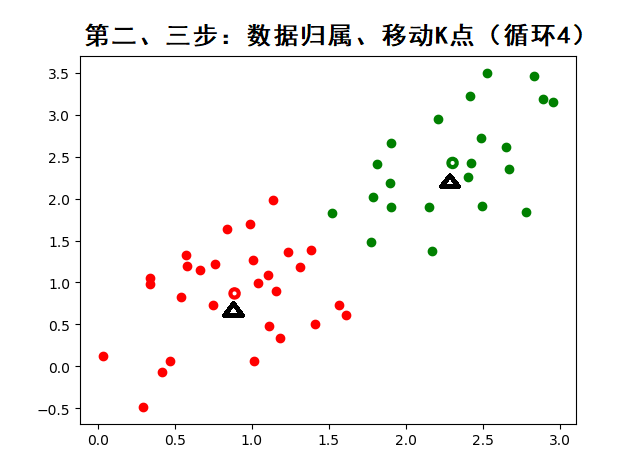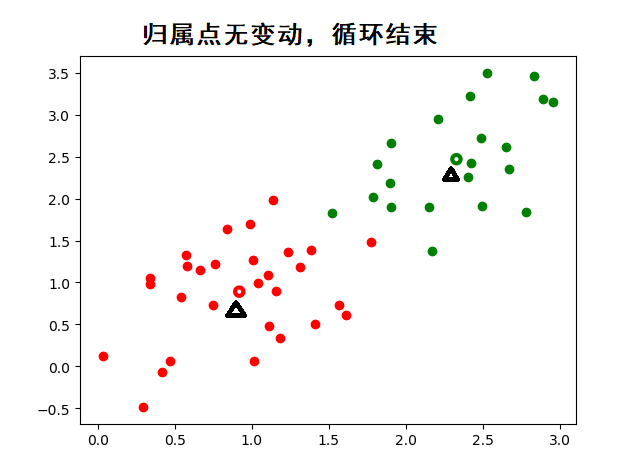
4.总结一句话:
K-means 就是一个不断“找中心、分数据、再重新找中心”的过程,直到数据分组稳定下来。
5.K-means 的应用场景
- 用户画像与分群
- 图像压缩与分割
- 文档聚类
- 市场细分
6.案例
from sklearn.cluster import KMeans
import numpy as np
import matplotlib.pyplot as plt# 设置随机种子
np.random.seed(0)# 生成随机数据
data = np.random.rand(1000, 2) # 生成形状为 (1000, 2) 的随机数组# 使用 KMeans 进行聚类
kmeans = KMeans(n_clusters=5) # 指定聚类中心数量为 5
kmeans.fit(data) # 拟合数据# 输出聚类结果
print("Cluster labels:", kmeans.labels_) # 聚类标签
print("Cluster centers:\n", kmeans.cluster_centers_) # 聚类中心
print("Inertia:", kmeans.inertia_) # 聚类的惯性(SSE)# 可视化结果
plt.scatter(data[:, 0], data[:, 1], c=kmeans.labels_) # 绘制数据点
plt.scatter(kmeans.cluster_centers_[:, 0], kmeans.cluster_centers_[:, 1], s=100, c='red') # 绘制聚类中心
plt.show()
运行结果:


如果你觉得这篇文章对你有帮助,欢迎点赞、收藏、转发!🎯
