傅里叶变换理解

首先来看看然人颤抖的傅里叶变换公式：

着实棘手
开始破解之旅：
以时间作为参照来观察动态世界的方法我们称其为时域分析。而我们也想当然的认为，世间万物都在随着时间不停的改变，并且永远不会静止下来。
然而用另一种方法来观察世界的话，你会发现世界是永恒不变的，这个静止的世界就叫做频域。（历史总是惊人的相似）
关键理解：
傅里叶同学告诉我们，任何周期函数，都可以看作是不同振幅，不同相位正弦波的叠加。
欧拉公式：在数学领域的意义要远大于傅里叶分析。

当x等于 Pi 的时候，就变成了它

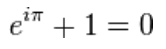
常用用途：
1.求解微分方程，微分方程是指含有未知函数及其导数的关系式。解微分方程就是找出未知函数。
求解微分方程除了要计算加减乘除，还要计算微分积分。而傅里叶变换则可以让微分和积分在频域中变为乘法和除法，大学数学瞬间变小学算术。
2.信号滤波，从曲线中去除一些特定的频率成分，工程上称为滤波；在时域基本无解，但在频域能轻松做到，无非就是删除几条竖线而已。