网络安全基础：从CIA三元组到密钥交换与消息认证

网络安全基础：从CIA三元组到密钥交换与消息认证

欢迎来到网络安全的奇妙世界！如果你曾对那些黑客电影里的炫酷操作感到好奇，或者对“数据泄露”、“账户被盗”这类新闻感到担忧，那么这篇博客就是为你准备的。网络安全听起来可能高深莫测，但它的核心理念和技术，其实比你想象的要贴近生活，也更容易理解。

今天，我们将一起踏上一段探索之旅，从网络安全最根本的追求——CIA三元组开始，逐步揭开对称加密、非对称加密的神秘面纱，看看它们是如何在像HTTPS这样的日常应用中协同工作的，最后我们还会探讨如何确保我们收到的信息是真实可信且未被篡改的。

网络安全的基石：CIA三元组的奥秘

在我们深入探讨各种酷炫的加密技术之前，首先要明白我们为什么要搞网络安全？我们到底想保护什么？答案可以概括为三个核心目标，它们在网络安全领域被称为“CIA三元组”（CIA Triad）。这里的CIA可不是美国中央情报局，而是三个英文单词的首字母缩写：Confidentiality（机密性）、Integrity（完整性）和Availability（可用性）。不过，根据你提供的资料，我们今天主要聚焦在前两个以及与之紧密相关的Authentication（认证）。所以，我们重点讨论机密性、完整性、认证这三个与你问题相关的核心概念。

机密性 (Confidentiality)：保守你的秘密

想象一下，你写了一封情书，或者一份商业合同，你肯定不希望除了指定的收件人之外，任何人能看到里面的内容。这就是机密性。

• 定义： 机密性确保信息不被泄露给未经授权的个人、实体或进程。简单来说，就是“保守秘密”，防止信息落入坏人之手。
• 重要性： 在数字世界，我们的个人信息、银行账户、商业机密、国家机密等，都需要机密性来保护。如果你的网上银行密码被泄露（失去了机密性），后果不堪设想。如果公司的核心研发资料被竞争对手获取，那将是灾难性的。
• 如何实现： 加密是实现机密性的主要手段。通过加密算法，可以将原始信息（明文）转换成一堆乱码（密文），只有拥有正确密钥的人才能将其还原成可读的明文。我们后面会详细讲加密。

【图1：机密性概念图】

完整性 (Integrity)：确保信息未被篡改

现在，假设你的情书安全地送到了对方手中，对方也成功打开了。但是，如果信的内容在传递过程中被偷偷修改了呢？比如“我喜欢你”被改成了“我讨厌你”，那误会可就大了。这就是完整性要解决的问题。

• 定义： 完整性要求在数据的整个生命周期中，保持其一致性、准确性和可信度。简单说，就是“防止未经授权的篡改”，确保你收到的信息就是发送方发出的原始信息，一字不差。
• 重要性： 想象一下，你下载一个软件更新，如果这个更新包在下载过程中被黑客植入了恶意代码（破坏了完整性），你的电脑就可能被控制。银行转账时，如果转账金额从100元被篡改成10000元，那也是完整性被破坏的体现。
• 如何实现： 主要通过哈希函数（Hash Functions）和消息认证码（MACs，我们后面会详细讲）等技术来实现。这些技术可以为数据生成一个独特的“指纹”，如果数据有任何微小的变动，这个“指纹”就会完全不同。

【图2：完整性概念图】

认证 (Authentication)：验明你的正身

好了，现在信息既保密又完整地送达了。但还有一个问题：你怎么确定发信人真的是你以为的那个人呢？万一是有人冒充你的名义发的呢？或者，当服务器收到一个请求时，它怎么知道这个请求真的是来自合法的你，而不是一个攻击者呢？这就是认证的作用。

• 定义： 认证是验证用户、进程或设备的身份，以授予对资源的访问权限的过程。简单说，就是“确保‘你’是你所声称的‘你’”。
• 重要性： 你登录邮箱需要输入用户名密码，这就是一种认证。ATM机需要你插入银行卡并输入密码，也是认证。如果没有认证，任何人都可以冒充他人访问敏感信息或执行未授权操作。
• 如何实现： 方法多种多样，包括：
  • 你知道什么：密码、PIN码。
  • 你拥有什么：智能卡、USB Key、手机验证码。
  • 你是什么（生物特征）：指纹、人脸识别、虹膜扫描。
  • 在网络通信中，数字签名和我们后面会讲到的消息认证码（MACs）也扮演着重要的认证角色。

这三个特性——机密性、完整性、认证——是构建安全系统的基石。它们常常是相辅相成的。例如，你希望你的银行交易是机密的（不被别人看到金额），是完整的（金额不被篡改），并且银行能认证你的身份才允许你操作。

速记： 网络安全三要素（根据你的问题调整）：机密性（保守秘密）、完整性（防止篡改）、认证（验明正身）。

对称密钥加密：一把钥匙锁天下

现在我们知道了“机密性”的重要性，那么如何实现它呢？最常用的方法就是加密 (Cryptography)。加密技术有很多种，我们先从一种基础且高效的加密方式开始：对称密钥加密 (Symmetric Key Cryptography)。

什么是对称密钥加密？

想象一下，你和你的朋友约定使用同一个保险箱和同一把钥匙。你要给朋友寄一件秘密物品，你会：

1. 把物品放进保险箱。
2. 用你们共享的那把钥匙锁上保险箱。
3. 把锁上的保险箱寄给朋友。
   朋友收到后：
4. 用同一把钥匙打开保险箱。
5. 取出秘密物品。

在这个过程中，“同一把钥匙” 是关键。

在对称密钥加密中：

• 加密和解密使用完全相同的密钥。
• 发送方（比如叫Alice）和接收方（比如叫Bob）必须在通信之前，通过某种安全的方式共享这个密钥。
• Alice用这个共享密钥将原始信息（称为明文 Plaintext $P_t$）转换成加密后的信息（称为密文 Ciphertext $C_t$）。
• Bob收到密文后，用完全相同的共享密钥将密文还原成原始的明文。

【图3：对称密钥加密流程图】

上图清晰地展示了这个过程：

1. 密钥共享 (Key Sharing): Alice 和 Bob 必须事先安全地共享密钥 $k$。这是对称加密的一个核心挑战，我们稍后会讨论。
2. 加密 (Encryption): Alice 使用共享密钥 $k$ 和加密算法 $E$ 将明文 $P_t$ 加密成密文 $C_t$。可以表示为：$C_t=E_k(P_t)$。
3. 传输 (Transmission): 密文 $C_t$ 通过可能不安全的信道（比如互联网）发送给 Bob。
4. 解密 (Decryption): Bob 收到密文 $C_t$ 后，使用完全相同的密钥 $k$ 和解密算法 $D$ 将其解密回原始明文 $P_t$。可以表示为：$P_t=D_k(C_t)$。

对称加密的数学表达（以凯撒密码为例简化理解）

对称加密算法有很多种，比如DES、3DES、AES等。它们的数学原理比较复杂。为了方便理解，我们可以用一个非常古老和简单的对称加密例子——凯撒密码（Caesar Cipher）的思想，结合你提供的公式来理解其核心运算。

假设我们的明文和密钥都是英文字母，我们可以给每个字母编一个号（A=0, B=1, …, Z=25）。字母表的大小 $N_a$ 就是26。
设 $P(i)$ 是明文中第 $i$ 个字符对应的数字， $K(i)$ 是密钥中第 $i$ 个字符对应的数字（如果密钥比明文短，可以循环使用密钥）， $C(i)$ 是密文中第 $i$ 个字符对应的数字。

• 加密过程：
  $$C(i)=(P(i)+K(i))(\mathrm{mod}{N}_a)$$
  这里的 $(\mathrm{mod}{N}_a)$ 表示取模运算，即将 $P(i)+K(i)$ 的结果除以 $N_a$ 后取余数。这确保了结果仍然在 $0$ 到 $N_a-1$ 的范围内，对应于字母表中的一个字母。
  例如，明文是 ‘H’ (7)，密钥是 ‘C’ (2)，字母表大小是 26。
  $C=(7+2)(\mathrm{mod}26)=9(\mathrm{mod}26)=9$。数字9对应字母 ‘J’。所以 ‘H’ 被加密成了 ‘J’。

• 解密过程：
  $$P(i)=(C(i)-K(i))(\mathrm{mod}{N}_a)$$
  同样，用上面的例子，密文是 ‘J’ (9)，密钥是 ‘C’ (2)。
  $P=(9-2)(\mathrm{mod}26)=7(\mathrm{mod}26)=7$。数字7对应字母 ‘H’。成功解密！

注意： 真正的现代对称加密算法（如AES）比这个复杂得多，它们涉及多轮的替换、置换等操作，但核心思想都是用一个密钥进行可逆的数学变换。你提供的公式是一种非常简化的加法模式的对称加密表示。

速记： 对称加密：加密解密用同一把密钥。公式上，加密是加法（或其它运算）取模，解密是减法（或其逆运算）取模。

对称加密的弱点：密钥分发问题

对称加密算法本身可以非常强大，加密速度也快。但它有一个致命的弱点，也是它的根本问题——密钥分发 (Key Distribution)。

• 问题描述： 如何让通信双方（比如从未见过面的Alice和Bob）在开始加密通信之前，安全地共享那个唯一的秘密密钥呢？
  • 如果他们通过一个不安全的信道（比如普通的电子邮件、电话）直接发送密钥，那么任何窃听者（比如Eve）都能截获这个密钥。一旦密钥泄露，对称加密就形同虚设，因为Eve也能用同样的密钥解密他们的所有通信了。
  • 如果他们有安全的信道，那为什么不直接用那个安全信道通信呢？这似乎陷入了一个“鸡生蛋还是蛋生鸡”的困境。

这个问题非常关键。如果密钥不能安全地分发，那么再强大的对称加密算法也白搭。这就好比你有一个世界上最坚固的保险箱，但你把钥匙大摇大摆地放在门口，那保险箱还有什么用呢？

速记： 对称加密的根本问题：如何安全地把那把唯一的密钥交给对方。

柳暗花明：公钥密码体制与HTTPS中的密钥共享

对称加密的密钥分发问题困扰了密码学家很久。直到上世纪70年代，一种革命性的思想出现了，那就是公钥密码体制 (Public Key Cryptography)，也叫非对称加密 (Asymmetric Cryptography)。它巧妙地解决了对称密钥分发的部分难题。

公钥密码体制简介

与对称加密只有一把密钥不同，非对称加密有两把密钥：

• 公钥 (Public Key)： 这把密钥是公开的，任何人都可以获取。就像你的邮箱地址一样，可以告诉任何人。
• 私钥 (Private Key)： 这把密钥是保密的，只有密钥的拥有者自己知道，绝不能泄露。就像你的邮箱密码一样。

这两把密钥是数学上相关的，用公钥加密的信息只能用对应的私钥解密；反之，用私钥签名（一种特殊形式的加密）的信息可以用公钥验证。

关键特性：

1. 知道公钥，很难推导出私钥。
2. 用一把密钥加密，必须用另一把密钥解密。

这种机制是如何帮助解决对称密钥分发问题的呢？我们来看看在实际应用中，比如我们每天都在用的HTTPS（安全的网页浏览协议），它是怎么做的。

HTTPS中对称密钥的共享艺术

HTTPS的目标是让我们在浏览器和网站服务器之间的通信变得安全（机密、完整、可认证）。它并不是完全依赖非对称加密，因为非对称加密虽然解决了密钥分发，但计算开销大，速度比对称加密慢很多。所以，HTTPS采用了一种混合策略：

1. 使用非对称加密来安全地“协商”或“交换”一个对称密钥。
2. 一旦双方都有了这个对称密钥，后续的大量数据传输就使用高效的对称加密。

这个过程通常发生在TLS/SSL握手阶段（TLS是HTTPS的底层安全协议）：

• 第一步：服务器亮出“身份”和“公开信箱”

  • 当你的浏览器（客户端）尝试连接一个HTTPS网站（服务器）时，服务器会发送它的数字证书给浏览器。
  • 这个证书里包含了服务器的公钥，以及由权威机构（CA，Certificate Authority）对这个公钥和服务器身份的认证。浏览器会验证这个证书的有效性。

• 第二步：客户端生成“一次性密码本”并锁好

  • 浏览器验证证书通过后，会生成一个随机的、全新的对称密钥。这个密钥通常被称为会话密钥 (Session Key)，因为它只用于本次通信会话。
  • 浏览器会使用从服务器证书中获取到的服务器公钥，来加密这个刚刚生成的会话密钥。

• 第三步：客户端发送“加密的密码本”

  • 浏览器将这个被服务器公钥加密后的会话密钥发送给服务器。

• 第四步：服务器用“私藏钥匙”打开

  • 服务器收到这个加密的会话密钥后，使用它自己的私钥进行解密。因为只有服务器拥有这个私钥，所以只有它能成功解密，从而得到浏览器生成的那个会话密钥。
  • 即使有攻击者在中间窃听，它截获到的也只是被服务器公钥加密的会话密钥。由于攻击者没有服务器的私钥，它无法解密得到真正的会话密钥。

• 安全通道建立！

  • 至此，浏览器和服务器双方都拥有了同一个会话密钥（对称密钥）。
  • 之后，它们之间所有的通信数据（比如你请求的网页内容、你提交的表单信息）都会使用这个会话密钥进行对称加密和解密。因为对称加密速度快，非常适合大量数据的传输。

【图4：HTTPS中密钥交换简化流程】
(客户端生成session key，用服务器公钥加密，发送给服务器，服务器用私钥解密得到session key，然后双方用session key对称加密通信)

总结一下HTTPS中密钥共享的精髓：

• 非对称加密（公钥/私钥）用来解决对称加密的密钥（会话密钥）的安全分发问题。
• 对称加密（会话密钥）用来进行后续高效的数据加密通信。
• 这是一个“用大炮打蚊子不划算，但用大炮安全地运送高效的苍蝇拍很划算”的逻辑。

速记： HTTPS中，用非对称加密（公钥加密）来安全地传输对称加密的密钥（会话密钥）。

公钥加密的“定海神针”：数学难题

你可能会问，为什么知道了公钥就推算不出私钥呢？这听起来有点神奇。公钥加密的安全性，正是建立在一些经过长期研究、被认为是计算上非常困难的数学问题之上的。

• 对于RSA算法（一种广泛使用的公钥加密算法）：

  • 其安全性基于大整数分解问题 (Integer Factorization Problem) 的难度。
  • 简单来说，给你两个非常大的质数，把它们乘起来很容易。但是，反过来，给你一个巨大的合数（由两个大质数相乘得到），让你找出最初的那两个质数因子，则非常非常困难，对于目前已知的最快算法和计算机来说，如果数字足够大（比如2048位或更大），这需要天文数字般的时间。RSA的公钥包含这个大合数，私钥则包含那两个质数因子。

• 对于Diffie-Hellman密钥交换协议和ElGamal加密算法等：

  • 它们的安全性依赖于离散对数问题 (Discrete Logarithm Problem)。
  • 在一个特定的数学结构（有限域或椭圆曲线群）中，计算 $g^x(\mathrm{mod}p)$ 很容易（已知 $g,x,p$），但反过来，已知 $g,p$ 和 $g^x(\mathrm{mod}p)$ 的结果，想要求出 $x$ 则非常困难。

这些数学难题就像是公钥加密的“定海神针”，只要这些问题在计算上仍然是“难解”的，公钥加密体系的安全性就能得到保障。当然，随着计算技术（比如量子计算）的发展，这些难题的难度可能会发生变化，密码学家们也在不断研究新的抗量子计算的加密算法。

速记： 公钥加密的安全性依赖于数学难题，如大整数分解或离散对数。

消息的“身份证”与“防伪标”：消息认证码 (MAC)

我们已经讨论了如何实现机密性（加密）和如何安全地交换加密密钥。现在，我们回到CIA三元组的另外两个重要成员：完整性 (Integrity) 和 认证 (Authentication)。如何确保我们收到的消息确实来自声称的发送者，并且在传输过程中没有被篡改呢？

简单的身份验证为何不可靠？MAC地址的陷阱

在一些物联网(IoT)场景或其他简单网络中，工程师有时可能会想用一些看似简单的方法来验证数据来源，比如使用设备的MAC地址 (Media Access Control Address)。MAC地址是网卡硬件的物理地址，理论上是唯一的。

想法： 如果我收到一个数据包，声称来自某个传感器，我检查一下数据包的源MAC地址，如果是我已知的那个传感器的MAC地址，我就认为数据是可信的。

问题： 这种方法存在严重的安全漏洞！

• MAC地址可以被轻易地伪造 (Spoofed)。 攻击者可以很容易地修改自己设备的网络配置，使其发送数据包时声称自己拥有任何它想要的MAC地址。
• 因此，攻击者可以冒充合法的传感器，发送虚假或恶意的数据给接收系统。
• MAC地址本身不提供任何密码学意义上的来源证明或完整性保障。它只是一个网络标识符，不是安全特征。

速记： 用（物理）MAC地址验证身份不可靠，因为MAC地址很容易被伪造。

HMAC：基于哈希的消息认证码

为了真正实现消息的认证和完整性，我们需要更强大的密码学工具。消息认证码 (Message Authentication Code, MAC) 就是为此而生的。其中，一种非常常用且安全的MAC实现方式是 HMAC (Hash-based Message Authentication Code)，即基于哈希函数的消息认证码。

HMAC是如何工作的？

1. 前提：共享密钥。 和对称加密类似，发送方 (Alice) 和接收方 (Bob) 必须事先共享一个秘密密钥 $k_{mac}$。这个密钥专门用于生成和验证MAC，与加密用的密钥可以是同一个，也可以是独立的（推荐独立）。

2. 生成MAC (发送方Alice的操作)：

   • Alice获取要发送的原始消息 $M$。
   • Alice将消息 $M$ 和共享密钥 $k_{mac}$ 一起作为输入，喂给一个密码学哈希函数 (如SHA-256)。
     • 哈希函数是一种单向函数，能将任意长度的输入转换成固定长度的输出（称为哈希值或摘要）。特点是：
       • 同样的输入总能得到同样的输出。
       • 输入有任何微小变化，输出都会截然不同。
       • 从输出很难反推出输入。
   • HMAC的实际计算过程比简单地将消息和密钥拼接后哈希要复杂一些（涉及到内部和外部填充以及两次哈希操作，以抵抗某些攻击），但核心思想是结合消息和密钥生成哈希。
   • 最终得到的这个固定长度的哈希值，就是该消息的MAC码（或称为标签 Tag）。

3. 传输：

   • Alice将原始消息 $M$ 和计算出的MAC码一起发送给Bob。通常是将MAC码附加在消息的末尾。

4. 验证MAC (接收方Bob的操作)：

   • Bob收到消息 $M^{\prime }$ 和附带的MAC码 (Tag’)。
   • Bob使用自己保存的、与Alice共享的那个密钥 $k_{mac}$，以及收到的消息 $M^{\prime }$，通过完全相同的HMAC生成过程（即使用相同的哈希函数和HMAC结构）计算出一个新的MAC码 (Tag’')。

5. 比较与决策：

   • Bob比较自己计算出的MAC码 (Tag’‘) 和从Alice那里收到的MAC码 (Tag’)。
     • 如果 Tag’’ == Tag’： 这意味着：
       1. 认证 (Authentication): 消息确实来自Alice（或者其他任何拥有共享密钥 $k_{mac}$ 的人）。因为只有知道密钥的人才能为这条特定的消息 $M^{\prime }$ 计算出正确的MAC码。攻击者不知道密钥，即使它篡改了消息，也无法生成一个能通过验证的MAC码。
       2. 完整性 (Integrity): 消息在传输过程中没有被篡改。如果消息 $M^{\prime }$ 在途中被哪怕修改了一个比特，Bob用 $M^{\prime }$ 计算出的Tag’’ 就会与Alice原始的Tag’ 完全不同。
     • 如果 Tag’’ != Tag’： 这说明消息要么不是Alice发的，要么在传输过程中被篡改了。Bob应该丢弃这条消息或发出警告。

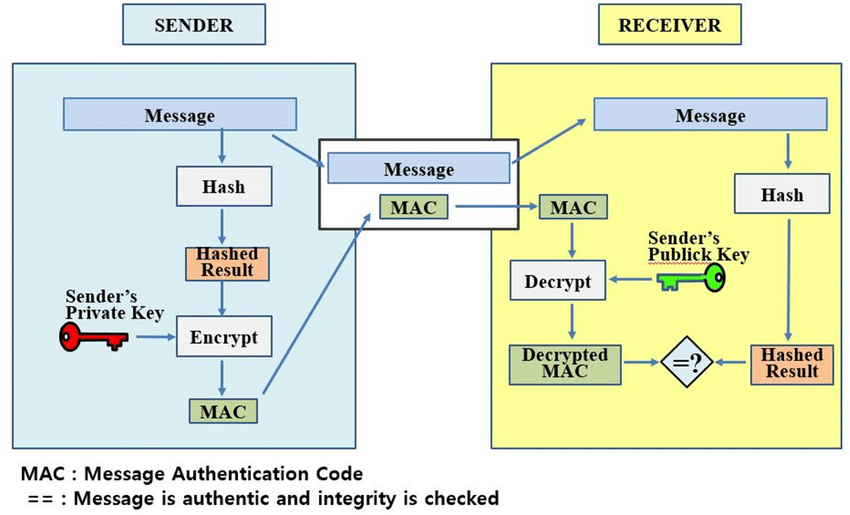
【图5：HMAC工作流程图】
(发送方将Message和Secret Key输入HMAC函数得到MAC，然后将Message+MAC发送出去。接收方收到Message’和MAC’，用Message’和自己的Secret Key输入HMAC函数得到MAC’‘，然后比较MAC’和MAC’'是否相等。)

HMAC的优势：

• 它同时提供了数据来源认证和数据完整性校验。
• 它依赖于哈希函数的单向性和抗碰撞性，以及密钥的保密性。

速记： HMAC验证：发送方用（消息+共享密钥）通过特定哈希运算算出一个MAC码附在消息后；接收方用同样方法（收到的消息+自己的共享密钥）再算一次，对比两个MAC码是否一致。

MAC的用武之地：明文 vs. 密文

生成MAC码时，我们可以选择是对明文消息操作，还是对加密后的密文消息操作。这两种方式提供的安全特性有所不同：

1. 在明文上生成MAC (MAC-then-Encrypt or Encrypt-and-MAC are more common than just MAC on plaintext if confidentiality is also needed, but let’s stick to the question’s phrasing):

   • 操作： 先计算明文的MAC，然后将明文和MAC一起发送（如果需要机密性，则再对明文和MAC一起加密，或者先加密明文，再对明文和密文的MAC进行处理，但这里按问题字面理解为只对明文做MAC）。
   • 提供的安全特性：
     • 认证 (Authentication)： 是的，接收方可以验证消息来源。
     • 完整性 (Integrity)： 是的，接收方可以验证明文内容未被篡改。
     • 机密性 (Confidentiality)： 不提供。 因为消息本身是以明文形式存在的（或者即使MAC本身被加密，明文也可能未加密）。如果攻击者能看到传输的数据，它就能看到明文内容。

2. 在加密消息上生成MAC (Encrypt-then-MAC 模式，这是推荐的做法)：

   • 操作：
     1. 先用一个密钥 $k_{enc}$ 对明文进行加密，得到密文。
     2. 然后用另一个密钥 $k_{mac}$ （或者从 $k_{enc}$派生出的密钥）对这个密文计算MAC。
     3. 将密文和这个基于密文的MAC一起发送。
   • 提供的安全特性：
     • 认证 (Authentication)： 是的，接收方可以验证密文的来源（间接验证了明文来源，因为只有合法方能正确加密并生成MAC）。
     • 完整性 (Integrity)： 是的，接收方可以验证密文未被篡改。如果密文被篡改，MAC校验会失败。这也间接保护了明文的完整性，因为如果密文未变，解密出的明文也不会变。
     • 机密性 (Confidentiality)： 是的，因为消息本身是以密文形式传输的。

   为什么Encrypt-then-MAC更好？
   这种模式被广泛认为是更安全的组合方式。如果先MAC再加密（MAC-then-Encrypt），攻击者可能在不知道加密密钥的情况下，对密文进行某些操作（比如重放部分密文块）而MAC仍然有效，或者从MAC中泄露关于明文的信息。而Encrypt-then-MAC模式下，MAC是针对最终要传输的密文计算的，任何对密文的篡改都会导致MAC验证失败，从而被接收方发现。接收方会先验证MAC，如果MAC有效，再进行解密。

速记： MAC+明文 = 认证+完整性（但无机密性）；（推荐）先加密再对密文MAC (Encrypt-then-MAC) = 认证+完整性+机密性。

总结：串联起来的安全图景

我们从网络安全的三个基本目标（机密性、完整性、认证）出发，了解了它们对于保护我们数字生活的重要性。

接着，我们深入探讨了对称密钥加密，它使用单一共享密钥进行高效的加解密，但面临密钥分发的难题。

为了解决密钥分发，我们引入了公钥密码体制（非对称加密），它利用数学难题（如大整数分解、离散对数）来保证公钥公开而私钥安全。在HTTPS等实际应用中，非对称加密被巧妙地用来安全交换对称加密所需的会话密钥，之后再用高效的对称加密进行大规模数据传输。

最后，我们讨论了如何确保消息的真实来源和内容未被篡改。我们否定了使用易被伪造的物理MAC地址进行验证的方法，转而学习了基于哈希函数的消息认证码 (HMAC)。HMAC通过共享密钥和哈希运算为消息生成一个“指纹”，有效提供认证和完整性。我们还比较了在明文上和在密文上生成MAC的差异，强调了“先加密后认证（Encrypt-then-MAC）”模式的安全性优势，它可以同时提供机密性、完整性和认证。

希望通过这趟旅程，你对网络安全的核心概念有了更清晰的认识。网络安全是一个不断发展、攻防双方持续博弈的领域，但理解了这些基础原理，你就拥有了探索更广阔安全世界的钥匙。

---

习题与答案

为了巩固今天学习的内容，这里有几道练习题，请尝试回答：

1. 问题1： 请简述网络安全中“CIA三元组”通常指的是哪三个特性？并简要解释每个特性的含义。
2. 问题2： 对称密钥加密最主要的优点是什么？它最根本的挑战又是什么？
3. 问题3： 在HTTPS通信中，浏览器是如何安全地将用于对称加密的会话密钥传递给服务器的？这个过程中利用了什么类型的加密技术？
4. 问题4： 为什么说仅使用网络设备的MAC地址来验证数据来源是不可靠的？HMAC是如何解决这个问题的？
5. 问题5： 如果一个系统需要同时保证消息的机密性、完整性和来源认证，那么在消息加密和生成MAC码的顺序上，通常推荐哪种做法？为什么？

---

答案：

1. 答案1：

   • CIA三元组通常指：
     • 机密性 (Confidentiality)： 确保信息不被泄露给未经授权的访问者。
     • 完整性 (Integrity)： 确保信息在存储或传输过程中保持准确和未被篡改。
     • 可用性 (Availability)： 确保授权用户在需要时可以访问信息和相关资源。（虽然本次博客重点是C、I和Authentication，但CIA三元组标准定义包含Availability）。
   • 根据题目提供的上下文，如果特指本博客内容，也可以回答：
     • 机密性 (Confidentiality)： 确保信息不被泄露给未经授权的个人、实体或进程。
     • 完整性 (Integrity)： 在数据的整个生命周期中，保持其一致性、准确性和可信度，防止未经授权的篡改。
     • 认证 (Authentication)： 验证用户、进程或设备的身份，以授予对资源的访问权限。

2. 答案2：

   • 主要优点： 加密和解密速度快，计算开销小，适合对大量数据进行加密。
   • 根本挑战： 密钥分发问题。即如何在不安全的信道上，让通信双方安全地共享那个唯一的对称密钥。

3. 答案3：

   • 在HTTPS中，浏览器首先从服务器获取其数字证书，证书中包含服务器的公钥。浏览器生成一个随机的会话密钥（用于对称加密），然后使用服务器的公钥对这个会话密钥进行加密。加密后的会话密钥被发送给服务器，服务器使用其对应的私钥进行解密，从而获得会话密钥。
   • 这个过程利用了**非对称加密（公钥加密）**技术来安全地协商和传递对称加密所需的会话密钥。

4. 答案4：

   • 仅使用网络设备的MAC地址不可靠，因为MAC地址可以被轻易地伪造（欺骗）。攻击者可以配置自己的设备使用与合法设备相同的MAC地址，从而冒充合法设备。
   • HMAC通过以下方式解决问题：它要求通信双方共享一个秘密密钥。HMAC的计算结果（MAC码）同时依赖于消息内容和这个共享密钥。不知道密钥的攻击者即使截获或篡改了消息，也无法计算出正确的MAC码。接收方通过验证MAC码，既能确认消息来源（因为只有密钥持有者能生成正确的MAC），也能确认消息的完整性（因为消息任何改动都会导致MAC不匹配）。

5. 答案5：

   • 通常推荐的做法是 “先加密，后认证”（Encrypt-then-MAC）。
   • 原因： 这种模式下，首先对明文进行加密得到密文，然后对这个密文计算MAC码。
     • 机密性： 通过加密明文实现。
     • 完整性与认证： MAC码是针对密文生成的。接收方首先验证密文的MAC。如果MAC无效，说明密文在传输中被篡改或来源可疑，可以直接丢弃，避免了解密可能被篡改的（甚至恶意的）密文所带来的风险。如果MAC有效，再进行解密。这种方式能更好地防止针对密文的某些攻击（如padding oracle attack），并确保认证的是最终传输的密文数据。