当前位置：首页 > news >正文

three.js+WebGL踩坑经验合集(8.2):z-fighting叠面问题和camera.near的坑爹关系

news 来源：原创 2025/5/19 0:11:10

本篇延续上篇内容：

three.js+WebGL踩坑经验合集(8.1):用于解决z-fighting叠面问题的polygonOffset远没我们想象中那么简单-CSDN博客

笔者在上篇提到，叠面的效果除了受polygonOffset影响以外，还跟相机的近裁剪面camera.near密切相关，之所以要把near参数放到前面来讲，原因是，camera.near在绝对值很小的时候，哪怕不是个叠面，也会有很奇葩的现象。

这里，笔者在上一篇demo的基础上做一些调整，让两个面相互垂直。

<!DOCTYPE html>
<html lang="en">

<head>
  <meta charset="UTF-8">
  <title>叠面测试</title>
  <style>
    body {
      margin: 0;
      overflow: hidden;
      /* 隐藏body窗口区域滚动条 */
    }
  </style>
  <!--引入three.js三维引擎-->
  <script src="three/build/three.js"></script>
  <script src="three/examples/js/controls/OrbitControls.js"></script>
  <script src="three/examples/js/libs/dat.gui.min.js"></script>

</head>

<body>
  <script>
    /**
     * 创建场景对象Scene
     */
    var scene = new THREE.Scene();

    /**
     * 创建网格模型
     */
    var geometry = new THREE.PlaneGeometry(100, 100);
    var material = new THREE.MeshBasicMaterial({
      color: 0xFF6600,
      side: THREE.DoubleSide,
      polygonOffset: true,
      polygonOffsetFactor: 0,
      polygonOffsetUnits: 0

    });
    var mesh = new THREE.Mesh(geometry, material);
    scene.add(mesh);

    var geometry2 = new THREE.PlaneGeometry(50, 50);
    var material2 = new THREE.MeshBasicMaterial({
      color: 0xFFFFFF,
      side: THREE.DoubleSide,

    }); //材质对象Material
    var mesh2 = new THREE.Mesh(geometry2, material2);
    mesh2.rotation.y = Math.PI * 0.5;
    scene.add(mesh2);

    /**
     * 相机设置
     */
    var width = window.innerWidth;
    var height = window.innerHeight;
    var k = width / height;
    //创建相机对象
    var camera = new THREE.PerspectiveCamera(60, k, 0.01, 2000);
    camera.position.set(0, 0, 200);

    /**
     * 创建渲染器对象
     */
    var renderer = new THREE.WebGLRenderer();
    renderer.setSize(width, height);//设置渲染区域尺寸
    renderer.setClearColor(0x000000, 1); //设置背景颜色
    document.body.appendChild(renderer.domElement); //body元素中插入canvas对象
    //执行渲染操作   指定场景、相机作为参数
    function render() {
      renderer.render(scene, camera);//执行渲染操作
    }
    render();
    var controls = new THREE.OrbitControls(camera, renderer.domElement);//创建控件对象
    controls.addEventListener('change', render);//监听鼠标、键盘事件
    //间隔20ms周期性调用函数fun,20ms也就是刷新频率是50FPS(1s/20ms)，每秒渲染50次
    setInterval("render()", 20);

    var gui = new dat.GUI();
    var camFolder = gui.addFolder("相机");
    propsCamera = {
      get '裁剪'() {
        return camera.near;
      },
      set '裁剪'(v) {
        camera.near = v;
        camera.updateProjectionMatrix();
      },
    };
    gui.add(propsCamera, "裁剪", 0.001, 0.01);

    var offsetFolder = gui.addFolder("polygonOffset");
    propsOffset = {
      get 'polygonOffsetFactor'() {
        return material.polygonOffsetFactor;
      },
      set 'polygonOffsetFactor'(v) {
        material.polygonOffsetFactor = v;
      },

      get 'polygonOffsetUnits'() {
        return material.polygonOffsetUnits;
      },
      set 'polygonOffsetUnits'(v) {
        material.polygonOffsetUnits = v;
      },
    };
    gui.add(propsOffset, "polygonOffsetFactor", 0, 10);
    gui.add(propsOffset, "polygonOffsetUnits", 0, 10);

  </script>
</body>

</html>

运行效果如下图所示。

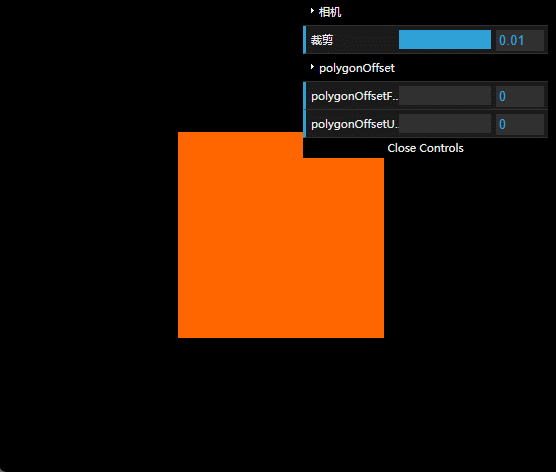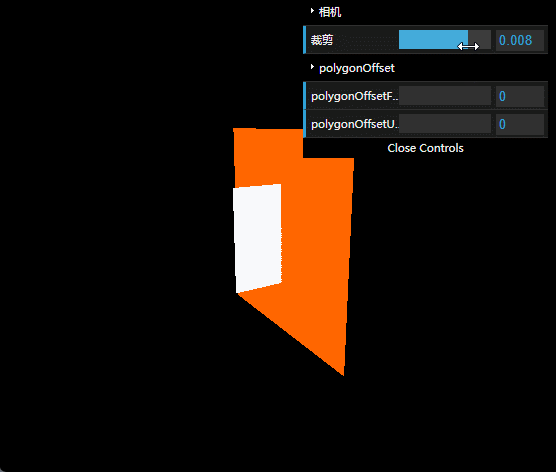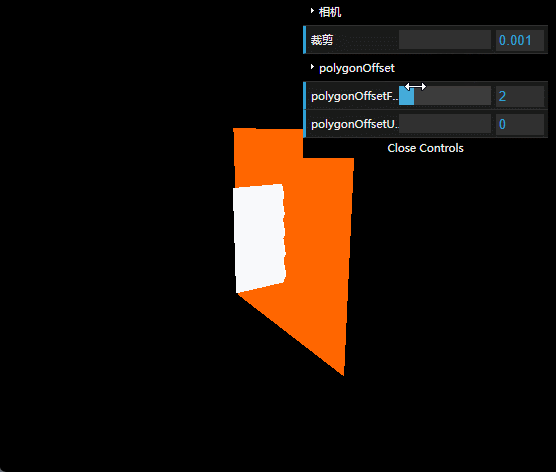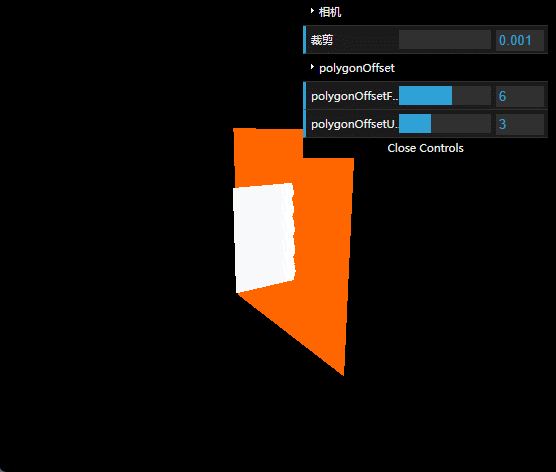
可以看到，当我们把camera的near调小时，两个面的交线从直线变成波浪线。这个时候，你去调整polygonOffset就会有一种波浪翻滚的效果。虽然有点意思，但往往都不是我们需要的。

裁剪从业务功能上理解，就是用于调整z方向可视化区域的范围，按道理它不应该影响可视区域内的元素的显示效果，但现在我们发现了坑。而且不难想象，在这种情况下，调叠面也是很容易踩雷的。

因此，如果没有什么特别的要求，camera的near不建议调很小的绝对值，更不要弄成负数，至于为什么，这要从投影矩阵的公式说起。

如前面的文章所言，笔者对网上那些透视投影矩阵公式推导的文章相当满意，所以不打算再造轮子，而仅仅是把现有公式抄过来进行研究。

其中n=camera.near，f=camera.far

笔者之前写过的文章里提到，最终呈现到屏幕上用的z值=z/w

three.js+WebGL踩坑经验合集(4.2):为什么不在可视范围内的3D点投影到2D的结果这么不可靠-CSDN博客

所以我们拿矩阵的第3和第4行进行计算即可。

投影前的z记为Z，投影后记为z，w投影前恒定为1。

根据投影矩阵公式（不了解矩阵运算的可以自行查阅相关资料，也可以找笔者前面写的《矩阵的史诗级玩法》专栏进行学习），我们有

z = 0*x+0*y+Z(n+f)/(n-f)+2fn/(n-f)=Z(n+f)/(n-f)+2fn/(n-f)

w = 0*x+0*y+Z*(-1)+0=-Z

最终结果depth=z/w=(Z(n+f)/(n-f)+2fn/(n-f))/(-Z)

=-(n+f)/(n-f)-2fn/(n-f)/Z

可以看到，投影结果需要除以投影前的Z值，因此，投影前后的关系式为非线性，它是一个反比例曲线。

为了让大家可以更直观地看到这条曲线，笔者做了个demo给大家进行演示（demo代码不给出，因为用excel等工具也能做，用代码写只为演示方便，实在想要的可以评论留言跟我拿）

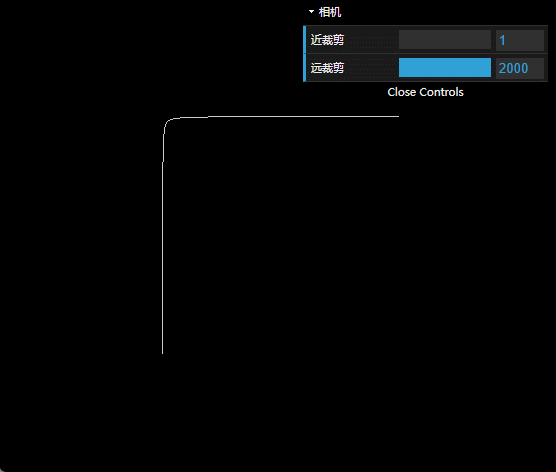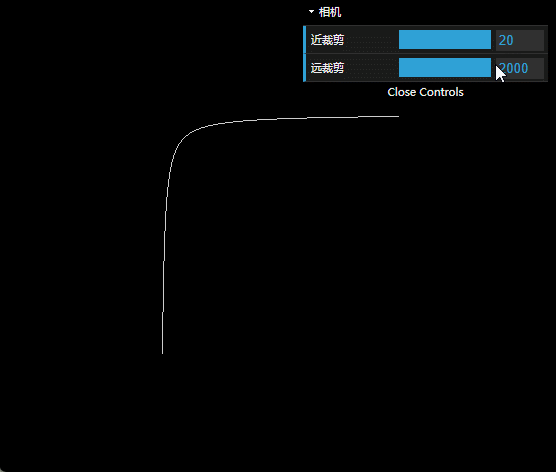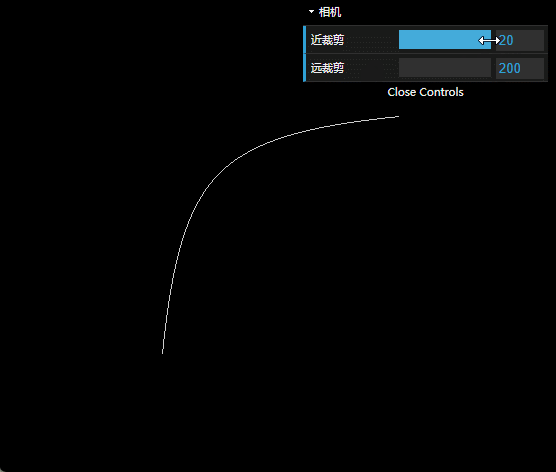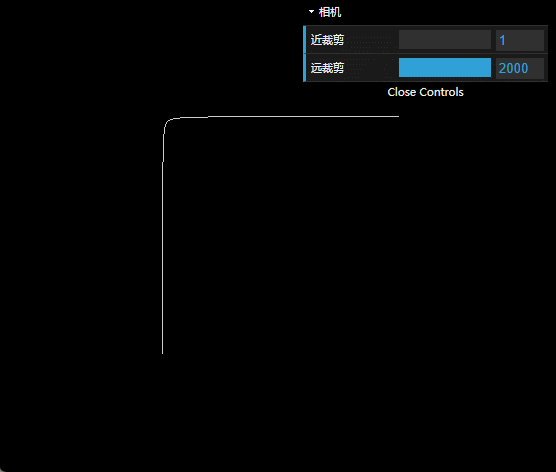
图上，横坐标代表z坐标，纵坐标代表深度值。

大家会发现，近裁剪面调大，远裁剪面调小，曲线都会变得平缓，没开始时那么陡峭。

曲线很陡峭的时候，深度的整个值域就会被很小的一个z区间占据，比如z=1的时候，1到2占据了深度超过99%的区间，剩下的2跟2000就只能分到1%的深度范围，导致深度值从2变到2000的过程里面没法拉开，因此就出现了前面给出来的，两个面的交线产生波浪的效果。

笔者观察发现，曲线的形状跟far和near的比值相关，比如2和200跟20和2000出来的形状一样。

下面我们来验证一下，设f/n=p，则f=np，代入到上面给的depth公式中，得到

不难发现，函数的图像就跟p=f/n有关。

所以，想要解决叠面问题（解决？这是不可能的，只能缓解），我们要做的其中一件事情，是让相机矩阵的far和near的比值尽可能地小。但是far值通常比较大，调小的话很容易就会把业务功能改坏，把2000改到200，场景都被切没了，产品和测试不得马上找你算账？所以，不管是我们CTO给的方案，还是笔者的标题，都没有提及far参数，尽管它的确也跟叠面问题有关系。然而，把near从0.001变成1，那不但功能上没有太大影响（至少笔者接触到的业务场景是这样），而且叠面问题可以得到非常有效的缓解，因为这一下，far/near的值可以马上下降几个数量级。

最后还要提一嘴，以上的坑只出现在透视相机，正交相机不存在，或者说就算有也远没有透视的那么大。因为透视相机下，w恒等于1，z/w是个直线的一次函数，而非可能很陡峭的反比例函数，有兴趣的读者可以自行演算正交相机的深度公式，此处就不展开了。

下面笔者来小结一下：

1 在透视相机中，far/near较大时，z-fighting叠面问题会比较严重，调polygonOffset适应不同角度的难度会增大

2 如果透视相机的far/near非常大，那么z-fighting甚至会影响到两个垂直面的交线，直线也会变波浪

3 使用透视相机时，应根据业务场景的实际情况，让far/near的值更加小，如果允许near设置为10，那么叠面问题会更好缓解

4 正交相机不用过多考虑far/near的值，但也不宜弄太大，毕竟near太小容易出现精度问题

后面笔者继续跟大家讨论polygonOffset的时候，会在一个far/near比较合理的范围内进行，否则垂直面的交线都打架了还玩个毛线，对吧。

不难想象，调整polygonOffset的时候，对于相机可以在幅度较大的变化项目而言，我们设置的时候，还得至少考虑上near和far，写死的魔术数总会不太可控。

嗯好了，本篇就到此结束，下篇我们将试着深入研究polygonOffset这个坑爹玩意，等笔者的好消息。