排序--计数排序
一,引言
计数排序是一种针对整数数据的高效排序算法。其主要流程可分为三个步骤:首先计算整数数据的数值范围;接着按大小顺序统计各数值的出现次数;最后根据统计结果输出排序后的数据序列。
二,求最值
遍历现有数据,获取最大值和最小值。通过计算两者差值确定数据区间范围,据此确定统计次数数组的分配空间大小。举个例子:

经过遍历得到最小值为1,最大值为9。用最大值减去最小值再加1,可得出数据范围为1到9,共包含9个不同数值。因此需要分配能存储9个整型数据的空间。代码如下:
void sort(int* arr, int n)
{int min = arr[0];int max = arr[0];for (int i = 1; i < n; i++){if (arr[i] < min){min = arr[i];}if (arr[i] > max){max = arr[i];}}int* p = (int*)calloc((max - min + 1), sizeof(int));
}三,统计次数
遍历原数组时,先用最小值调整每个元素,将其转换为计数数组的索引位置。随后在计数数组对应的索引位置进行累加操作。完成所有元素的遍历后,即可生成最终的计数数组。举个例子:
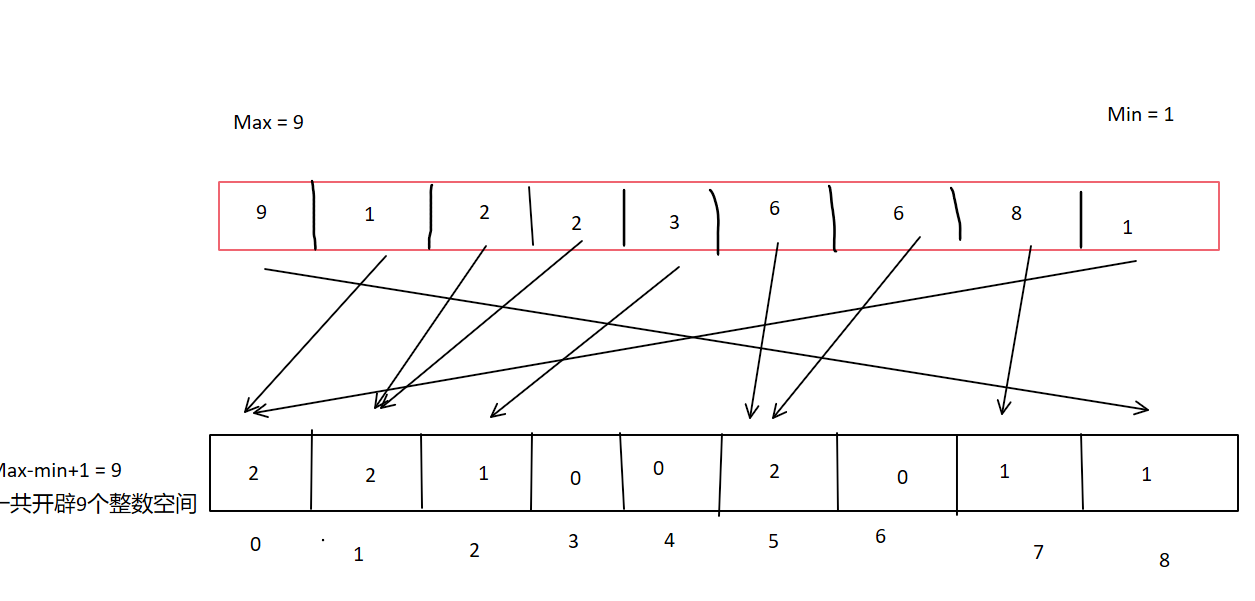
每一次箭头的指向代表进行一次加加操作。代码实现:
for (int i = 0; i < n; i++){p[a[i] - min]++;}四,排序
统计数组的每一个数据加上min就得出原数组的值。统计数组的顺序就是原数组排序后的相对位置。举个例子:

代码实现:
int j = 0;for (int i = 0; i < (max-min+1); i++){while (j[i]--){a[j++] = i + min;}}五,总结
计数排序的时间复杂度为ON远远小于一般排序,且该排序为稳定排序。但是计数排序要求输入数据必须是确定范围的整数。浮点数或字符串等数据类型无法直接使用该算法。当数据范围k远大于元素数量n时,需消耗O(k)额外空间存储计数数组。若k过大(如排序少量超大整数),会造成显著的空间浪费。对于动态范围或未知范围的数据,需先遍历确定范围值,增加预处理开销。此过程可能影响整体效率。
