深入理解坐标系的变换

在世界坐标系中对某个模型进行一个变换，旋转$R^{\ast }$，平移$t^{\ast }$。

已知模型坐标系中模型上所有点的坐标，以及世界坐标系中模型的位姿，求模型变换后所有点在世界坐标系中的位姿。

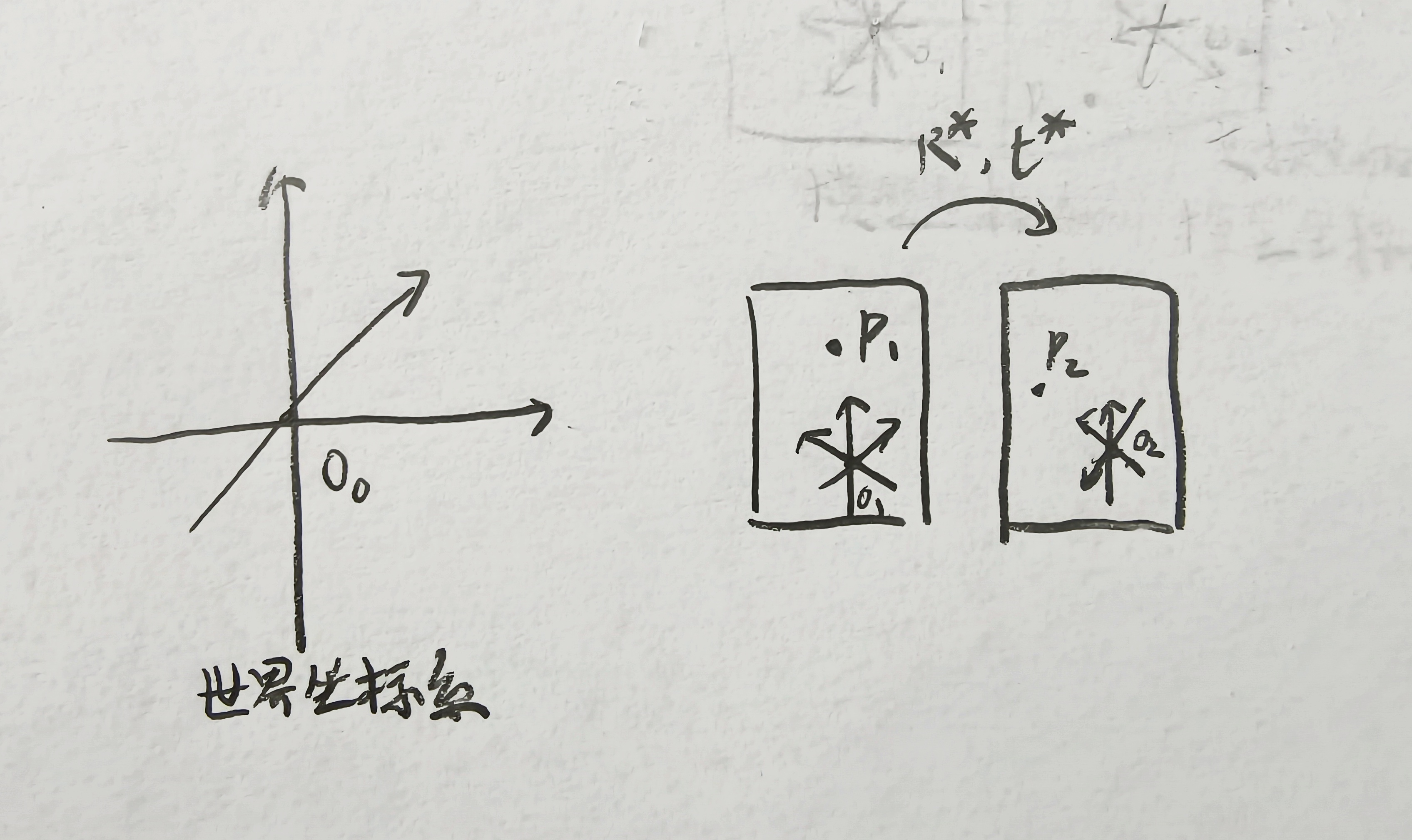
简化为符号语言：$p$代表模型中的任一点，$o$代表坐标系的原点，右上角标代表从哪个坐标系的视角来看。0、1、2分别代表世界坐标系、模型坐标系、变换过的模型坐标系。$p_1$是模型中的任一点，$p_2$是变换后的模型中与$p_1$对应的点，$o_0$是世界坐标系的原点，$o_1$是模型坐标系的原点，$o_2$是变化后的模型坐标系的原点。

举例：$p_1^0$代表世界坐标系下的$p_1$点的位置；$t^{\ast }=o_2^0-o_1^0$代表世界坐标系下从模型坐标系原点到变换后的模型坐标系原点的位移；

那么问题可以描述为，已知：
$$\begin{array}{rl}{p}_1^1& =p_2^2\\ p_1^0& =R_1^0\cdot p_1^1+o_1^0\\ p_2^0& =R_2^0\cdot p_2^2+o_2^0\\ p_2^0-o_2^0& =R^{\ast }\cdot (p_1^0-o_1^0)\\ t^{\ast }& =o_2^0-o_1^0\end{array}$$
$1$：因为$p_2$是变换后的模型中与$p_1$对应的点

$2,3$：坐标变换的基本原理

$4,5$：在世界坐标系中对模型进行变换的原理

那么为了求$p_2^0$，从上式可知，$R^{\ast }=R_2^0(R_1^0{)}^{-1}$，进而$p_2^0=R^{\ast }\cdot R_1^0\cdot p_1^1+o_1^0+t^{\ast }$，解毕。

这里的$R^{\ast }=R_2^0\cdot (R_1^0{)}^{-1}$以及$p_2^0-o_2^0=R^{\ast }\cdot (p_1^0-o_1^0)$揭示了施加变换旋转的原理：世界坐标系下的向量$(p_1^0-o_1^0)$通过$(R_1^0{)}^{-1}$进入到模型坐标系中，然后再施加$R_2^0$就能再次进入到世界坐标系中（由于模型坐标系中的p1和变换后的模型坐标系中的p2是对应的）。