7.2.1_顺序查找

知识总览：

顺序查找：

算法思想：

从头到脚挨个找或者从脚到头挨个找适用于线性表(顺序存储和链式存储都适用)，又叫线性查找

实现：

1个数组elem指向数组的起始位置，索引从0开始遍历数组直到找到目标值返回索引下标，否则返回-1

顺序查找-添加哨兵：

数组的第一个位置不存数据而是在查找的时候放目标值即哨兵，从索引1开始存放数据，然后从数组长度倒序查找比较目标值，如果找到目标值则返回索引下标，如果返回索引0证明没找到目标值，添加哨兵是为了避免数组越界，发现到了哨兵的位置就不再查找

 

查找效率分析： 

评价一个查找算法要看平均查找长度即ASL，平均查找长度又分查找成功和查找失败

假设找任何一个关键字的概率都是相同的，如果一共有n个关键字，假设找最后一个关键字则概率为1/n，如果找倒数第2个关键字，则需要对比2次，则找到的概率为2* 1/n，依次类推需要比较n次，则平均查找长度为(1+2+3+...+n)/n=(n+1)/2,查找失败为查找所有的数据都没有查找到，即比较了n+1次(有加1是因为哨兵还占了一个位置)，即查找成功和查找失败的时间复杂度都为O(n)

顺序查找的优化(对有序表)：

就是因为顺序查找是挨个找，所以假如要查找的数组数据开始有顺序的话就方便查找，视频中说得有n+1种失败的情况不知道从哪来的，可能是跟上边查找效率分析有关，把每次失败都加了区间范围，然后根据n+1种失败的情况再确定每次失败的概率为1/n+1，第2段要比较2次失败的概率为2*(1/n+1)。。。。。直到到如下数组中第n个数，因为n前后有2个范围段所以加了2次n，最后得到ASL=n/2+(n+1)/n

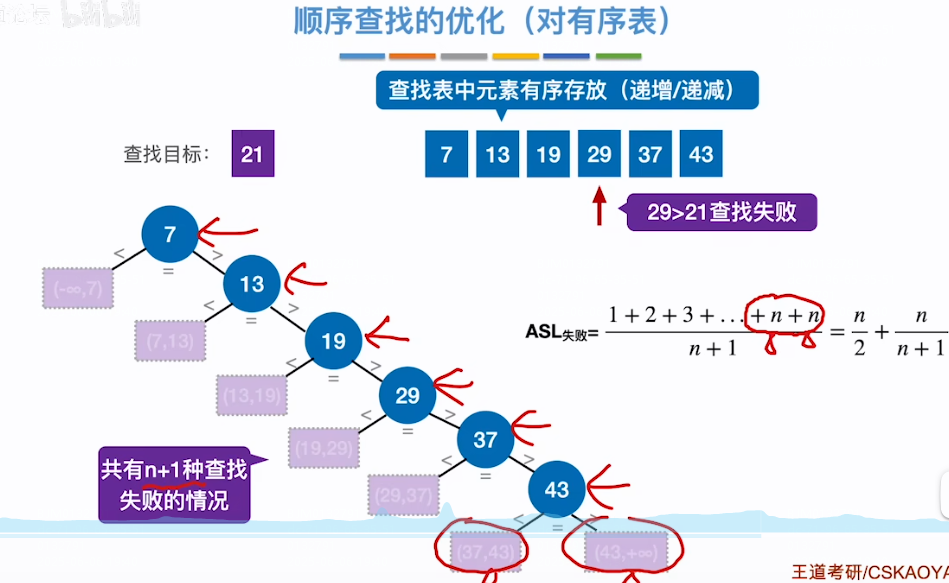
用查找判定树分析ASL：

方形节点为失败节点，圆形节点为成功节点， 如果要找的关键字在圆形节点即成功节点中，要付出的查找长度(关键字的对比次数)=自身所在的层数，比如要找关键字19，要进行7,13,19三次对比，失败节点的查找长度=父节点所在层数，假如关键字在13-19方形区间，直到确认失败需要对比7、13、19三次即父节点所在层数(就是圆形节点所在层数吗？)

顺序查找的优化(被查概率不相等)：

每个关键字的查找概率不相等，假如查找成功的概率大就把被查概率大的放前面有助于在查找成功时缩短ASL，但是此时数组的数据乱序，即可以提高查找成功的平均查找长度，但是查找失败的情况需要从头扫到尾才知道查找失败了，即查找失败的平均查找长度ASL非常大，故具体问题具体分析

不管怎么优化只要采用顺序查找，时间复杂度就是O(n)

 

知识回顾： 

听不懂在讲什么。。。。。。。。。