【Java算法】八大排序

八大排序算法

目录

注意：以下排序均属于内部排序

• （1）插入排序

  • 直接插入排序

  • 改进版本

    • 折半插入排序

    • 希尔排序

• （2）交换排序

  • 冒泡排序

  • 快速排序

• （3）选择排序

  • 简单选择排序

  • 堆排序（树形选择排序）

• （4）归并排序

• （5）基数排序

---

排序总结分析表

---

一、插入排序

1. 直接插入排序

（1）整体思路

通过动图可以形象的理解到

• 1. 抽出一张牌，和当前元素之前的元素逐个比较，如果比当前元素小，该元素就后移，直到找到插入位置

• 2. 在无序序列中抽取一张牌，通过比较插入到有序序列中

说明：（惯用思想）初始时视第一个元素是有序的，之后通过排序逐渐增大有序序列的长度

（2）代码实现

第一种写法：while 循环（更规范）

public static void insert_sort(int[] arr) {/*插入排序的思想：从无序的序列中拿一个数，通过比较的方式插入到有序序列中初始状态：假设第一个数是有序的，从第二个元素开始，和有序序列比较，然后插入*/// 在无序序列中抽取一张牌for (int i = 1; i < arr.length; i++) {// 记录要插入的元素值，位置位于有序序列的末尾int insertvalue = arr[i];// 在有序序列中从后往前和插入元素比较，找到插入位置int j = i - 1;/*1 2 3 9 10 15 5插入5：需要插入在3的后面。所以只要插入元素比当前比较元素小，就往后移*/// 推荐这种写法，更规范while (j >= 0 && insertvalue < arr[j]) {arr[j + 1] = arr[j]; //  元素后裔j--;}// 插入元素（插入到  比当前插入元素小的 元素  的后面）arr[j + 1] = insertvalue;}
}

第二种写法：使用for 循环

public static void insert_sort_1(int[] arr) {// 第二种写法：使用for循环for (int i = 1; i < arr.length; i++) {int insertvalue = arr[i];int j = i - 1;for (; j >= 0; j--) {if (insertvalue < arr[j]) {arr[j + 1] = arr[j];}else{break; // 如果 insertvalue >= arr[j] 就退出循环}}arr[j + 1] = insertvalue;}
}

---

2. 折半插入排序

改进点：使用折半查找提高效率，使用循环遍历逐个匹配的效率太差

    // 查找插入位置的方法采用二分思想（由于查找位置的序列本身就是有序的，所以可以使用二分）
public static void binary_insert_sort(int[] arr) {for (int i = 1; i < arr.length; i++) {// 初始时：把第一个元素看成是有序的，然后进行插入排序int insertvalue = arr[i];int left = 0;int right = i - 1; // 和 j = i -1 是等价的while (left <= right) {int mid = left + ((right - left) / 2);if (arr[mid] < insertvalue) {left = mid + 1;} else {right = mid - 1;}}// 找到了插入位置，移动元素为插入做准备// 为了维持稳定性，应该插入到 right 的后边// 插入位置为 right + 1 , 需要把这个位置空出来才可以插入，所以要取等for (int j = i - 1; j >= right + 1; j--) {arr[j + 1] = arr[j]; //元素后移}arr[right + 1] = insertvalue;}
}

---

3. 希尔排序

动图演示

使用间隔 gap，gap 逐渐递减，最后 gap 的值必须是一，每一轮排序对 gap 产生的序列进行排序

快速写希尔排序：把直接插入排序中 “ 1 ” 的位置全部替换成 “ gap ”

/*
快速写希尔排序算法代码：只要把直接插入排序中为 1 的地方全部改成 gap 即可*/
public static void shell_sort(int[] arr){// 增量序列取中间值（常用方法）/*增量序列是递减的，并且最后一个值一定是一*/int gap = arr.length / 2; // 向下取整while (gap >= 1) {shell(arr, gap);gap /= 2;}
}// 一趟写入排序的过程
public static void shell(int[] arr, int gap){// 思想和直接插入排序，不同点就在原来 “加/减一” 的位置全部变成 “gap”// 由于是分组排，这里需要包含分组的第一个元素，所以不加一for (int i = gap; i < arr.length; i++) {int insertvalue = arr[i];int j = i - gap;// 移动元素while(j >= 0 && insertvalue < arr[j]){arr[j + gap] = arr[j];j -= gap;}arr[j + gap] = insertvalue;}
}

---

二、交换排序

1. 冒泡排序

动图演示

（1）普通版本

public static void bubble_sort(int[] arr){for (int i = 0; i < arr.length - 1; i++) {for (int j = 0; j < arr.length - 1 - i; j++) {// 前面的比后面大，交换位置if(arr[j] > arr[j + 1]){int temp = arr[j];arr[j] = arr[j + 1];arr[j + 1] = temp;}}}
}

（2）改进版本

亮点：通过变量标记的方式标记是否执行了交换操作，可以一定程度上减少比较次数

// 改进版本：如果本身就有序，则无序交换，减少比较次数
public static void bubble_sort_improve(int[] arr){for (int i = 0; i < arr.length - 1; i++) {int flag = 0;  // 每次进入循环都标记为0，如果有序就不交换，flag = 0for (int j = 0; j < arr.length - 1 - i; j++) {// 前面的比后面大，交换位置if(arr[j] > arr[j + 1]){flag = 1; // 交换了就标记为一int temp = arr[j];arr[j] = arr[j + 1];arr[j + 1] = temp;}}if(flag == 0){/* 在一趟遍历之后，如果都没有发生交换，说明元素已经有序了，后面的比较没有意义了，直接退出*/break;}}
}

---

2. 快速排序

动图演示

主要思想：递归，双指针（对撞指针）

思路分析

• 把第一个元素当作枢纽，然后通过两个指针 left 和 right

• left ： 在前面找比枢纽大的元素搬到枢纽的后面

• right ： 在后面找比枢纽小的元素搬到枢纽的前面

• 递归左右子区间

 /*快速排序是冒泡排序的改进版本，核心在于递归和双指针思想说明1.选取数组的第一个元素为枢纽2.left,right为数组下标3.延申：可以对任意区间排序*/public static int partition(int[] arr, int left, int right) {/*双指针思想1.left：指向数组的 第一个 元素，从 左往右 找，如果比中间值 大，就搬到后面（high的位置）2.right：指向数组的 最后一个 元素，从 左右往左 找，如果比中间值 小，就搬到前面（left的位置）*/int pivot = arr[left];// 两个指针的移动逐渐靠近，当两个指针重合时，退出循环// 此时指向的位置就是枢纽的位置while (left < right) {/*注意：指针的移动可能会越界，需要加上判断条件 left < right易错点：先找小的，后找大的*/// 首先在后面找小的往前搬(那对立面就是不符合要求，right指针往前移)while (arr[right] >= pivot && left < right) {right--;}arr[left] = arr[right];// 然后在前面找大的往后搬(那对立面就是不符合要求，left指针往后移)while (arr[left] <= pivot && left < right) {left++;}arr[right] = arr[left];}// 此时 left = right，指向中间枢纽的位置，放入枢纽值，返回枢纽的位置arr[left] = pivot;return left;
}public static void quicksort(int[] arr, int left, int right) {/*递归易错的地方：需要有一个递归出口*/if(left < right){int pivot = partition(arr,left,right); // 首先计算枢纽值// 递归递归左子区间quicksort(arr,left,pivot - 1);// 递归排序右子区间quicksort(arr,pivot + 1,right);}
}

---

三、选择排序

1. 简单选择排序

动图演示

基本思路：选一个数，在这个数的后面找有没有比本身还小的，有就交换位置

优化点：在后面找一个最小的数，避免重复的覆盖，减少比较次数

区别冒泡排序的优化

• 冒泡排序中是比较相邻两个元素之间是否有序，如果有序就不交换位置

• 选择排序中是在后面找一个比本身小的数，然后交换位置，为了避免重复的覆盖，需要找到一个最小的数进行交换

（1）普通版本

public static void select_sort(int[] arr){for (int i = 0; i < arr.length; i++) {for (int j = i + 1; j < arr.length; j++){if(arr[j] < arr[i]){int temp = arr[j];arr[j] = arr[i];arr[i] = temp;}}}
}

（2）改进版本

public static void select_sort_improve(int[] arr){// 比较 n-1 趟for (int i = 0; i < arr.length; i++) {int min_index = i; // 假设当前元素是最小的，记录下标// 在当前元素的后面找有没有更小的，有就交换位置for (int j = i + 1; j < arr.length; j++){// 如果找到更小的，就更新下标if(arr[j] < arr[min_index]){min_index = j;}}// 如果最小元素不是本身（找到了更小的），就交换位置if(min_index != i){int temp = arr[i];arr[i] = arr[min_index];arr[min_index] = temp;}}
}

2. 堆排序（二叉堆）

（1）基本介绍

• 堆的性质是符合完全二叉树的，在结构上是递归定义的树结构

• 重要性质回顾

  • 1. 若一个非叶子节点节点的物理位置为 “ i ”

    • （1）左孩子

      • 物理位置：“ 2i ”

      • 数组下标：“ 2i + 1 ”

    • （2）右孩子

      • 物理位置：“ 2i + 1 ”

      • 数组下标：“ 2i + 2 ”

  • 2. 若一个数组的元素可以构成一棵树，数组大小为 n

    • （1）最后一个元素（叶子节点）在树中的标号对应的数组下标是n / 2

    • （2）从后往前遍历的第一个非叶子节点在树中的标号对应的数组下标是[n / 2] - 1

补充：关于树中节点的序号和数组下标的关系

方法：从左到右，从上到下依次标号

图例（对应数组下标）

       0/   \1      2/ \    / \3   4  5   6

• 分类

  • 大根堆：对于完全二叉树中的任意一个节点，其值都大于或等于其子树中所有节点的值。这意味着大根堆的根节点是堆中最大的元素

  • 小根堆：完全二叉树中任意一个节点的值都小于或等于其子树中所有节点的值，即小根堆的根节点是堆中最小的元素

大根堆示例

       10/    \8      6/ \    / \5   3  2

小根堆示例

       1/    \3      4/ \    / \6   8  9

（2）堆排序思想

• 1. 构建一个大根堆

  • 从后面的=第一个非叶子节点（下标：n / 2 - 1）开始，依次递归的往上调整，使得整棵树形成大根堆的结构

• 2. 交换最大和最小的节点，重新调整堆

  • 交换思想：交换的过程就是排序的过程，把最大的和最小的交换，即把最大的放入有序区，数组从后往前依次递减排序

  • 调整堆思想：先调整一颗树的左右孩子和根节点的大小关系，构成大根堆后，采用递归思想，递归调整左右子树

    • 理解：在调整过程中，指向的最大根节点会发生变化，对根节点调整即可实现对左右子树的调整）

• 3. 重复 2 的操作（ n 个元素进行 n - 1 趟排序）

  • 关于n - 1的说明

    • （1）进行n - 1 趟排序

    • （2）循环的起始变量，对应数组中最后的那个元素，刚好可以和第一个元素完成交换操作（最大的和最小的交换）

    • （3）循环过程中，刚好对应堆的大小的变化，每一轮排序一个元素（交换的过程），堆中需要调整的元素总数减小一

堆排序代码

/*
堆排序思想（又叫二叉堆）
分类：大顶堆，小顶堆堆符合二叉树的性质说明：数组的下标在树中是：从上到下，从左到右依次编号的排序过程说明1. 构建一个大顶堆，每次交换最小和最大的，并且堆大小缩小减一，
2. 交换的过程：把最大的放在有序区，但是破坏了大顶堆的结构，需要重新调整堆3. 有序的过程：把最大的放在有序区，数组从后往前一次放入有序元素完成排序*/// 堆调整（大顶堆）
// n：表示数组的大小；i：表示最大值的下标索引
public static void heapify(int[] arr, int n, int i) {/*易错：这里表示的下标值，然而二叉树中的性质指的是物理位置数组是从0开始编号的，举例说明7/   \6     57：下标索引是06：按照物理位置计算方法（左孩子：2 * i = 0），结果还是0，但是下标索引是1得出的关系：在物理位置的基础上加一才是索引下标*/int max_index = i; // 初始化最大值下标索引int left = 2 * i + 1; // 左孩子的下标索引int right = 2 * i + 2; // 右孩子的下标索引// 和左右孩子比较，更新最大值下标索引// 注意：防止越界，需要加上限制条件if (left < n && arr[left] > arr[max_index]) {max_index = left;}if (right < n && arr[right] > arr[max_index]) {max_index = right;}// 如果最大值不是初始化的值，说明找到了更大的值，把最大值放到根节点if (max_index != i) {int temp = arr[i];arr[i] = arr[max_index];arr[max_index] = temp;// 递归调整左右子树（max_index在这个过程中做了更新）heapify(arr, n, max_index);}
}//堆排序
public static void heap_sort(int[] arr) {/*7/   \6     5/ \   / \4   3 2   1总节点数：7循环起点：7/2 - 1 = 3 - 1 = 2，即下标为2的元素开始（元素5）*/// 构建大顶堆（如果每一个子树都是大顶堆，则整个二叉堆就是大顶堆）int n = arr.length;// 从最后一个非叶子节点开始向上进行堆调整for (int i = n / 2 - 1; i >= 0; i--) {heapify(arr, n, i);}// 排序过程：交换元素，调整堆，进行 n - 1 趟排序// 初值：每交换一次，可以理解为排序一个元素，则堆中需要排序的元素总数减少一// 初值为 i -1 正好对应最后一个元素的下标，方便交换for (int i = n - 1; i > 0; i--) {// 把最大的和最小的进行交换int temp = arr[0];arr[0] = arr[i];arr[i] = temp;// 交换后破坏了大顶堆的结构，重新调整堆（排序的过程中堆的大小在递减）heapify(arr, i, 0);}
}

---

四、归并排序

动图演示

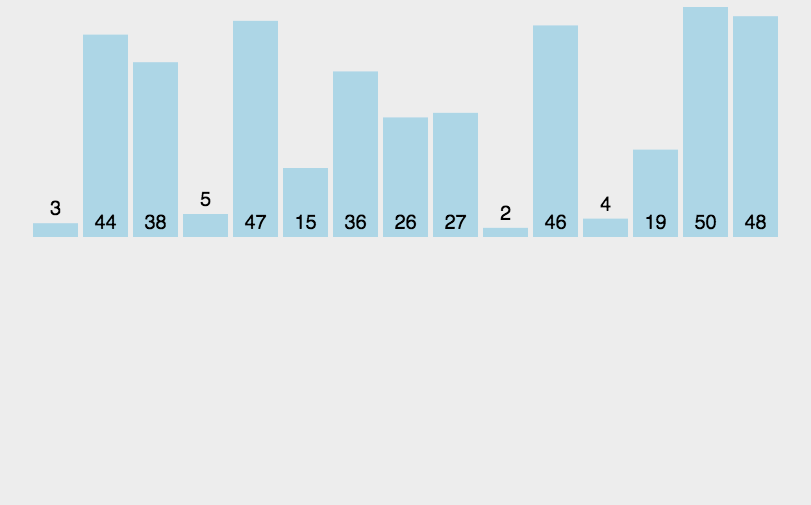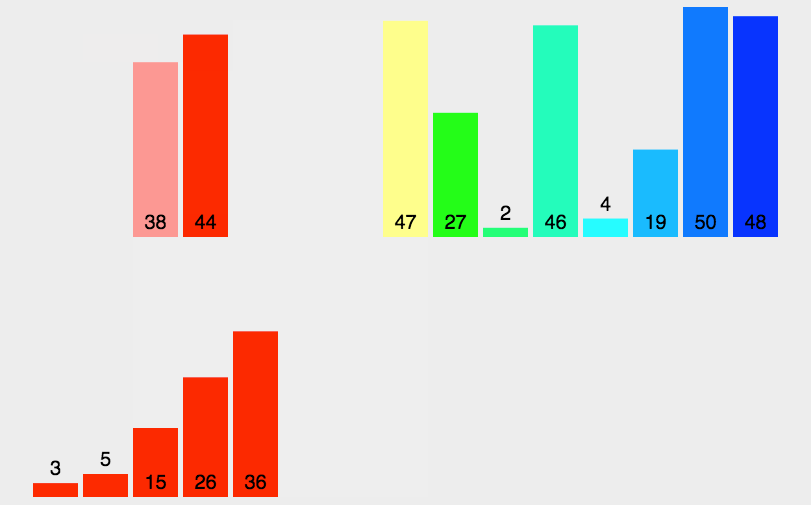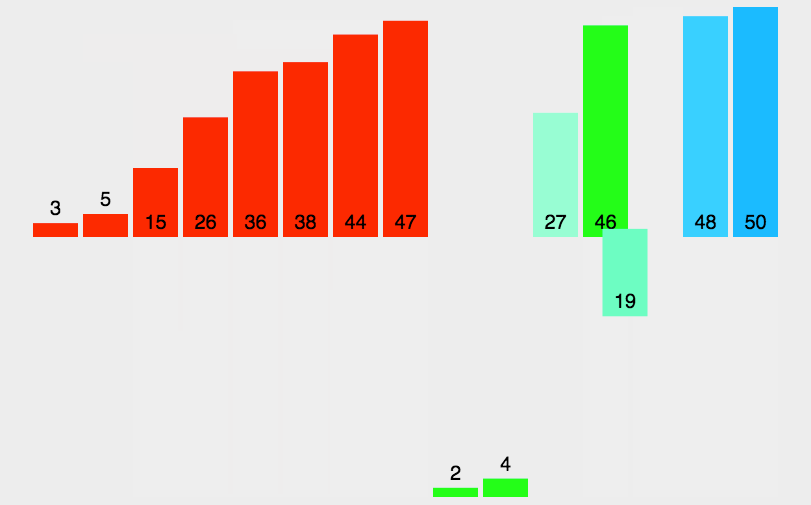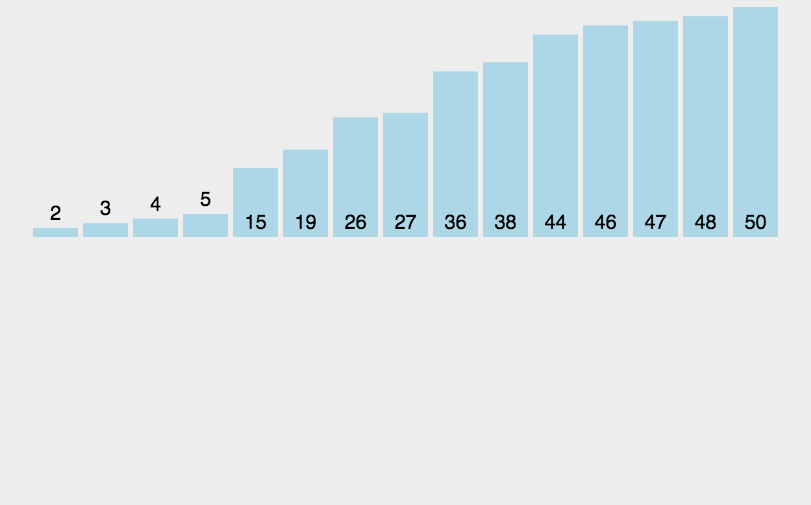
思路：运用合并为有序序列的思想、递归思想，两个有序序列通过比较的方式合并成一个更长的有序序列，而比较的过程正好是排序的过程

小结：排序左区间，排序右区间，两个区间合并，然而排序的过程又是两个区间合并的过程，即采用递归思想

归并排序代码

---

五、基数排序