当前位置：首页 > news >正文

2025年大一ACM训练-尺取

news 来源：原创 2025/6/1 11:52:42

2025年大一ACM训练-尺取

尺取法（Sliding Window）：

1. 基本概念
尺取法（又称滑动窗口法）是一种通过维护窗口的左右边界来高效解决子区间问题的算法技巧，常用于：
1.寻找满足条件的最短/最长连续子数组
2.统计满足某些性质的子区间数量
时间复杂度通常从暴力 O(n²) 优化到 O(n)
2. 算法框架

int left = 0, right = 0;  // 初始化窗口边界
while (right < n) {// 1. 扩大右边界，将a[right]加入窗口update(window, a[right]);right++;// 2. 满足条件时，收缩左边界while (is_valid(window)) {// 更新答案（如最小长度）ans = min(ans, right - left);// 移除a[left]并移动左边界remove(window, a[left]);left++;}
}

视频讲解见下方

尺取法

Problem A:尺取Language
和 Problem G：尺取 Jessica Reading Problem
Problem F：林大实验林场–尺取法
是同一个

#include<bits/stdc++.h>
using namespace std;
int a[1000005];
int main()
{int t,n,s,i,j=0,k=0,sum=0,c;unordered_set<int>set;scanf("%d",&n);for(i=0;i<n; i++){scanf("%d",&a[i]);set.insert(a[i]);}j=set.size();unordered_map<int,int>map;   //不能使用std::mapint l=0,r=0,ans=1000005;while(r<n){if(map[a[r]]==0) sum++;map[a[r]]++;r++;while(sum==j){ans=min(ans,r-l);map[a[l]]--;if(map[a[l]]==0) sum--;l++;}}printf("%d\n",ans);return 0;
}

标准尺取法的应用（寻找最短区间问题），但本题要注意使用std::unordered_map。以下是二者区别：
为什么 std::map 比 std::unordered_map 慢？
std::map 和 std::unordered_map 都是 C++ STL 提供的关联容器，用于存储键值对（key-value），但它们的底层实现不同，导致时间复杂度不同：

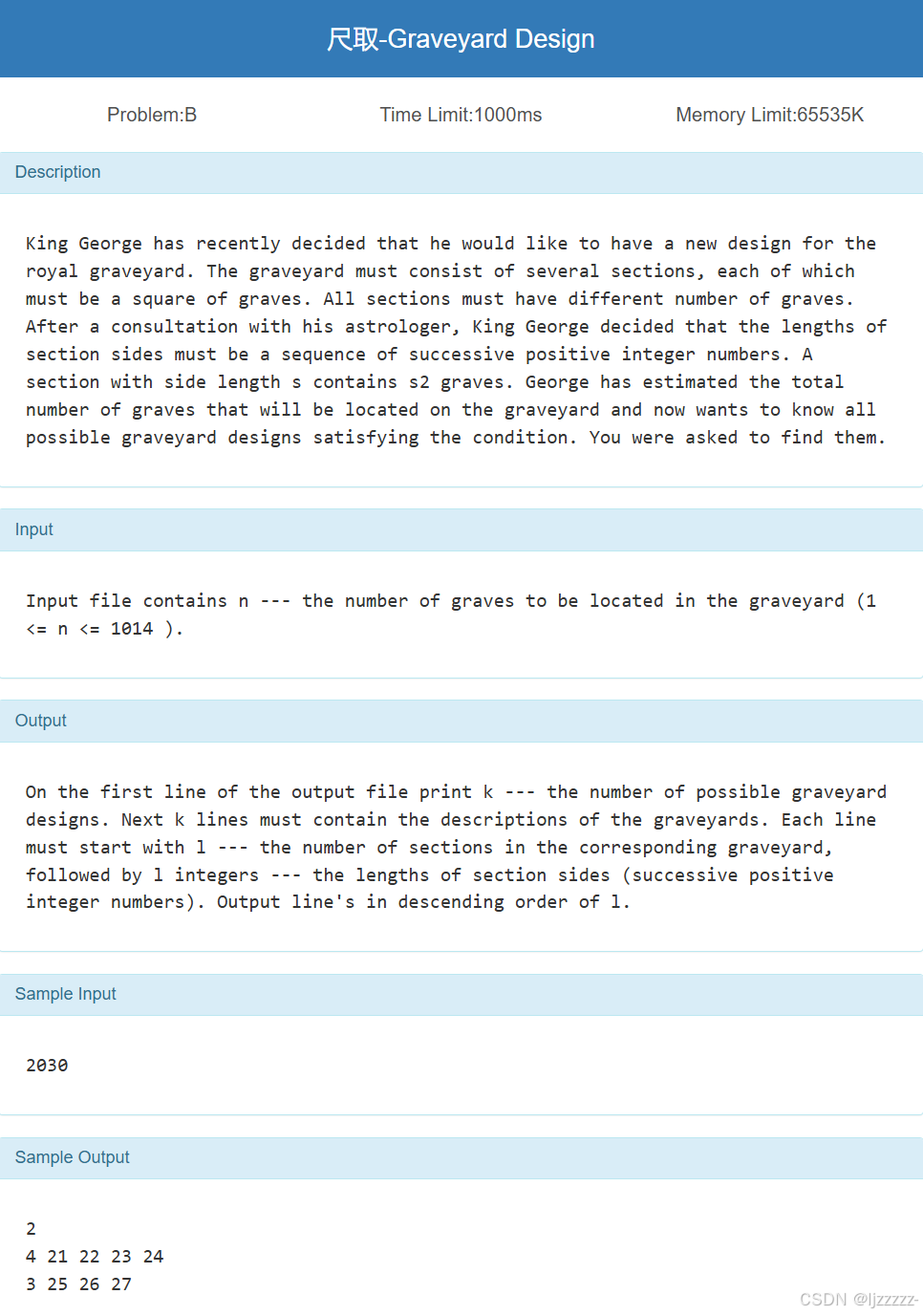
Problem B:尺取-Graveyard Design

#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
vector <pair<ll,ll> > ans;
bool compare(const pair<ll,ll>& a,const pair<ll,ll>& b)
{return (a.second - a.first) > (b.second - b.first);
}
int main()
{ll n;scanf("%lld",&n);ll l=1,r=1,sum=0;while(1){while(sum<n){sum+=r*r;r++;}if(sum<n) break;if(sum==n) ans.push_back(make_pair(l,r-1));sum-=l*l;l++;if(l*l>n) break;}sort(ans.begin(),ans.end(),compare);printf("%lld\n",ans.size());for(ll i=0;i<ans.size();i++){printf("%lld ",ans[i].second-ans[i].first+1);for(ll j=ans[i].first;j<=ans[i].second;j++){printf("%lld ",j);  //每一个都要加空格 }printf("\n");}return 0;
}

Problem C：尺取-Sum of Consecutive Prime Numbers

先用埃氏筛求出素数队列，然后在素数队列下进行尺取法

#include<bits/stdc++.h>
using namespace std;
typedef long long LL;
const LL maxn = 1e4+10;
int primeNum[maxn];
bool isPrime[maxn];
void getPrime(int n)
{for(int i=0;i<maxn;i++) isPrime[i]=true;for(int i=2;i<=n;i++)if(isPrime[i])for(int j=2;i*j<=n;j++) isPrime[i*j]=false;for(int i=2,j=1;i<=n;i++)if(isPrime[i]) primeNum[j++] = i;
}
int main()
{int n;getPrime(maxn-10);while(cin >> n && n){int cnt=0,i=1,j=1,sum=0;if(isPrime[n]) cnt++;while(1){while(sum<n && primeNum[j]<n) sum+=primeNum[j++];if(sum<n) break;if(sum==n) cnt++;sum-=primeNum[i++];}cout<<cnt<<endl;}return 0;
}

Problem D：尺取-序列

标准尺取题

#include<bits/stdc++.h>
using namespace std;
int m,n,s;
int q[100005];
int main()
{scanf("%d",&m);while(m--){scanf("%d%d",&n,&s);for(int i=0;i<n;i++) scanf("%d",&q[i]);int l=0,r=0,ans=n+1,sum=0;while(1){while(r<n && sum<s) sum+=q[r++];if(sum<s) break;ans=min(ans,r-l);sum-=q[l++];}if(ans==n+1) printf("0\n");else printf("%d\n",ans);}return 0;
}

Problem E：尺取-字符串

#include <bits/stdc++.h>
using namespace std; 
const int N = 1e6 + 5;
char s[N];
int cnt[255];
int main()
{int i, j, n, m, tot = 0, ans = 1e9;scanf("%s",s+1);n = strlen(s+1);j = 1; cnt[s[1]]++; tot = 1;for(i = 2; i <= n; i++){if(!cnt[s[i]]) tot++;cnt[s[i]]++;while(cnt[s[j]]>1){cnt[s[j]]--;j++;}if(tot==26) ans=min(ans,i-j+1);}printf("%d",ans);return 0;
}