机器学习中的关键术语及其含义
神经元及神经网络
机器学习中的神经网络是一种模仿生物神经网络的结构和功能的数学模型或计算模型。它是指按照一定的规则将多个神经元连接起来的网络。
神经网络是一种运算模型,由大量的节点(或称神经元)之间相互联接构成。每个节点代表一种特定的输出函数,称为激励函数。

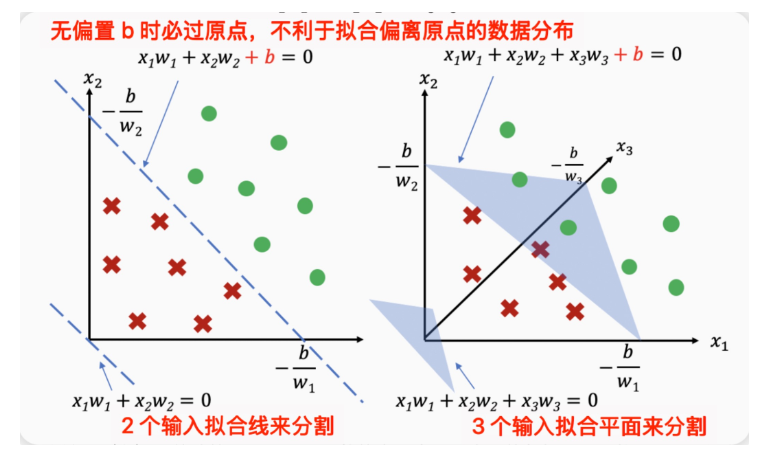
偏置项的作用
多层感知机
多个神经元可以组合一起,形成多层感知机。多层感知器(Multi-Layer Perceptron,MLP):通过叠加多层全连接层来提升网络的表达能力。相比单层网络,多层感知器有很多中间层的输出并不暴露给最终输出,这些层被称为隐含层(Hidden Layers)。

下图描述了神经网络构建过程中的基本细节。
- - 基类需要初始化训练参数、管理参数状态以及定义计算过程;神经网络模型需要实现对神经网络层和神经网络层参数管理的功能。
- - 在机器学习编程库中,承担此功能有MindSpore的Cell、PyTorch的Module。Cell和Module是模型抽象方法也是所有网络的基类。现有模型抽象方案有两种,
- 一种是抽象出两个方法分别为Layer(负责单个神经网络层的参数构建和前向计算),Model(负责对神经网络层进行连接组合和神经网络层参数管理);
- 另一种是将Layer和Model抽象成一个方法,该方法既能表示单层神经网络层也能表示包含多个神经网络层堆叠的模型,Cell和Module就是这样实现的。

样本,目标函数,损失函数,特征及训练
- 样本(Sample)
定义:样本是数据集中的单个实例或数据点,通常由一组特征(自变量)和一个标签(因变量)组成。
举例:在房价预测中,一个样本可能包含房屋的面积、卧室数量、位置等特征,以及对应的房价标签。
- 标签(Label)
定义:标签是与样本关联的目标值或类别,用于监督学习中指导模型学习。
举例:在垃圾邮件分类中,标签可以是“垃圾邮件”或“非垃圾邮件”。
- 自变量(Independent Variable)
定义:自变量是用于预测或解释目标变量的输入特征,也称为特征或预测变量。
举例:在预测学生成绩时,自变量可以是学习时间、家庭收入等。
- 目标函数(Target Function)
定义:目标函数是模型训练过程中优化的目标,通常由损失函数构成,用于衡量模型性能。
举例:在线性回归中,目标函数是最小化均方误差(MSE)。
- 损失函数(Loss Function)
定义:损失函数用于量化模型预测值与真实值之间的差异,是目标函数的核心组成部分。用来衡量单个样本中计算值与标签值的差异。
举例:在分类问题中,常用的损失函数是交叉熵损失。
- 代价函数(Cost Function)
定义:代价函数是损失函数在所有样本上的平均值,用于衡量模型在整个数据集上的性能。损失函数与代价函数的区别在于,损失函数只适用于单个训练样本,而代价函数是参数的总代价。
举例:在逻辑回归中,代价函数是交叉熵损失的平均值。
- 特征(Feature)
定义:特征是描述样本的属性或变量,用于模型的输入。
举例:在图像分类中,特征可以是像素值或提取的边缘信息。
- 模型(Model)
定义:模型是通过机器学习算法从数据中学习到的数学表示,用于对新数据进行预测。
举例:决策树模型可以根据输入特征决定输出类别。
- 训练数据(Training Data)
定义:训练数据是用于训练机器学习模型的数据集,通常包含输入特征和对应的标签。
举例:在预测房价的模型中,训练数据可能包括房屋特征及其相应的价格。
- 测试数据(Testing Data)
定义:测试数据是用于评估模型在未知数据上表现的数据集。
举例:在训练垃圾邮件过滤器后,可以在以前从未见过的电子邮件上对其进行测试。
- 正则化(Regularization)
定义:正则化是一种技术,用于防止模型过度拟合,通过在损失函数中添加惩罚项来限制模型的复杂度。
举例:L2正则化通过在损失函数中添加权重平方和来限制权重的大小。
- 学习率(Learning Rate)
定义:学习率是一个超参数,控制模型权重相对于损失梯度的更新程度。
举例:在神经网络中,学习率决定了模型在训练期间从错误中学习的速度。
- Epoch
定义:一个epoch是指在模型训练过程中对整个训练数据集进行一次完整的遍历。
举例:如果有1000个训练样本,1个epoch意味着模型已经看过所有1000个样本一次。
- 超参数(Hyperparameter)
定义:超参数是在训练之前设置的参数,用于控制学习过程和模型结构。
举例:学习率、批量大小(batch size)、神经网络的层数和每层的神经元数量等都是常见的超参数。
- 回归问题:回归问题是机器学习中的一种任务,其目标是预测一个连续值作为输出。
- 目标变量:回归问题中的目标变量是连续的,可以取任何实数值。
- 特征:用于预测目标变量的输入变量,可以是连续的或离散的。
- 线性回归问题:线性回归是一种回归模型,假设输入变量(特征)和输出变量(目标)之间存在线性关系。它通过找到一条最佳拟合直线来模拟这种关系。
- 逻辑回归问题:逻辑回归是一种用于分类问题的统计方法,尽管名字中包含“回归”,但它实际上是一种分类算法。
定义:它通过逻辑函数(Sigmoid函数)将输入特征映射到0到1之间的概率值,表示属于某个类别的可能性。
- 训练:找到一组参数值Weight(面积)、Weight(age)、b,能够使得在给定的训练数据集合上,所产生的集体误差最小。
- 预测:当用户给定房屋面积、年龄后,能够给出对应的房价。这个房价越贴近于真实值,表示模型效果越好。
- 数据分布:训练的过程就是找到一个函数,能够匹配数据的分布的过程。

非线性激活函数
激活函数:人工神经网络中的一个关键组件,它负责将神经元的输入信号转换为输出信号,从而引入非线性特性。如果没有激活函数,神经网络的每一层都只是线性变换的叠加,整个网络将退化为一个简单的线性模型,无法拟合复杂的数据分布或解决非线性问题。
讨论1:为什么激活函数必须要有非线性的?

激活函数对模型至关重要:引入非线性,增强表达能力,控制输出范围,促进梯度传播,模拟生物神经元的激活机制。
常见的激活函数
Sigmoid函数:将输入映射到(0,1)之间,常用于二分类问题,但容易导致梯度消失问题。
Tanh函数:将输入映射到(−1,1)之间,解决了Sigmoid的零均值问题,但仍存在梯度消失问题。
ReLU函数:在输入为正时输出输入值,输入为负时输出0,计算简单且能有效缓解梯度消失问题,但可能导致“神经元死亡”问题。

Softmax函数:将输入映射为概率分布,常用于多分类问题的输出层。

典型的模型训练过程

反向传播机制
用一个实际的例子来理解机器学习和反向传播

学习率的影响

正向传播和反向传播的计算

由单个样本至多个样本的反向传播的计算

链式法则

参数权重矩阵和个别参数更新的关系:如上图是函数的变量是以矩阵的形式体现的,但在计算参数偏导时是具体到每个参数的,所以注意求偏导时函数要展开成针对参数矩阵里特定的参数。
- 反向传播的顺序;梯度是一步一步进行传播的。从计算可以看到,前面网络层的参数更新依赖后面网络层的参数,所以参数如果过小,经过连乘效应,前面的参数基本得不到更新,这就是所谓的参数消失。
- 网络保存着前向传播计算得到的值,包括隐藏层,所以在反向传播计算时候可以直接拿到这些值,不过这也需要存储空间。
