比较5点结构的减一对称性
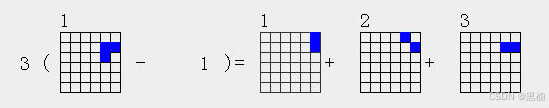
3(3a1-1)=2a1+2a2+2a3
3a1减一可以得到3个不同的2点结构,2a1,2,3.所以3a1的3个点有3种不同的对称性。
| 1 | A |
| 1 | 0 |
如果把3a1中的A看作是不动的,则剩余的两个点将按照2a1的方式运动,符合这种运动的函数可能有很多,比如把所有这些满足2a1的函数写为f2a1.结构3a1就对应函数组合f3a1,则f3a1中的点x1可以用剩余的两个点x2,x3的运动方式f2a1去定义
![]()
同样的方法计算x2,x3则有
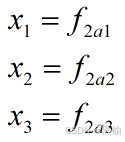
3a1中的3个点可以彼此独立。

4(4a2-1)=3a4+3a3+3a5+3a1
有1个4点结构可以被分解为4个不同的3点结构
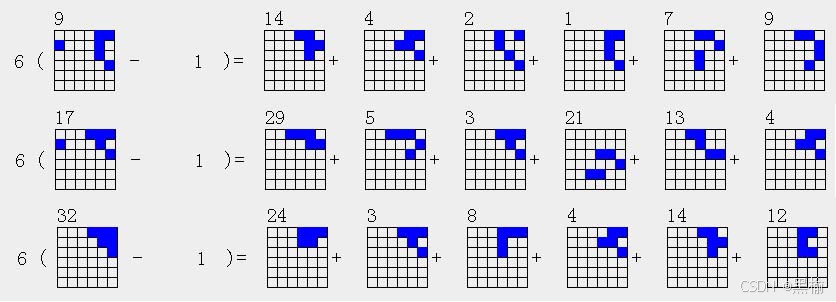
6(6a9-1)=5a14+5a4+5a2+5a1+5a7+5a9
6(6a17-1)=5a29+5a5+5a3+5a21+5a13+5a4
6(6a32-1)=5a24+5a3+5a8+5a4+5a14+5a12
有3个6点结构可以被分解为6个不同的5点结构

| 7(7a19-1)=6a1+6a6+6a9+6a13+6a23+6a24+6a32 |
| 7(7a26-1)=6a4+6a5+6a9+6a14+6a19+6a26+6a39 |
| 7(7a32-1)=6a6+6a8+6a9+6a17+6a39+6a40+6a44 |
| 7(7a43-1)=6a8+6a14+6a16+6a17+6a34+6a49+6a53 |
| 7(7a60-1)=6a9+6a14+6a15+6a37+6a39+6a40+6a45 |
| 7(7a62-1)=6a8+6a14+6a18+6a24+6a32+6a39+6a41 |
| 7(7a69-1)=6a8+6a14+6a17+6a23+6a25+6a33+6a40 |
| 7(7a165-1)=6a17+6a32+6a41+6a44+6a45+6a62+6a78 |
有8个7点结构可以被分解为7个不同的6点结构


| 8(8a44-1)=7a3+7a10+7a19+7a26+7a30+7a57+7a62+7a64 |
| 8(8a73-1)=7a10+7a16+7a26+7a32+7a43+7a97+7a101+7a108 |
| 8(8a74-1)=7a5+7a18+7a19+7a32+7a41+7a62+7a69+7a93 |
| 8(8a86-1)=7a10+7a21+7a25+7a26+7a32+7a35+7a40+7a69 |
| 8(8a100-1)=7a13+7a19+7a32+7a40+7a62+7a66+7a69+7a137 |
| 8(8a116-1)=7a13+7a19+7a30+7a32+7a49+7a111+7a129+7a165 |
| 8(8a124-1)=7a24+7a25+7a26+7a35+7a37+7a51+7a60+7a111 |
| 8(8a139-1)=7a13+7a19+7a39+7a60+7a62+7a80+7a111+7a127 |
| 8(8a160-1)=7a26+7a37+7a44+7a60+7a86+7a101+7a108+7a121 |
| 8(8a184-1)=7a32+7a39+7a43+7a60+7a97+7a130+7a158+7a162 |
| 8(8a186-1)=7a16+7a43+7a44+7a57+7a69+7a70+7a82+7a101 |
| 8(8a203-1)=7a32+7a34+7a39+7a49+7a60+7a62+7a67+7a165 |
| 8(8a233-1)=7a32+7a39+7a40+7a60+7a69+7a85+7a111+7a190 |
| 8(8a246-1)=7a26+7a35+7a50+7a57+7a60+7a103+7a111+7a139 |
| 8(8a275-1)=7a33+7a43+7a69+7a106+7a111+7a121+7a162+7a197 |
| 8(8a292-1)=7a40+7a49+7a62+7a69+7a75+7a111+7a140+7a165 |
| 8(8a294-1)=7a43+7a69+7a73+7a82+7a111+7a130+7a162+7a164 |
| 8(8a317-1)=7a32+7a60+7a62+7a77+7a98+7a107+7a165+7a177 |
| 8(8a343-1)=7a43+7a62+7a97+7a100+7a121+7a129+7a161+7a165 |
有19个8点结构可以被分解为8个不同的7点结构
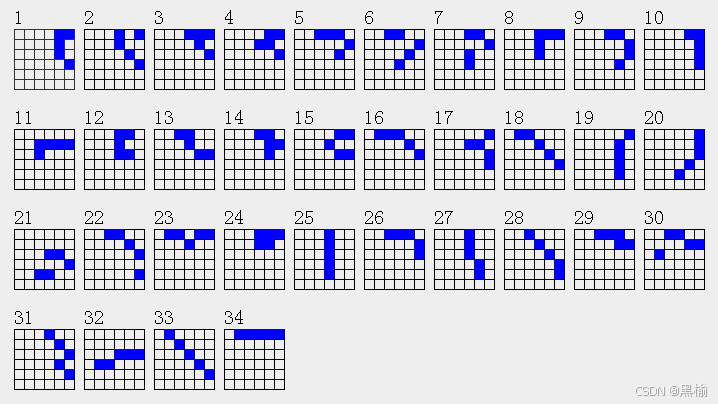
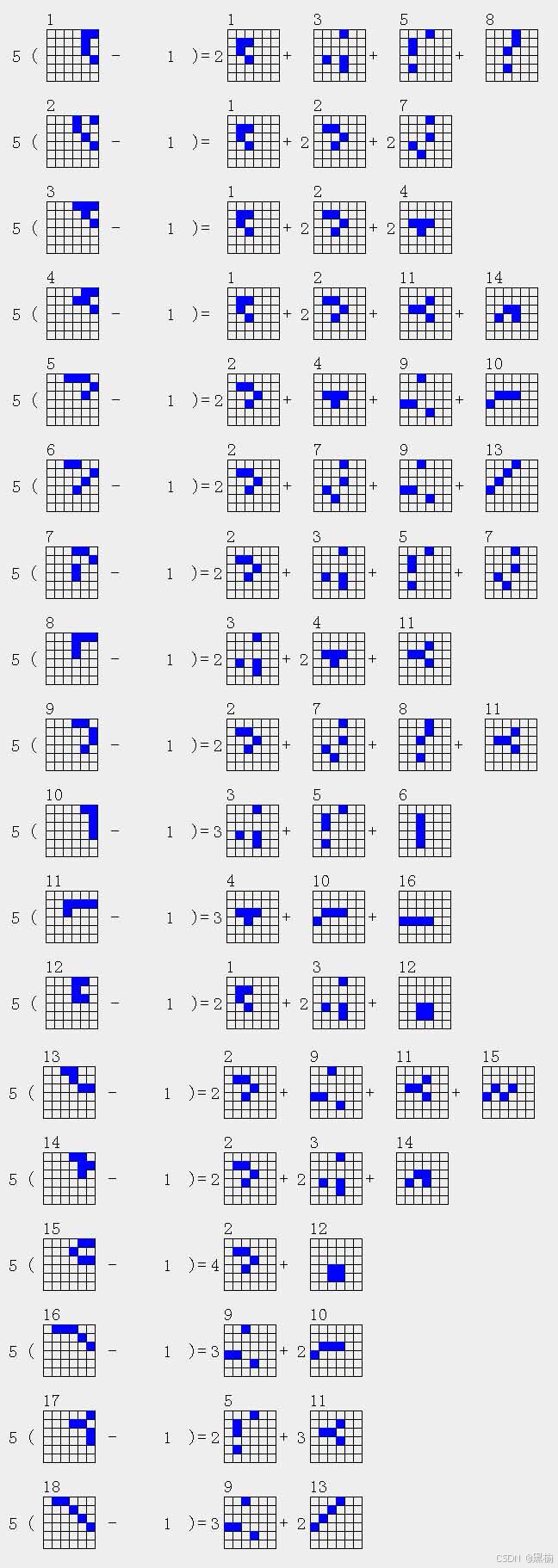
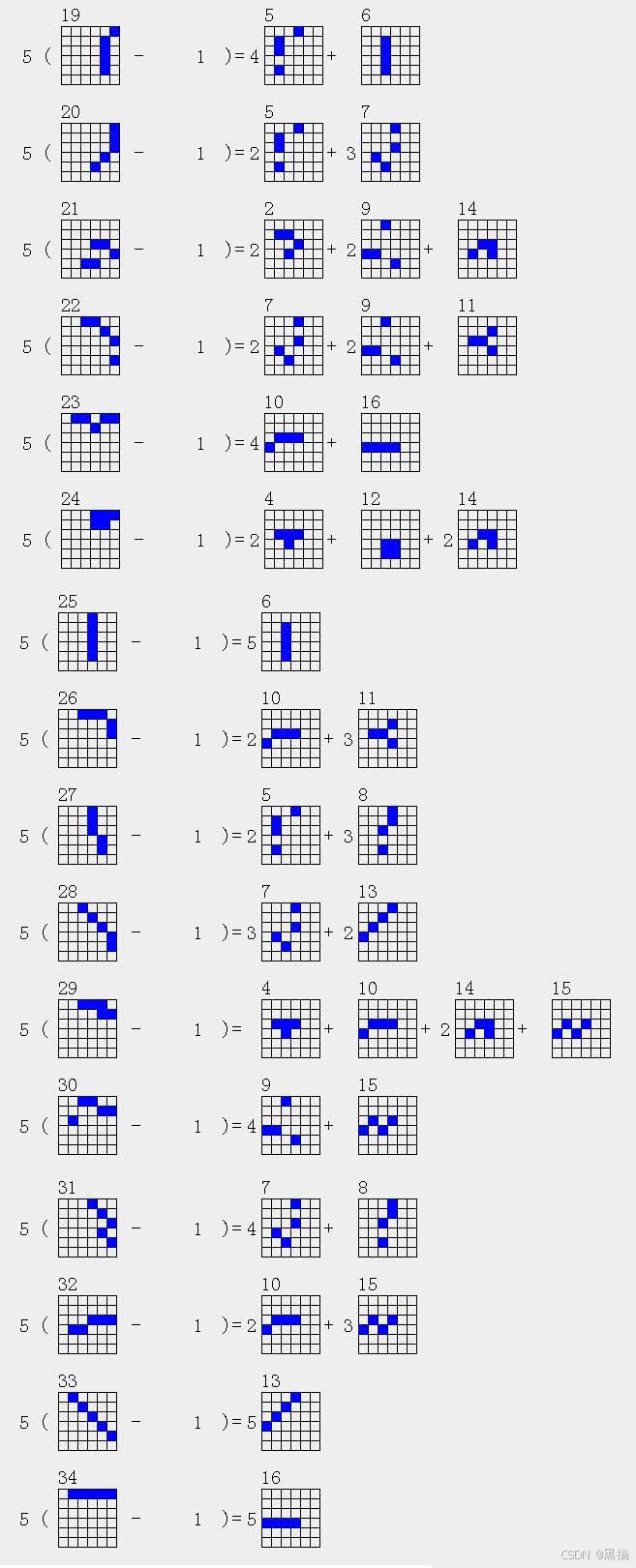
但在所有34个5点结构中,没有任何一个5点结构可以被分解为5个不同的4点结构,平面上的5点不可能有5种不同的减一对称性,
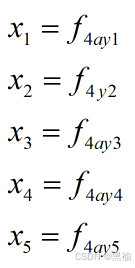
所以如果用对称性去定义这5个点,y1,2,3,4,5不可能相互独立,至少有2个彼此是相同的。平面上的5个点,不论如何分布,其中至少有2个点彼此无法区分。
