当前位置：首页 > news >正文

【Python 算法零基础 4.排序 ⑤ 归并排序】

news 2025/11/2 15:38:14

你什么都要刨根问底，却又接受不了真相带来的冲击

—— 25.5.23

选择排序回顾

① 遍历数组：从索引 0 到 n-1（n 为数组长度）。

② 每轮确定最小值：假设当前索引 i 为最小值索引 min_index。从 i+1 到 n-1 遍历，若找到更小元素，则更新 min_index。

③ 交换元素：若 min_index ≠ i，则交换 arr[i] 与 arr[min_index]。

'''
① 遍历数组：从索引 0 到 n-1（n 为数组长度）。② 每轮确定最小值：假设当前索引 i 为最小值索引 min_index。从 i+1 到 n-1 遍历，若找到更小元素，则更新 min_index。③ 交换元素：若 min_index ≠ i，则交换 arr[i] 与 arr[min_index]。
'''def selectionSort(arr: List[int]):n = len(arr)for i in range(n):min_index = ifor j in range(i + 1, n):if arr[min_index] > arr[j]:min_index = jif min_index != i:arr[min_index], arr[j] = arr[j], arr[min_index]return arr

插入排序回顾

① 遍历未排序元素：从索引 1 到 n-1。

② 保存当前元素：将 arr[i] 存入 current。

③ 元素后移：从已排序部分的末尾（索引 j = i-1）向前扫描，将比 current 大的元素后移。直到找到第一个不大于 current 的位置或扫描完所有元素。

④ 插入元素：将 current 放入 j+1 位置。

'''
① 遍历未排序元素：从索引 1 到 n-1。② 保存当前元素：将 arr[i] 存入 current。③ 元素后移：从已排序部分的末尾（索引 j = i-1）向前扫描，将比 current 大的元素后移。直到找到第一个不大于 current 的位置或扫描完所有元素。④ 插入元素：将 current 放入 j+1 位置。
'''
def insertSort(arr: List[i]):n = len(arr)for i in range(n):current = arr[i]j = i - 1while current < arr[j] and j >0:arr[j+1] = arr[j]j -= 1arr[j + 1] = currentreturn arr

冒泡排序回顾

① 初始化：设数组长度为 n。

② 外层循环：遍历 i 从 0 到 n-1（共 n 轮）。

③ 内层循环：对于每轮 i，遍历 j 从 0 到 n-i-2。

④ 比较与交换：若 arr[j] > arr[j+1]，则交换两者。

⑤ 结束条件：重复步骤 2-4，直到所有轮次完成。

'''
① 初始化：设数组长度为 n。② 外层循环：遍历 i 从 0 到 n-1（共 n 轮）。③ 内层循环：对于每轮 i，遍历 j 从 0 到 n-i-1。④ 比较与交换：若 arr[j] > arr[j+1]，则交换两者。⑤ 结束条件：重复步骤 2-4，直到所有轮次完成。
'''
def bubbleSort(arr: List[int]):n = len(arr)for i in range(n):for j in range(n - i - 1):if arr[j] > arr[j + 1]:arr[j], arr[j + 1] = arr[j + 1], arr[j]return arr

计数排序回顾

① 初始化：设数组长度为 n，元素最大值为 r。创建长度为 r+1 的计数数组 count，初始值全为 0。

② 统计元素频率：遍历原数组 arr，对每个元素 x，将 count[x] 加 1。

③ 重构有序数组：初始化索引 index = 0。遍历计数数组 count，索引 v 从 0 到 r，若 count[v] > 0，则将 v 填入原数组 arr[index]，并将 index 加 1。count[v] - 1，重复此步骤直到 count[v] 为 0。

④ 结束条件：当计数数组遍历完成时，排序结束。

'''
输入全为非负整数，且所有元素 ≤ r① 初始化：设数组长度为 n，元素最大值为 r。创建长度为 r+1 的计数数组 count，初始值全为 0。② 统计元素频率：遍历原数组 arr，对每个元素 x，将 count[x] 加 1。③ 重构有序数组：初始化索引 index = 0。遍历计数数组 count，索引 v 从 0 到 r，
若 count[v] > 0，则将 v 填入原数组 arr[index]，并将 index 加 1。
count[v] - 1，重复此步骤直到 count[v] 为 0。④ 结束条件：当计数数组遍历完成时，排序结束。
'''
def countingSort(arr: List[int], r: int):# count = [0] * len(r + 1)count = [0 for i in range(r + 1)]for x in arr:count[x] += 1index = 0for v in range(r + 1):while count[v] > 0:arr[index] = vindex += 1count[v] -= 1return arr

一、引言

归并是一种常见的算法思想，:在许多领域都有广泛的应用。归并排序的主要目的是将两个已排序的序列合并成一个有序的序列。

二、算法思想

当然，对于一个非有序的序列，可以拆成两个非有序的序列，然后分别调用归并排序，然后对两个有序的序列再执行合并的过程。所以这里的“归”其实是递归，“并”就是合并。

整个算法的执行过程用mergeSort(arr[], l, r)描述，代表当前待排序数组 arr，左区间下标 l，右区间下标 r，分以下几步:

① 计算中点 mid = (l + r) / 2;

② 递归调用 mergeSort(arr[], l, mid) 和 mergeSort(arr[], mid+1, r)；

③ 上一步的两个有序数组进行有序合并，再存储到 arr[l : r]；

调用时，调用 mergeSort(arr[], 0, n-1) 就能得到整个数组的排序结果了

归并排序对应的数据结构本质上是一颗二叉树

三、算法分析

1.时间复杂度

我们假设「比较」和「赋值」的时间复杂度为O(1)。

「归并排序」算法的最重要的子程序：O(n)的合并，然后解析这个归并排序算法。

给定两个大小为n1 和 n2的排序数组A 和 B，我们可以在O(n)时间内将它们有效地归并成一个大小为n = n1 + n2的组合排序数组。可以通过简单地比较两个数组的前面的元素，并始终取两个中较小的一个来实现的。

由于每次都是对半切，所以整个归并过程类似于一颗二叉树的构建过程，次数就是二叉树的高度，即O(log2n)，所以归并排序的时间复杂度为O(n*log2n)

2.空间复杂度

由于归并排序在归并过程中需要额外的一个「辅助数组」，并且最大长度为原数组长度，所以「归并排序」的空间复杂度为O(n)

3.算法的优缺点

Ⅰ、算法的优点

① 稳定性：归并算法是一种稳定的排序算法，这意味着在排序过程中，相同元素的相对顺序保持不变。

② 可扩展性：归并算法可以很容易地扩展到并行计算环境中，通过并行归并来提高排序效率

Ⅱ、算法的缺点

① 额外空间：归并算法需要使用额外的辅助空间来存储合并后的结果，这对于内存受限的情况可能是一个问题。

② 复杂性：相比于其它一些简单的排序，归并算法的实现相对复杂

四、实战练习

912. 排序数组

给你一个整数数组 nums，请你将该数组升序排列。

你必须在 不使用任何内置函数 的情况下解决问题，时间复杂度为 O(nlog(n))，并且空间复杂度尽可能小。

示例 1：
输入：nums = [5,2,3,1]
输出：[1,2,3,5]
示例 2：
输入：nums = [5,1,1,2,0,0]
输出：[0,0,1,1,2,5]
提示：

1 <= nums.length <= 5 * 104
-5 * 104 <= nums[i] <= 5 * 104

算法与思路

① 分割阶段（Divide）

Ⅰ、基准情况：若数组长度 ≤ 1，直接返回（已有序）。

Ⅱ、分割数组：计算中间索引 mid，将数组分为左半部分 left = arr[:mid] 和右半部分 right = arr[mid:]。

Ⅲ、递归排序：对左半部分 left 递归调用 mergeSort。对右半部分 right 递归调用 mergeSort。

② 合并阶段（Merge）

Ⅰ、初始化：创建空列表 res 存储合并结果，指针 i 和 j 分别初始化为 0（指向 left 和 right 的起始位置）。

Ⅱ、比较与合并：当 i < len(left) 且 j < len(right) 时，比较 left[i] 和 right[j]：若 left[i] < right[j]，将 left[i] 加入 res，i += 1。否则，将 right[j] 加入 res，j += 1。

Ⅳ、处理剩余元素：若 left 有剩余元素（i < len(left)），将 left[i:] 全部追加到 res。若 right 有剩余元素（j < len(right)），将 right[j:] 全部追加到 res。

③ 递归返回与整合

每次递归返回合并后的有序子数组，最终 sortArray 返回整个排序后的数组。

class Solution:def merge(self, left, right):res = []i = j = 0n1 = len(left)n2 = len(right)while i < n1 and j < n2:if left[i] < right[j]:res.append(left[i])i += 1else:res.append(right[j])j += 1while i < n1:res.append(left[i])i += 1while j < n2:res.append(right[j])j += 1return resdef mergeSort(self, arr: List[int]):if len(arr) <= 1:return arrmid = len(arr) // 2left = self.mergeSort(arr[:mid])right = self.mergeSort(arr[mid:])return self.merge(left, right)def sortArray(self, nums: List[int]) -> List[int]:return self.mergeSort(nums)

LCR 077. 排序链表

给定链表的头结点 head ，请将其按升序排列并返回 排序后的链表 。

示例 1：
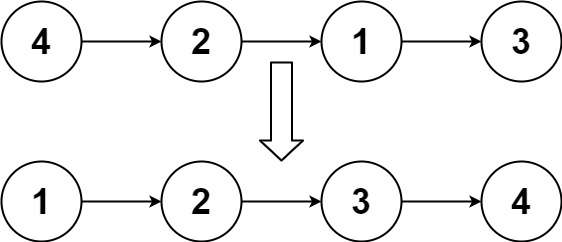
输入：head = [4,2,1,3]
输出：[1,2,3,4]
示例 2：
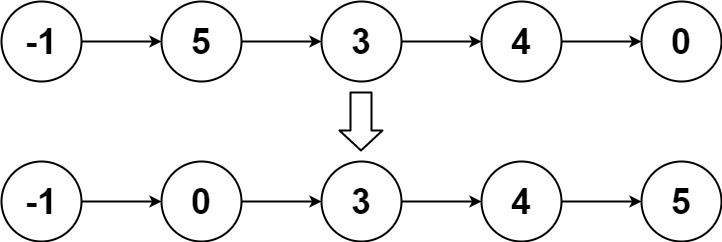
输入：head = [-1,5,3,4,0]
输出：[-1,0,3,4,5]
示例 3：
输入：head = []
输出：[]
提示：

链表中节点的数目在范围 [0, 5 * 104] 内
-105 <= Node.val <= 105

进阶：你可以在 O(n log n) 时间复杂度和常数级空间复杂度下，对链表进行排序吗？

思路与算法

① 递归终止条件

Ⅰ、判断条件：若链表为空 (head is None) 或仅有一个节点 (head.next is None)，直接返回当前链表（无需排序）。

Ⅱ、作用：作为分治的基准情况，终止递归。

② 分割链表（Divide）

Ⅰ、快慢指针找中点：初始化 slow = head，fast = head.next。快指针 fast 每次移动两步，慢指针 slow 每次移动一步。当 fast 到达链表末尾时，slow 指向链表的中间节点（或左中节点）。

Ⅱ、分割操作：将链表分为两部分：head（原链表左半部分）和 head2 = slow.next（右半部分）。断开 slow.next（设为 None），使两子链表独立。

③ 递归排序子链表

Ⅰ、左半部分排序：对 head 递归调用 mergesort，返回排序后的左链表。

Ⅱ、右半部分排序：对 head2 递归调用 mergesort，返回排序后的右链表。

④ 合并有序链表（Conquer）

Ⅰ、初始化哑节点：创建 zero（哑节点）和 current 指针，简化合并操作。

Ⅱ、比较与合并：当 head1 和 head2 均非空时：若 head1.val <= head2.val，将 head1 接到 current.next，head1 后移。否则，将 head2 接到 current.next，head2 后移。current 指针后移。

Ⅲ、处理剩余节点：将非空的 head1 或 head2 直接接到 current.next（剩余部分已有序）。

5. 返回合并结果

最终返回 zero.next，即合并后的有序链表头节点。

# Definition for singly-linked list.
# class ListNode:
#     def __init__(self, val=0, next=None):
#         self.val = val
#         self.next = next
class Solution:def mergesort(self, head: ListNode):if head is None or head.next is None:return headslow, fast = head, head.nextwhile fast and fast.next:slow = slow.nextfast = fast.next.nexthead2 = slow.nextslow.next = Nonereturn self.merge(self.mergesort(head), self.mergesort(head2))def merge(self, head1: ListNode, head2: ListNode):zero = ListNode(-1)current = zerowhile head1 and head2:if head1.val <= head2.val:current.next = head1head1 = head1.nextelse:current.next = head2head2 = head2.nextcurrent = current.nextcurrent.next = head1 if head1 else head2return zero.nextdef sortList(self, head: Optional[ListNode]) -> Optional[ListNode]:return self.mergesort(head)