当前位置：首页 > news >正文

【数据结构】手撕归并排序（含非递归）

news 来源：原创 2025/5/14 12:22:03

一，归并排序（递归）

1，基本思想

2，思路实现

二，归并排序（非递归）

1，思路实现

2，归并排序的特性总结：

一，归并排序（递归）

1，基本思想

归并排序（MERGE-SORT）是建立在归并操作上的一种有效的排序算法,该算法是采用分治法（Divide and Conquer）的一个非常典型的应用；

将已有序的子序列合并，得到完全有序的序列；

即先使每个子序列有序，再使子序列段间有序，若将两个有序表合并成一个有序表，称为二路归并；

归并排序核心步骤：

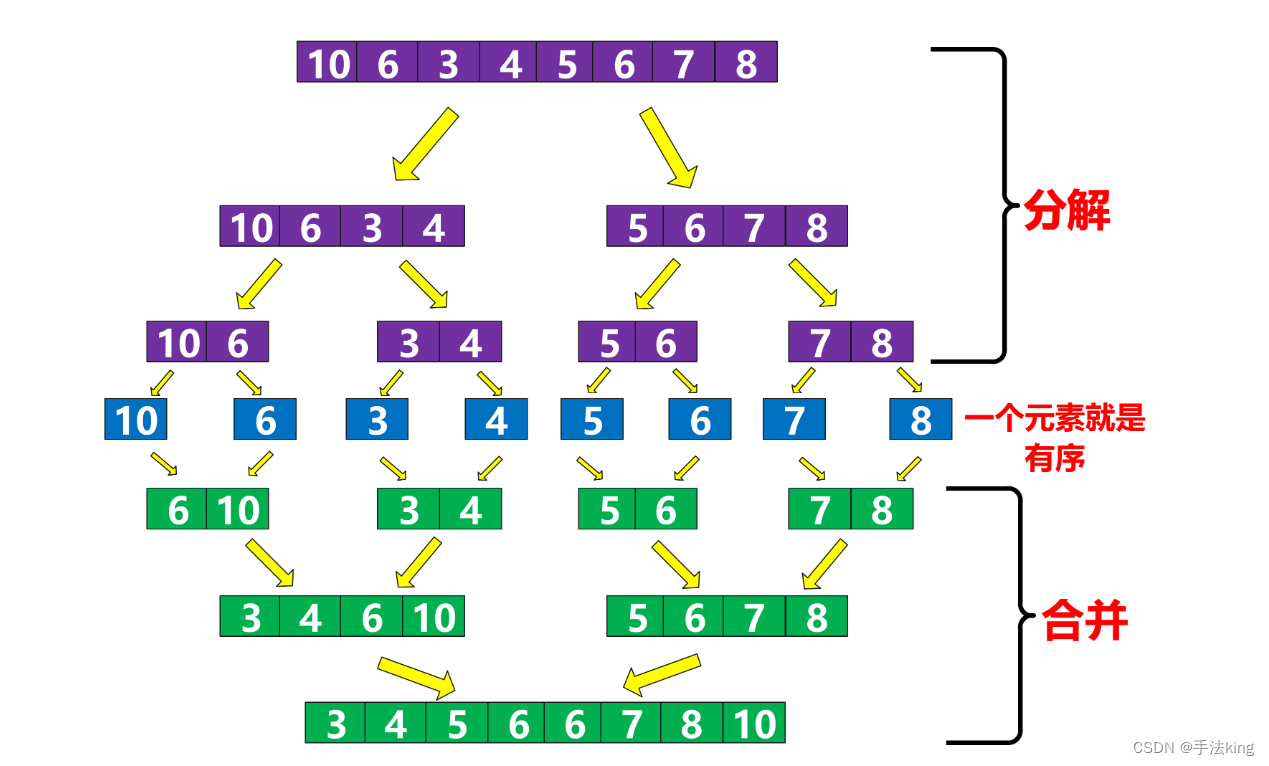
2，思路实现

这个归并排序乍一看像一颗二叉树，事实也是如此，如上图所示我们需要不断的拆分直至拆成一个元素此时就是有序的，然后再合并，合并的时候不要选择原地合并（原地合并时间复杂度很高），需要开辟与数组同等大小的空间用来存放数据；

主函数整体框架：

//归并排序
void MergerSort(int* arr, int begin, int end)
{
	if (begin >= end)
	{
		return;
	}
	//开辟同等大小数组
	int* tmp = (int*)malloc((end - begin + 1)*sizeof(int));
	//归并
	Merger(arr, tmp, begin, end);
	free(tmp);
	tmp = NULL;
}

然后我们就要开始实现 Merger 函数，是数据归并了；

把数组拆分成一个数据后开始合并，刚开始一一合并，然后二二合并，然后四四合并，直至全数组合并完；

//归并
void Merger(int* arr, int* tmp,int begin,int end)
{
	int mid = (begin + end) / 2;
	if (begin == end)
	{
		return;
	}
	//排序【begin,mid】& 【mid+1,end】
	Merger(arr, tmp, begin,mid);
	Merger(arr, tmp, mid+1, end);

	int begin1 = begin, end1 = mid;
	int begin2 = mid + 1, end2 = end;
	int i = 0;
	while (begin1 <= end1 && begin2 <= end2)
	{
		if (arr[begin1] <= arr[begin2])
		{
			tmp[i++] = arr[begin1++];
		}
		else
		{
			tmp[i++] = arr[begin2++];
		}
	}
	while(begin1 <= end1)
	{
		tmp[i++] = arr[begin1++];
	}
	while (begin2 <= end2)
	{
		tmp[i++] = arr[begin2++];
	}
	//进行拷贝
	memcpy(arr + begin, tmp, (end - begin+1)*sizeof(int));
}

然后我们运行测试一下：

可以看到是有序的，选择排序就 OK 了；

其实跟二叉树的前序遍历有异曲同工之处，前后知识都是连贯起来的；

二，归并排序（非递归）

1，思路实现

现在我们来拿捏一下非递归版的归并排序，其实也还是换汤不换药；

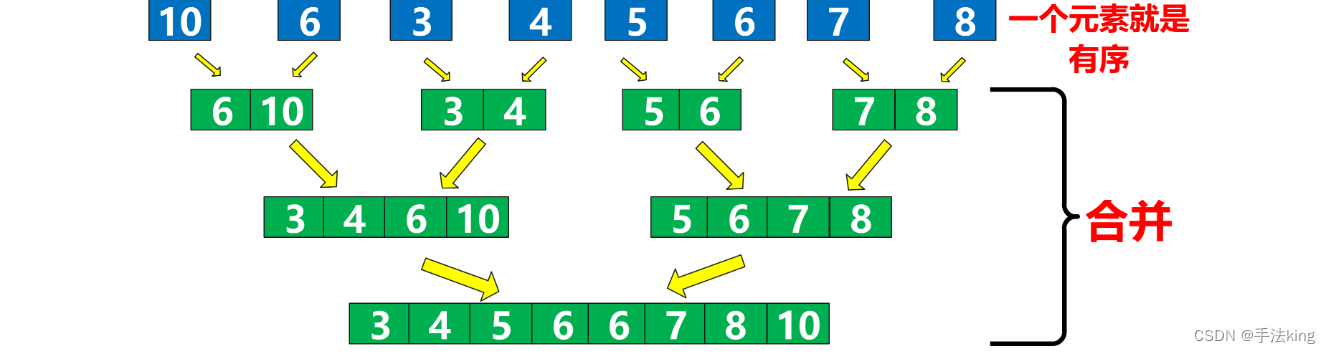
其实新思路是这个图的下半部分，我们先让数据一一合并，然后再二二合并，然后再四四合并程倍数增长，有人问如果越界了怎么办？没关系我们后面会做越界处理的；

直接上代码！

//归并排序(非递归)
void MergerSortNon(int* arr, int begin, int end)
{
	if (begin >= end)
	{
		return;
	}
	//开辟同等大小数组
	int* tmp = (int*)malloc((end - begin + 1) * sizeof(int));
	int gap = 1;
	int j = 0;
	while (gap < end)
	{
		for (j = 0; j < end; j += 2 * gap)
		{
			int begin1 = j, end1 = begin1+gap-1;
			int begin2 =end1+1, end2 = begin2+gap-1;
			int i = 0;
			//处理边界问题
			if (end1 >= end)
			{
				break;
			}
			if (end2 >end)
			{
				end2 = end;
			}
			while (begin1 <= end1 && begin2 <= end2)
			{
				if (arr[begin1] <= arr[begin2])
				{
					tmp[i++] = arr[begin1++];
				}
				else
				{
					tmp[i++] = arr[begin2++];
				}
			}
			while (begin1 <= end1)
			{
				tmp[i++] = arr[begin1++];
			}
			while (begin2 <= end2)
			{
				tmp[i++] = arr[begin2++];
			}
			//进行拷贝
			memcpy(arr + j, tmp, (end2 - j+ 1) * sizeof(int));
		}
		gap *= 2;
	}
	free(tmp);
	tmp = NULL;
}

我们来运行测试一下：