Google机器学习实践指南（梯度下降篇）

🔥 Google机器学习(6)-降低损失：梯度下降

Google机器学习实战(6)-3分钟掌握梯度下降核心原理

---

一、梯度核心概念

▲ 数学定义：
梯度是偏导数的矢量，具有两大特征：

• 方向：指向损失增长最快方向
• 大小：反映变化剧烈程度

▲ 技术本质：
通过迭代计算梯度并调整参数，寻找权重和偏差的最佳组合

---

二、梯度下降详解

1. 凸函数特性

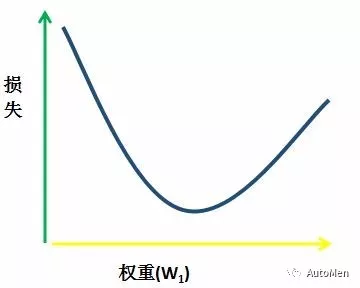
▲ 图1 回归问题的碗状损失曲线

✅ 关键特性：

• 唯一最低点（斜率=0）
• 数学上称为收敛点

2. 四步实现流程

第一阶段：参数初始化

为W1选择一个起始值（起点）

W₁ = 0 #起点可任意选择，一般设置为0

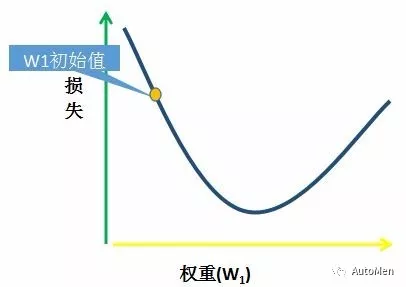
▲ 图3 梯度起始点

第二阶段：梯度计算
梯度方向图示

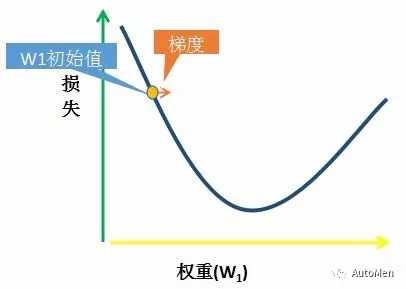
▲ 图3 负梯度方向示意图

第三阶段：参数更新
步长移动图示

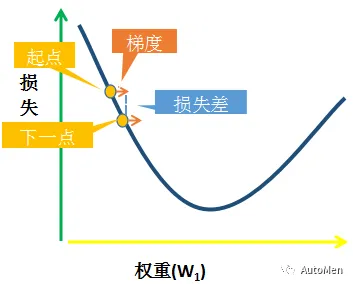
▲ 图4 单步更新过程

第四阶段：收敛判定
收敛过程图示

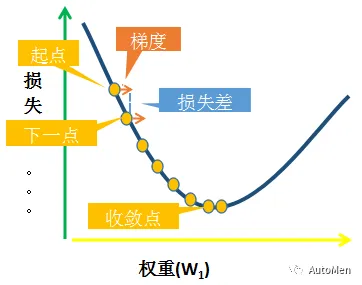
▲ 图5 完整收敛轨迹

三、关键特性

✅ 核心优势：

理论保证（凸函数必收敛）实现简单适合大规模数据

⚠️ 注意事项：

学习率需谨慎设置非凸函数可能陷入局部最优

# 技术问答 #

Q：为什么选择负梯度方向？
A：负方向指向损失下降最快路径

Q：如何判断收敛？
A：当连续迭代损失变化小于阈值时

附录：术语表

🔍 收敛
训练损失和验证损失变化趋近于零的状态

🔍 学习率
控制参数更新步长的超参数