6.12.有向无环图描述表达式
一.有向无环图(英文缩写为DAG图):

例如上述图片的两个图:
左边的图是有向无环图;
右边的图不是有向无环图,因为右边的图中存在v0可以到达v4,v4可以到达v3,v3最终又可以到达v0这样的环路,再比如v1可以到达v4,v4又可以到达v1的环路。
二.DAG图描述表达式:
1.例如:

如上图,算术表达式可以用树来表示,对树进行遍历可以得出算术表达式,详情见"5.6.二叉树的先,中,后序遍历"。
上述图片的算术表达式中存在重复的部分,比如(c+d) * e,也就是下图中红色的子树和绿色的子树,如下图:

如上图,从计算的角度来看,红色的子树和绿色的子树他们的计算结果是一样的,所以可以干掉其中的一棵子树,只保留一份,
整棵树的根结点 * 此时的右子树是(c+d) * e得到的结果,对于第二层的+,此时的右子树也是(c+d) * e得到的结果,
所以可以把 * 和 +的右指针都同时指向计算(c+d) * e的这棵树,这么做的好处是可以丢弃多余的计算(c+d) * e的树,可以节省存储空间,
最终得到的就是一个有向无环图,如下图:


如上图,计算c+d的树也存在重复的,即上述图片的绿色的子树和红色的子树,因此可以只保留一份,结果如下图:


如上图,只有结点b的树也存在重复的,即上述图片的绿色的子树和红色的子树,因此可以只保留一份,结果如下图:

如上图,最终操作数不存在重复的,因此得到了该树的DAG图。
2.408真题:

答案是A。
解析->
如上图,已经求出了题目中所给表达式的完整的树,
其中求x+y的子树存在重复的即下图中绿色的子树和红色的子树是重复的,因此可以舍弃其中的一颗,如下图:


如上图,只有x结点的这棵树也存在重复的即下图中绿色的子树和红色的子树是重复的,因此可以舍弃其中的一颗,如下图:(这一步最容易出错,因为很多时候会忽略一个结点也能当作一棵树)
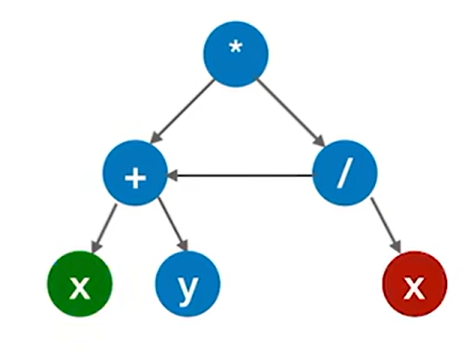

如上图,此时就得出了最终的DAG图,树最终被简化为只需要5个结点(顶点)即可,所以选A。
3.由一棵树的DAG图得出的结论:
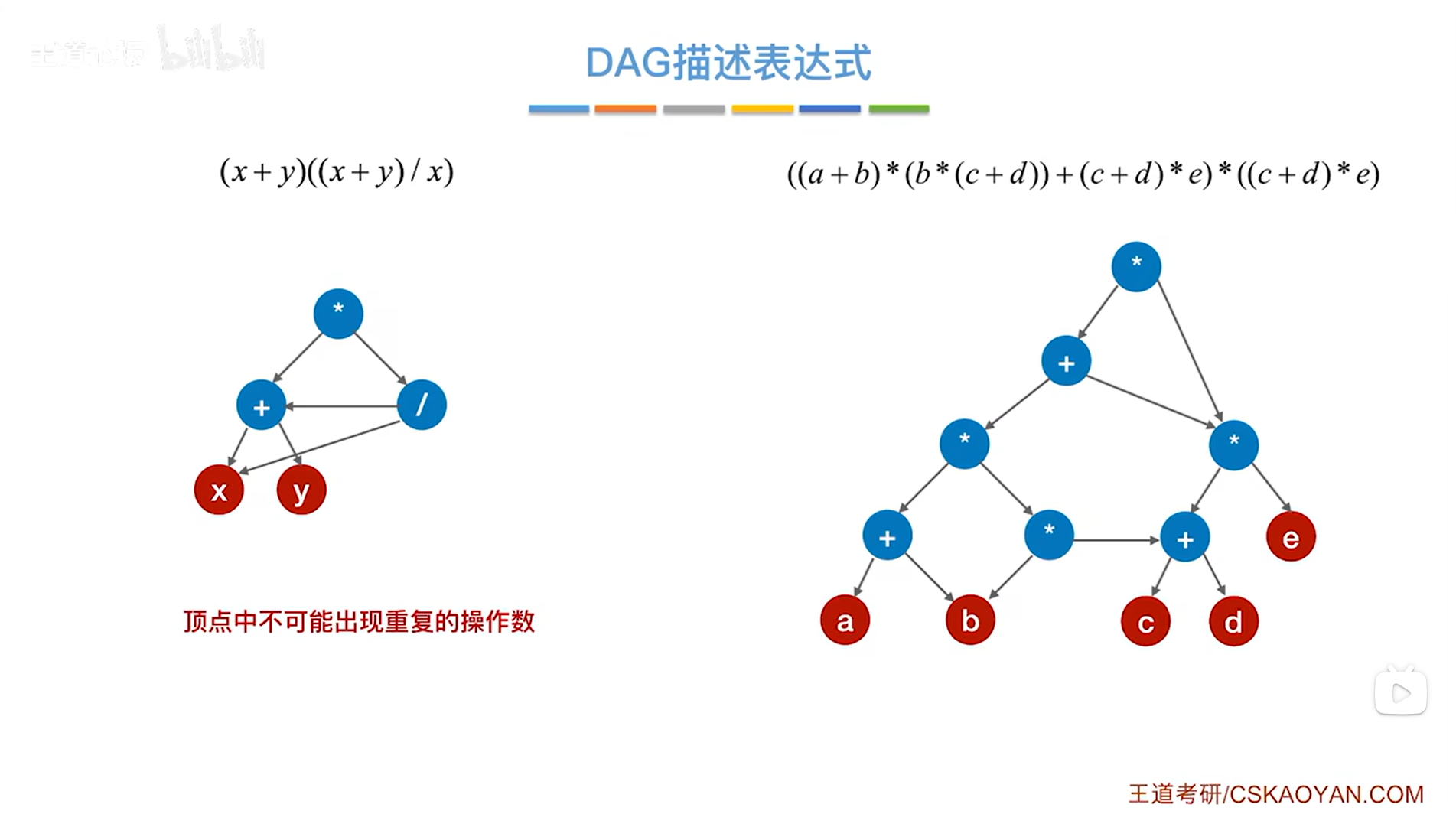
-
DAG图中的顶点内容不可能出现重复的操作数:比如上述图片中左边的表达式(x+y)((x+y)/x)中操作数只有x和y,所以x和y在DAG图中都只出现一次,右边的表达式同理
三.求DAG图的步骤:
例如:

步骤一:把表达式中各个操作数不重复地排成一排
如下图->

步骤二:标出各个运算符的生效顺序(先后顺序有点出入无所谓)
把运算符标上数字以明确生效顺序,是为了之后在构建DAG图时不遗漏任何一个运算符,这样可以防止出错,如下图->

步骤三:按运算符的生效顺序依次把存储运算符的顶点加入图中,注意"分层"
第一个生效的运算符是+,它的左边是a,右边是b,所以->

第二个生效的运算符是+,它的左边是c,右边是d,所以->

第三个生效的运算符是 * ,它的左边是b,右边是(c+d),所以->

注意:这里就需要把 * 放到+的上一层,也就是"分层",所谓的"分层",就是 * 要利用到下一层的+的运算结果才可以运算,所以要把 * 放到+的上一层

第四个生效的运算符是 * ,它的左边是(a+b),右边是(b * (c+d)),所以->

第五个生效的运算符是+,它的左边是c,右边是d,所以->

第六个生效的运算符是 * ,它的左边是(c+d),右边是e,所以->

第七个生效的运算符是+,它的左边是(a+b) * (b * (c+d)),右边是(c+d) * e,所以->

第八个生效的运算符是+,它的左边是c,右边是d,所以->

第九个生效的运算符是 * ,它的左边是(c+d),右边是e,所以->

第十个生效的运算符是 * ,它的左边是((a+b) * (b * (c+d))+(c+d) * e),右边是((c+d) * e),所以->

最终得到了完整的DAG图。
步骤四:从底向上逐层检查同层的运算符是否可以合体
这一步当中要检查哪些操作数和运算符可以合并,
由于刚开始对于各个存储操作数的顶点都只保留了一个,所以存储操作数的顶点就不需要再合并了,所以只需要一层一层地检查存储运算符的顶点哪些可以合并即可,
由于是"从底向上",倒数第一层的顶点都是存储的操作数,从倒数第二层的顶点中才开始出现运算符,所以从倒数第二层开始检查存储运算符的顶点哪些可以合并,如下图:

如上图,判断倒数第二层中存储运算符的顶点哪些可以合并,
倒数第二层中
第一个+的左边是a、右边是b,
第二个+的左边是c、右边是d,
第三个+的左边是c、右边是d,
第四个+的左边是c、右边是d,
所以第二、三、四个+可以合并,如下图:


如上图,此时倒数第二层中存储运算符的顶点全部合并完毕,继续判断倒数第三层中存储运算符的顶点哪些可以合并,
倒数第三层中
第一个 * 的左边是b、右边是(c+d),
第二个 * 的左边是(c+d)、右边是e,
第三个 * 的左边是(c+d)、右边是e,
所以第二个 * 和第三个 * 可以合并,如下图:


如上图,此时倒数第三层中存储运算符的顶点全部合并完毕,
由于倒数第四、五、六层中存储运算符的顶点都只有一个,所以一定不需要合并,因为合并至少需要两个顶点,
至此,就得到了一个最简的用有向无环图表示的算术表达式。
四.求DAG图的步骤中,步骤四中只需要检查同层的运算符的原因:

以上述图片为例,倒数第一层的顶点都是存储的操作数,从倒数第二层的顶点中才开始出现运算符,所以从倒数第二层开始检查存储运算符的顶点哪些可以合并,
对于倒数第二层中存储运算符的顶点,这些顶点中的左、右指针都是直接指向具体的操作数,
对于倒数第三层中存储运算符的顶点,这些顶点中的左、右指针一定会有指向复合的操作数,
所以倒数第三层的运算符和倒数第二层的运算符是不可能合并的,以此类推,所以只需要依次往上检查同层的运算符即可。
总之,这就是为什么在初始构造有向无环图时要把运算符分层的原因,因为只要分层了,做题就不容易乱。
五.对比:

上述图片里的两个DAG图都是表示的一个算术表达式。
六.练习:
题目:

步骤一:把表达式中各个操作数不重复地排成一排,如下图->
把存储操作数的顶点放在树的倒数第一行:

步骤二:标出各个运算符的生效顺序(先后顺序有点出入无所谓),如下图->

步骤三:按运算符的生效顺序依次把存储运算符的顶点加入图中,注意"分层",如下图->

第1个生效的运算符 * 、第2个生效的运算符 * 、第3个生效的运算符 * 都是直接对操作数a和b进行操作,所以把这三个 * 放在倒数第二层,
第4个生效的运算符 * 是基于第1个生效的运算符 * 得到的结果和第2个生效的运算符 * 得到的结果,所以第4个生效的运算符 * 要放在倒数第三层,
第5个生效的运算符 * 是基于第4个生效的运算符 * 得到的结果和第3个生效的运算符 * 得到的结果,所以第5个生效的运算符 * 要放在倒数第四层,
第6个生效的运算符 * 是基于第5个生效的运算符 * 得到的结果和操作数c,所以第6个生效的运算符 * 要放在倒数第五层,
至此,运算符全部处理完毕,DAG图初步构建完成。
步骤四:从底向上逐层检查同层的运算符是否可以合体,如下图->
这一步当中要检查哪些操作数和运算符可以合并,
由于刚开始对于各个存储操作数的顶点都只保留了一个,所以存储操作数的顶点就不需要再合并了,所以只需要一层一层地检查存储运算符的顶点哪些可以合并即可,
由于是"从底向上",倒数第一层的顶点都是存储的操作数,从倒数第二层的顶点中才开始出现运算符,所以从倒数第二层开始检查存储运算符的顶点哪些可以合并,如下图:

如上图,判断倒数第二层中存储运算符的顶点哪些可以合并,
倒数第二层中
第一个 * 的左边是a、右边是b,
第二个 * 的左边是a、右边是b,
第三个 * 的左边是a、右边是b,
所以第一、二、三个 * 可以合并,如下图:


如上图,此时倒数第二层中存储运算符的顶点全部合并完毕,
由于倒数第三、四、五层中存储运算符的顶点都只有一个,所以一定不需要合并,因为合并至少需要两个顶点,
至此,就得到了一个最简的用有向无环图表示的算术表达式。
变式:如果把运算符的生效顺序进行修改,生效顺寻如下图(用红色数字标注)

如上图,倒数第一层是所有存储操作数的顶点。

如上图,第1个生效的运算符 * 直接对操作数a和b进行操作,所以把这个 * 放在倒数第二层。

如上图,第2个生效的运算符 * 是基于第1个生效的运算符 * 得到的结果和操作数c,所以第2个生效的运算符 * 要放在倒数第三层。

如上图,第3、4个生效的运算符 * 都是直接对操作数a和b进行操作,所以把这两个 * 都放在倒数第二层。

如上图,第5个生效的运算符 * 是基于第3个生效的运算符 * 得到的结果和第4个生效的运算符 * 得到的结果,所以第5个生效的运算符 * 要放在倒数第三层。

如上图,第6个生效的运算符 * 是基于第5个生效的运算符 * 得到的结果和第2个生效的运算符 * 得到的结果,所以第6个生效的运算符 * 要放在倒数第四层。
至此,运算符全部处理完毕,DAG图初步构建完成,按照这样的运算符生效顺序来构造DAG图,这个DAG图有4层,
显然比之前的DAG图要低一层,之前生成的DAG图有5层,如下图:

接下来要进行合并,如下图:

如上图,由于是"从底向上",倒数第一层的顶点都是存储的操作数,从倒数第二层的顶点中才开始出现运算符,所以从倒数第二层开始检查存储运算符的顶点哪些可以合并,
判断倒数第二层中存储运算符的顶点哪些可以合并,
倒数第二层中
第一个 * 的左边是a、右边是b,
第二个 * 的左边是a、右边是b,
第三个 * 的左边是a、右边是b,
所以第一、二、三个 * 可以合并,如下图:

如上图,此时倒数第二层中存储运算符的顶点全部合并完毕,继续判断倒数第三层中存储运算符的顶点哪些可以合并,
倒数第三层中
第一个 * 的左边是(a * b)、右边是(a * b),
第二个 * 的左边是(a * b)、右边是c,
所以第一个 * 和第二个 * 不能合并,
如上图,此时倒数第三层中存储运算符的顶点全部合并完毕,
由于倒数第四层中存储运算符的顶点都只有一个,所以一定不需要合并,因为合并至少需要两个顶点,
至此,就得到了一个最简的用有向无环图表示的算术表达式。
