高等数学-积分
一、不定积分
定理:如果函数f(x)在区间I上连续,那么f(x)在区间I上一定有原函数,即一定存在区间I上的可导函数F(x),使得F'(x)=f(x) ,x∈I
简单地说:连续函数必有原函数。



极限lim*0->x {[∫*0^x sin(t^2)dt]/x^3}=1/3
变上限积分∫*π/2^x (sint/t)'dt=(sinx)/x-π/2
注:(1)若等式两边函数相等(自变量都是x),则等号两边同时求不定积分,等号仍成立。
例:
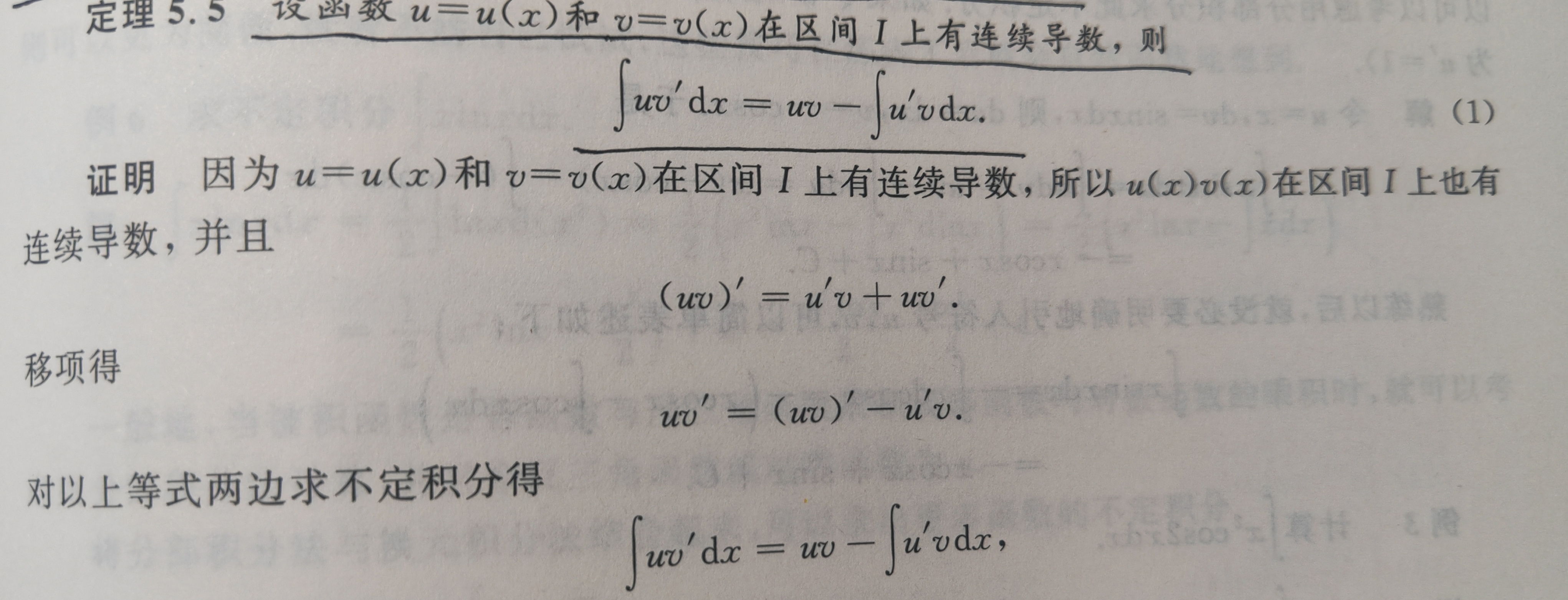
(2)积分是逆转求导:∫(dy/dx) dx=y
二、定积分
(1)可积的两个充分条件:
定理1:设函数f(x)在区间[a,b]上连续,则f(x)在[a,b]上可积。
定理2:设函数f(x)在区间[a,b]上有界,并且只有有限个间断点,则f(x)在[a,b]上可积。
如不作特别的说明,往后总假定所讨论的定积分是存在的。
(2)定积分的基本性质

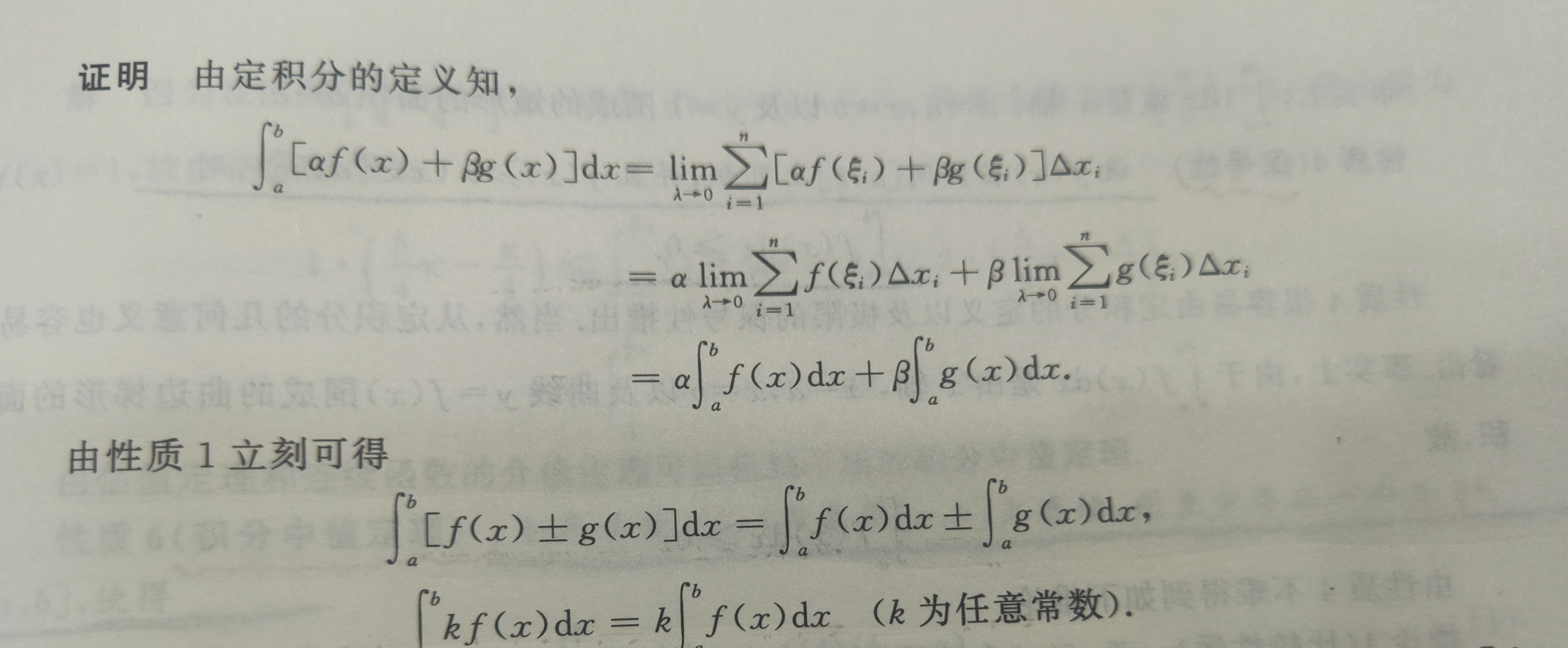




 (3)定积分的换元法与分部积分法
(3)定积分的换元法与分部积分法
a.换元法

该定理告诉我们:在一定条件下,dx可以作为微分记号来对待,即应用换元公式(1)时,如果将积分变量x换为φ(x),则dx就换成φ'(t)dt,这正好是函数x=φ(t)的微分
注:
1)换元必换限,上限对上限,下限对下限,即如果用x=φ(t)把原来的变量换成了新变量t,积分限也必须换成新变量t的积分限,并且原来下限对应的参数做下限,原来上限对应的参数做上限。
2)不要求x=φ(t)单调,从而其反函数也可以不存在。
b.分部积分法

例1:
1/3y^3*e^(-y^2)求原函数?

例2:
-2∫*0^2π asin2a da=acos2a |*0^2π-∫*0^2π cos2a da
三、微积分基本公式
(1)变上限积分

变上限积分求导证明??
(2)微积分学基本公式(牛莱公式):
设函数f(x)在区间[a,b]上连续,F(x)是f(x)在[a,b]上的一个原函数,则∫*a^b f(x)dx=F(b)-F(a).
证明:由已知及2中的定理,函数F(x)和Φ(x)=∫*a^x f(t)dt都是函数f(x)在区间[a,b]上的原函数,从而F(x)-Φ(x)=C(x∈[a,b]),其中C为一个常数。
令x=a得F(a)-Φ(a)=C.又由于Φ(a)=0,所以C=F(a),代入上式得Φ(x)=F(x)-F(a)(x∈[a,b]),即∫*a^x f(t)dt=F(x)-F(a)(x∈[a,b]).特别地,当x=b时,即有∫*a^b f(x)dx=F(b)-F(a).
该公式又可以写成:
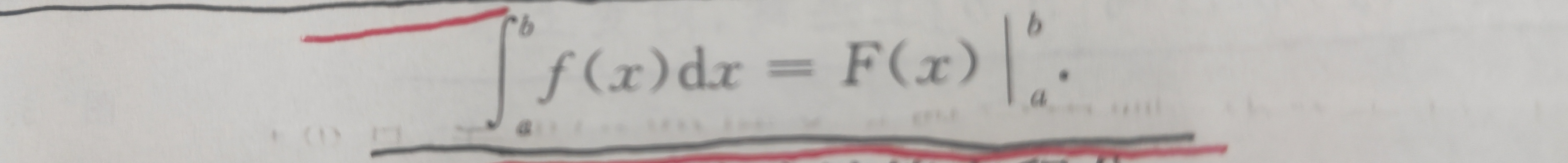
这个公式告诉我们:要计算连续函数f(x)的定积分
,只需先求出f(x)的任何一个原函数F(x),然后将F(x)在积分上限的值减去F(x)在积分下限的值即可。
四、求定积分
1)∫*0^π/2 (sinx)^2cosxdx=∫0^π/2 (sinx)^2dsinx=1/3(sinx)^3 |0^π/2=1/3
2)∫*0^1/2 dx/[√x(1-x)]=∫*0^1/2 [1/√(1-x)*]·1/√xdx=2∫*0^1/2 d(√x)/[1-(√x)^2]=2arcsin(√x) |*0^1/2=2arcsin(√2/2)=π/2
五、二重积分
(1)二重积分的性质:


例1:
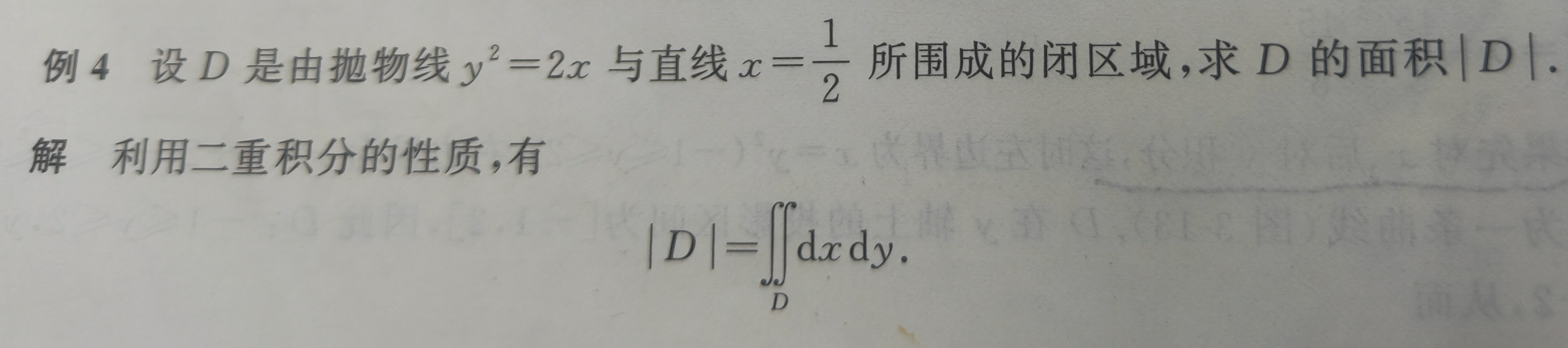

 例2:
例2:
利用二重积分计算下面图形的面积:由抛物线y^=2x与直线y=x-4所围成的平面图形。
解:
解方程组得到抛物线y^=2x与直线y=x-4的两个交点为(2,-2),(8,4)
先对x、后对y积分:
被积区域:-2
平面图形的面积:∫∫1dxdy=∫*-2^4 dy∫*(y^2)/2^(y+4) dx=∫*-2^4 [(y+4)-(y^2)/2]dy=18
当被积函数f(x,y)=1时,计算二重积分就相当于计算被积区域的面积
(2)极坐标
一般来说,当积分区域D为圆形、扇形、或环形闭区域时,而被积函数含有x^2+y^2或者arctan(y/x)等式子时,用极坐标计算二重积分往往比较简单。

注:[(sina)^3]'=1/3[cosa)^3]-cosa
结论:(1)∫0->+∞* e^[-x^2]dx=(√π)/2
(2)∫-∞->+∞* e^[-x^2]dx=√π
六、三重积分
(1)对称奇偶性

(2)三重积分的计算

(3)[d(e^-∫P(x)dx)]/dx=-P(x)e^-∫P(x)dx
