非线性1 修改

第一章为读者介绍了非线性动力学与混沌理论的基本概念、发展历史以及应用领域。

1.1 动力学简史：

• 从牛顿力学开始，介绍动力学作为物理学分支的发展历程。
• 重点介绍了庞加莱对混沌现象的早期探索，以及20世纪60年代洛伦兹方程的发现，标志着混沌理论的诞生，并回顾了20世纪70年代混沌理论的快速发展。
• 洛伦兹发现了混沌的特定结构：
  

1.2 非线性的重要性：

• 消除时间依赖：增加一个维度

• 
  $x^{\prime \prime }\to x_1,x^{\prime }\to x_2,t\to x_3$
  

• 强调非线性系统难以求解：因为叠加原理失效

• 但几何方法可以帮助我们理解其定性特征。

• 相空间：
  

第二章 直线上的流

2.1 几何的思维方式：

• 系统x’ = sin(x)，解：
  
  在x轴上表示出x的速度向量：
  向量场
  
  $x\in (\pi /4,\pi )$:x-t图
  

• 不动点的概念:$\dot{x}=0$，表示没有流动

• 区分稳定不动点（吸引子、汇）和不稳定不动点（排斥子、源）：
  在这里，实轴就是相空间

2.2 不动点与稳定性：

• 相点：放置在初始条件$x_0$的粒子
• 轨迹：相点随时间根据X（t）运动
• 相图的概念：所有不同的定性轨迹
  
  2.3 种群增长：
  公式：

• 图像：

N<K增加，且先慢后快后慢

2.4 线性稳定性分析：

• 线性稳定性分析：判断不动点x*的稳定性

• 给一个小扰动$\eta$:$\eta (t)=x(t)-x^{\ast }$
  
  在不动点处，$\dot{x}=f(x^{\ast })=0$,要观察一段时间后这个扰动是变大还是变小
  
  线性化：
  得到$\dot{\eta }\approx \eta$ $f^{\prime }(x^{\ast })$

  最终$\eta =e^{f^{\prime }(x^{\ast })+C}$，指数律增减

• 判断不动点的稳定性：不动点处的斜率f’(x*)

• 斜率>0:不稳定，

• 斜率<0:稳定，

• 斜率=0：不能忽略O(η²)

• 特征时间尺度：1/f’(x*)：x(t)在t时间发生较大变化所需的时间

2.5 存在性与唯一性：

• 存在性与唯一性定理：

2.6 振动的不可能性：

• 一维自治系统中振动现象的不可能性：$\dot{x}=f(x)$无周期解
  *一个点不可能有两个速度

2.7 势：

• 将一阶系统$\dot{x}=f(x)$可视化
• 势的概念：$f(x)=-\frac{dV}{dx}$
• 与向量场之间的关系:两边对x求导：f’=-V’’
• V的局部最小值=>稳定不动点，局部最大值=>不稳定
• 实例：$\dot{x}=-x$
  $dV/dx=x^2/2+C$

2.8 利用计算机解方程：

• 显式欧拉法

• 改进欧拉法

• 龙格库塔法（四阶）

• 

第三章——分岔。

分岔是指当参数变化时，系统的动力学行为发生定性改变的过程：
例如不动点的出现、消失或稳定性改变。
3.1 鞍-结分岔：

• 标准形式：$x^{\prime }=r+x^2$:
  r-x图
  
  变体：$\dot{x}=r-x-e^{-x}$
  标准形式：$\dot{x}=r\pm x^2$

3.2 跨临界分岔

• 定义：跨临界分岔是指不动点的稳定性发生改变，但不动点本身不消失的现象。
• 标准形式：$x^{\prime }=rx-x^2$
• 稳定性的交换：
  分叉曲线：
  
• 变体：$\dot{x}=r\ln x+x-1$在x=1附近的分岔：
• 变换：u=x-1

3.3 激光阈值

• 激光阈值的物理机制:当泵浦强度超过阈值时，系统会发生跨临界分岔，从而产生激光。

• 
  
  分岔图：N0=k/G处发生跨临界分叉

• $N_0/G$为激光阈值

3.4 叉式分岔

• 叉式分岔是指具有对称性的系统，其不动点成对出现或消失的现象。
• 超临界叉式分岔和亚临界叉式分岔：分别对应着不动点在分岔后不消失和消失的情况。
• 

• 3.4.1 超临界叉式分岔

• 标准形式：$x^{\prime }=rx-x^3$

• 当变换$x\to -x$时，方程不变——向量场等变/对称

• 向量场：
  分岔图：
  

• 变体：$\dot{x}=-x+\beta \tanh x$

• 向量场：

• 

• 分岔图：$\beta =\tanh x/x$
  

• 3.4.2亚临界叉式分岔

• 一个示例： $x^{\prime }=rx+x^3$

• 分岔图：
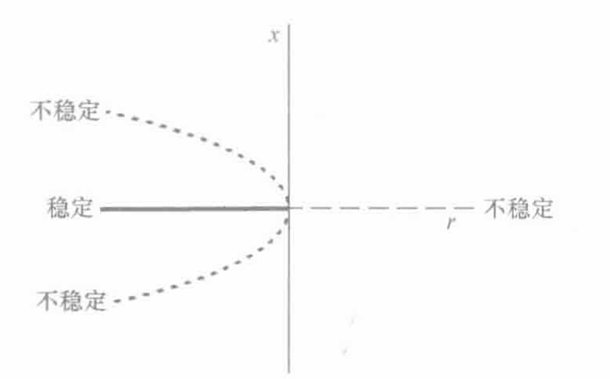
  上述系统容易产生爆炸：即有限时间内x(t)->无穷
  标准形式$x^{\prime }=rx+x^3-x^5$（为了对称，不能加x^4）

• 跳跃：r=0时，跳跃到大振幅分支

• 滞后：减小r也不能回到原点了，除非减小到r_s
  

3.5 旋转环上的过阻尼球

• 介绍了旋转环上的过阻尼球问题，并建立了一个简化的模型，解释了小球在旋转环上的运动。
• 
  

顶部：φ=π，底部：=0

• 发现当旋转环的角速度超过某个临界值时，系统会发生超临界叉式分岔，从而出现三个平衡点。
• 无量纲化、无量纲组：

3.6 不完美分岔与灾变

• 定义：不完美分岔是指当存在对称性的近似时，系统会发生分岔的现象。
• 灾变：当参数变化时，系统状态会跨越某个临界值，之后发生不连续的改变。
• 标准形式：x’ = r - x^3 + x
• 分析方法：通过观察函数 f(x) 和 x 轴的交点，以及它们在分岔点附近的泰勒展开式，可以判断分岔的发生和不动点的稳定性。
• 应用：昆虫爆发、斜线上的小球等。
  3.7 昆虫爆发
• 介绍了云杉蚜虫爆发模型，解释了蚜虫数目突然增加的现象。
• 通过无量纲分析，将模型简化为一维系统，并分析其不动点的分岔行为。
• 发现当天敌捕食作用增强时，系统会发生鞍-结分岔，从而导致蚜虫爆发。
• 该模型展示了分岔在生态学中的应用，以及如何通过参数变化来预测系统的行为。
  本章通过多种类型的分岔，以及它们在科学和工程中的应用，展示了分岔的多样性和重要性。分岔是理解非线性系统行为的关键，它在物理学、生物学、工程学等多个领域都有着广泛的应用。

3.2 跨临界分岔：

• 介绍跨临界分岔的概念，并以x’ = r(1 - x)为例，说明其发生机制和特征。
• 解释跨临界分岔的标准形式，并介绍其绘图方法。
• 通过实例，说明跨临界分岔在激光物理中的应用。
  3.3 激光阈值：
• 介绍激光物理背景，并介绍一个简化激光模型。
• 利用向量场和相图，分析激光阈值现象，并解释其物理意义。
• 讨论该模型的局限性，并引出更复杂的激光模型。
  3.4 叉式分岔：
• 介绍叉式分岔的概念，并区分超临界叉式分岔和亚临界叉式分岔。
• 以x’ = r - x^3为例，说明超临界叉式分岔的发生机制和特征。
• 解释超临界叉式分岔的标准形式，并介绍其绘图方法。
• 通过实例，说明叉式分岔在物理和生物学中的应用。
  3.5 旋转环上的过阻尼球：
• 介绍旋转环上过阻尼球的问题，并推导其动力学方程。
• 利用向量场和相图，分析过阻尼球在不同参数下的运动状态。
• 引入量纲分析和尺度化的概念，解释将二阶系统近似为一阶系统的可行性。
• 讨论该问题的奇异极限性质，并引出奇异摄动理论。
  3.6 不完美分岔与灾变：
• 介绍不完美分岔的概念，并以x’ = y^3 - xy为例，说明其发生机制和特征。
• 解释尖点灾变的概念，并介绍其绘图方法。
• 通过实例，说明不完美分岔和尖点灾变在力学和生物学中的应用。
  3.7 昆虫爆发：
• 介绍云杉蚜虫爆发模型，并解释其物理背景和参数含义。
• 利用向量场和相图，分析蚜虫数目随时间变化的动力学特征。
• 讨论模型的近似方法和参数估计，并解释爆发现象的物理意义。
  3.8 本章总结：
• 本章深入探讨了分岔现象，并介绍其在科学中的应用。
• 介绍了鞍-结分岔、跨临界分岔、叉式分岔等不同类型的分岔，并解释其发生机制和特征。
• 通过实例，展示了分岔现象在物理、生物学等领域的应用，并说明其对理解自然界复杂现象的重要性。
  第三章的核心观点在于：
• 分岔是描述系统行为随参数变化而发生定性改变的关键概念。
• 分岔现象在自然界中普遍存在，并具有重要的科学意义。
• 几何方法可以帮助我们直观地理解分岔现象，并预测其发生规律。
• 分岔现象在多个领域具有广泛的应用，例如激光物理、力学、生物学等。