872. 最大公约数(史上最详细讲解 7种算法,STL+算法标准实现)
一,什么是最大公约数
最大公约数(Greatest Common Divisor)指两个或多个整数共有约数中最大的一个。也称最大公因数、最大公因子,a, b的最大公约数记为(a,b),同样的,a,b,c的最大 公约数记为(a,b,c),多个 整数的最大公约数也有同样的记号。求最大公约数有多种 方法,常见的有 质因数分解法、 短除法、 辗转相除法、 更相减损法。
二,辗转相减法求最大公约数(又称更相损减术)
用(a,b)表示a和b的最大公因数:有结论(a,b)=(a,k*a+b),其中a、b、k都为自然数。
也就是说,两个数的最大公约数,将其中一个数加到另一个数上,得到的新数,其公约数不变,比如(4,6)=(4+6,6)=(4,6+2×4)=2.
要证明这个原理很容易:如果p是a和k*a+b的公约数,p整除a,也能整除k*a+b.那么就必定要整除b,所以p又是a和b的公约数,从而证明他们的最大公约数也是相等的.
基于上面的原理,就能实现我们的迭代相减法:(78,14)=(64,14)=(50,14)=(36,14)=(22,14)=(8,14)=(8,6)=(2,6)=(2,4)=(2,2)=(0,2)=2
基本上思路就是大数减去小数,一直减到能算出来为止,在作为练习的时候,往往进行到某一步就已经可以看出得值.
更相减损法出自《九章算术》:“可半者半之,不可半者,副置分母、子之数,以少减多,更相减损,求其等也。以等数约之。”
具体方法为两个数之间大的数字减小的数字,之后将得到的差作为减数,较小的数作为被减数,再次相减,直到与所得的差相同,此时的差即为两个数之间的最大公约数。
代码:
int gcd2(int a, int b)
{
while(a != b)
if(a > b) a -= b;
else b -= a;
return a;
}四,辗转相减到辗转相除
迭代相减法简单,不过步数比较多,实际上我们可以看到,在上面的过程中,由(78,14)到(8,14)完全可以一步到位,因为(78,14)=(14×5+8,14)=(8,14),由此就诞生出我们的辗转相除法.
即:(a, b) = (a % b, b) = (b, a %b)
相当于每一步都把数字进行缩小,等式右边就是每一步对应的缩小结果。
对(a, b)连续使用辗转相除,直到小括号内右边数字为0,小括号内左边的数就是两数最大公约数。
时间复杂度:O(log n)(以2为底)
附,证明图: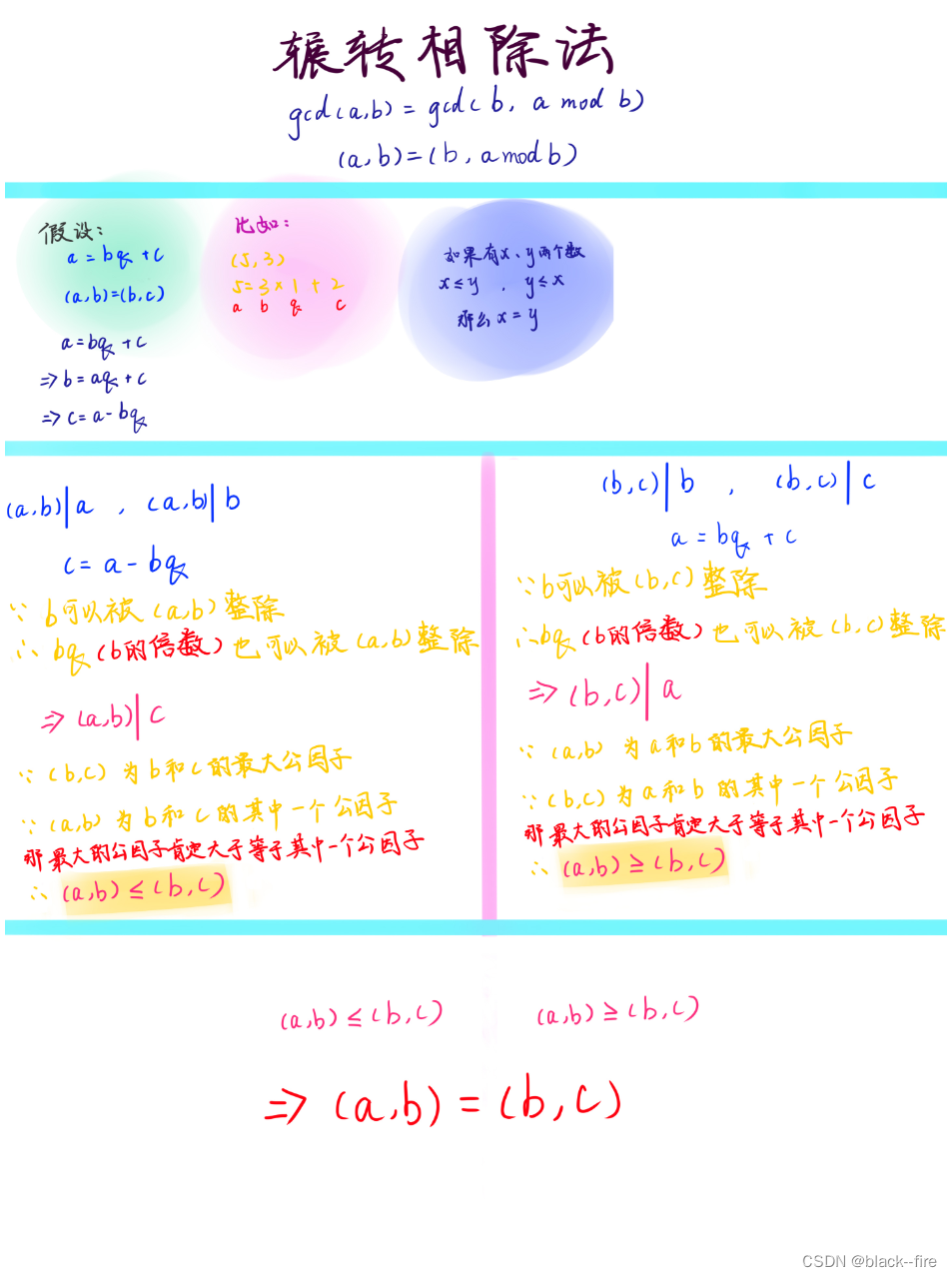
代码:
#include <bits/stdc++.h>
using namespace std;
long long n,a,b;
int ggcd(int n,int m)
{
return (n == 0) ? m : f((m % n),n);
}
int main()
{
cin>>n;
while(n--)
{
cin>>a>>b;
cout<<ggcd(a,b)<<endl;
}
return 0;
}五,STL
1.__gcd(a,b)
库algorithm
在库algorithm中提供了求最大公约数的方法,这是目前我所找到的最快的算法,没有之一。具体使用方法是__gcd(a, b) 即返回了ab的最大公约数,需要注意的是gcd前面有两个下划线。
代码:
#include<iostream>
#include<algorithm>
using namespace std;
int main()
{
int t;
cin >> t;
while(t--){
int a, b;
cin >> a >> b;
cout << __gcd(a, b);
}
}=========================================================================
2.gcd(a.b)
在库numeric中提供了求最大公约数的方法,这是我提供的几种算法中最慢的,仅作扩展,如无必要,不要使用。使用方法直接就是gcd(a, b)。因此我建议各位在标记函数名称时,与此区别开来。
代码:
#include<iostream>
#include<numeric>
using namespace std;
int main()
{
int t;
cin >> t;
while(t--){
int a, b;
cin >> a >> b;
cout << gcd(a, b);
}
}六,位运算
利用位运算的特性,将两数交换改成位运算。
inline可加可不加。我实际试验中,在1e8次执行后,加与不加的时间差在80ms左右,而两者本来的运行时间均在3000ms上下,即差别不大
代码:
inline int gcd3(int a, int b)
{
while(b ^= a ^= b ^= a %= b);
return a;
}七,超快算法
利用取模特点,几乎与algorithm的时间一致
代码:
int gcd4(int a, int b){//超快
if(!a || !b)
return max(a, b);
for(int t; t = a % b; a = b, b = t);
return b;
}讲了那么多,如果听懂了的话请点个赞再走吧QAQ
