多因子线性回归实战
线性回归理论知识
通俗统计学原理入门27 线性相关 线性相关系数 协方差 简单一元线性回归_哔哩哔哩_bilibili
https://www.bilibili.com/video/BV1ACmpYfENu?spm_id_from=333.788.videopod.sections&vd_source=65d7800c55c288725af7f82cd2d0e8de
任务
线性回归预测房价:9.9 多因子线性回归实战_哔哩哔哩_bilibili
基于 usa_housing_price.csv 数据,建立线性回归模型,预测合理房价:
1、以面积为输入变量,建立单因子模型,评估模型表现,可视化线性回归预测结果
2、以 income、house age、numbers of rooms、population、area 为输入变量,建立多因子模型,评估模型表现
3、预测 Income=65000,House Age=5,Number of Rooms=5,Population=30000,size=200 的合理房价
数据
usa_housing_price.csv
百度搜索 “usa_housing_price.csv下载” 可以下载到。https://www.bilibili.com/video/BV1ACmpYfENu?spm_id_from=333.788.videopod.sections&vd_source=65d7800c55c288725af7f82cd2d0e8de
代码
# load the data
import pandas as pd
import numpy as np
data = pd.read_csv('usa_housing_price.csv')
data.head()
数据探查
# # 数据探查:可视化
%matplotlib inline
from matplotlib import pyplot as plt
fig = plt.figure(figsize = (10,10))
# 收入 与 价格 散点图
fig1 = plt.subplot(231) # 2 行 3 列的图形,画第 1 副图
plt.scatter(data.loc[:,'Avg. Area Income'], data.loc[:,'Price']) # x = ‘Avg.Area Income’ 列 ,y = 'Price'列
plt.title('Price VS Income')# 房屋年龄 与 价格 散点图
fig2 = plt.subplot(232) # 2 行 3 列的图形,画第 2 副图
plt.scatter(data.loc[:,'Avg. Area House Age'], data.loc[:,'Price']) # x = ‘Avg.Area Income’ 列 ,y = 'Price'列
plt.title('Price VS House Age')# 房间个数 与 价格 散点图
fig3 = plt.subplot(233) # 2 行 3 列的图形,画第 3 副图
plt.scatter(data.loc[:,'Avg. Area Number of Rooms'], data.loc[:,'Price']) # x = ‘Avg.Area Income’ 列 ,y = 'Price'列
plt.title('Price VS Number of Rooms')# 人口数量 与 价格 散点图
fig4 = plt.subplot(234) # 2 行 3 列的图形,画第 4 副图
plt.scatter(data.loc[:,'Area Population'], data.loc[:,'Price']) # x = ‘Avg.Area Income’ 列 ,y = 'Price'列
plt.title('Price VS Area Populations')# 面积 与 价格 散点图
fig5 = plt.subplot(235) # 2 行 3 列的图形,画第 5 副图
plt.scatter(data.loc[:,'size'], data.loc[:,'Price']) # x = ‘Avg.Area Income’ 列 ,y = 'Price'列
plt.title('Price VS size')plt.show()
任务1、以面积为输入变量,建立单因子模型,评估模型表现,可视化线性回归预测结果
#任务1、以面积为输入变量,建立单因子模型,评估模型表现,可视化线性回归预测结果
#define X and Y
X = data.loc[:,'size']
y = data.loc[:,'Price']
# X.head()
# y.head()#模型训练需要二维数据,所以要进维度转换
X = np.array(X).reshape(-1,1) # 对X进行维度转换
print(X.shape)# set up the linear regression model
from sklearn.linear_model import LinearRegression
LR1 = LinearRegression() # 使用默认参数创建模型
# train the model
LR1.fit(X, y) # LinearRegression(copy_X=True, fit_intercept=True, n_jobs=None, normalize=False)# calculate the price vs size
y_predict_1 = LR1.predict(X) # 进行预测
print(y_predict_1)# evaluate the model
from sklearn.metrics import mean_squared_error, r2_score
mean_squared_error_1 = mean_squared_error(y,y_pridict_1) # 两个参数:y 实际值 、y 预测值
r2_score_1 = r2_score(y,y_pridict_1)
print(mean_squared_error_1, r2_score_1) # 108771672553.6264 0.1275031240418234
# R2 分数越接近 1 越好#把图画出来看
fig6 = plt.figure(figsize = (8,5))
plt.scatter(X,y) # 把原始数据画出来
plt.plot(X,y_predict_1,'r')#把这条回归直线也画出来
plt.show()
# 从图形可以看出,面积 和价格的关系图中,价格范围很广,也就是说,价格可能跟面积以外的其它因素有有关系
任务2、以 income、house age、numbers of rooms、population、area 为输入变量,建立多因子模型,评估模型表现
# 任务2、以 income、house age、numbers of rooms、population、area 为输入变量,建立多因子模型,评估模型表现
# define X_multi
X_multi = data.drop(['Price'], axis =1) # dataframe 去掉某列
X_multi.head()
# set up 2nd linear model
LR_multi = LinearRegression()
#train the model
LR_multi.fit(X_multi,y) #模型训练# make prediction
y_predict_multi = LR_multi.predict(X_multi)
print(y_predict_multi) # 看不出预测的好不好#模型评估
mean_squared_error_multi = mean_squared_error(y,y_predict_multi) # 两个参数:y 实际值 、y 预测值
r2_score_multi = r2_score(y, y_predict_multi)
print(mean_squared_error_multi, r2_score_multi) # r2_score_multi=0.9180229195220739, 与 1 很接近了
#上面单因子里 r2_score_1 = 0.1275031240418234#可视化
fig7 = plt.figure(figsize=(8,5))
plt.scatter(y,y_predict_multi) # 把实际y 值 和 预测 y 值画成 散点图,如果能集中在一条直线上,说明模型还不错
plt.show() # 从下图可以看出,集中度还是不错的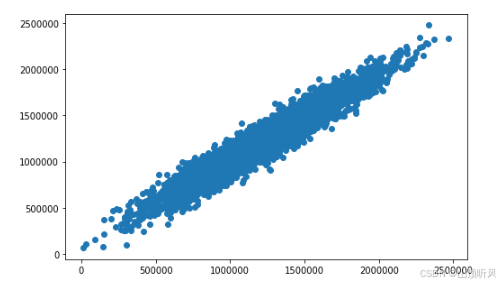
#展示单因子图,与上面多因子图进行对比
fig8 = plt.figure(figsize = (8,5))
plt.scatter(y, y_predict_1)
plt.show() # 通过对比可以看出,多因子的图集中度比下面单因子的要好很多,单因子很离散(预测值和实际值差很多)
任务3、预测 Income=65000,House Age=5,Number of Rooms=5,Population=30000,size=200 的合理房价
#任务3、预测 Income=65000,House Age=5,Number of Rooms=5,Population=30000,size=200 的合理房价
X_test = [65000,5,5,30000,200]
X_test = np.array(X_test).reshape(1,-1)
print(X_test) # [[65000 5 5 30000 200]]y_test_predict = LR_multi.predict(X_test)
print(y_test_predict) # [817052.19516298]线性回归房价实战 summary
通过搭建线性回归模型,实现单因子的房屋价格预测;
在单因子模型效果不好的情况下,通过考虑更多的因子,建立了多因子模型;
多因子模型达到了更好的预测效果,r2 分数为 0.91;
实现了预测结果的可视化,直观对比预测价格与实际价格的差异。
