动态规划之完全背包问题

牛客网例题为例,由于 leetcode没有经典例题可以讲解,牛客网这道可以当作模板题
题目分析
如果看过我的01背包分析,完全背包就是物品可以选无数多个
算法原理(第一小问)
第一小问就是不必装满(也就是可以装满也可以不装满)
1.状态表示:dp[i][j]:从前i个物品中,总体积不超过j的所有选法中,最大的价值
2.状态转移方程:

i位置的商品可分为不选/选1个/选2个/选3个等等
所以我们可以发现状态转移方程无非就是01背包问题的基础上可以选多个
但是这里发现选一个选两个选三个就是重复的有规律的,那我们就想能不能用一个状态去表示
优化
1.数学等价代换

首先我们根据状态转移方程写出最终的状态方程
我们发现i-1是不变的,j会变
所以我们尝试列出dp[i][j-v[i]]的状态转移方程
发现dp[i][j-v[i]+w[i]=dp[i][j]的后面的一大坨,此时就可以等价代换
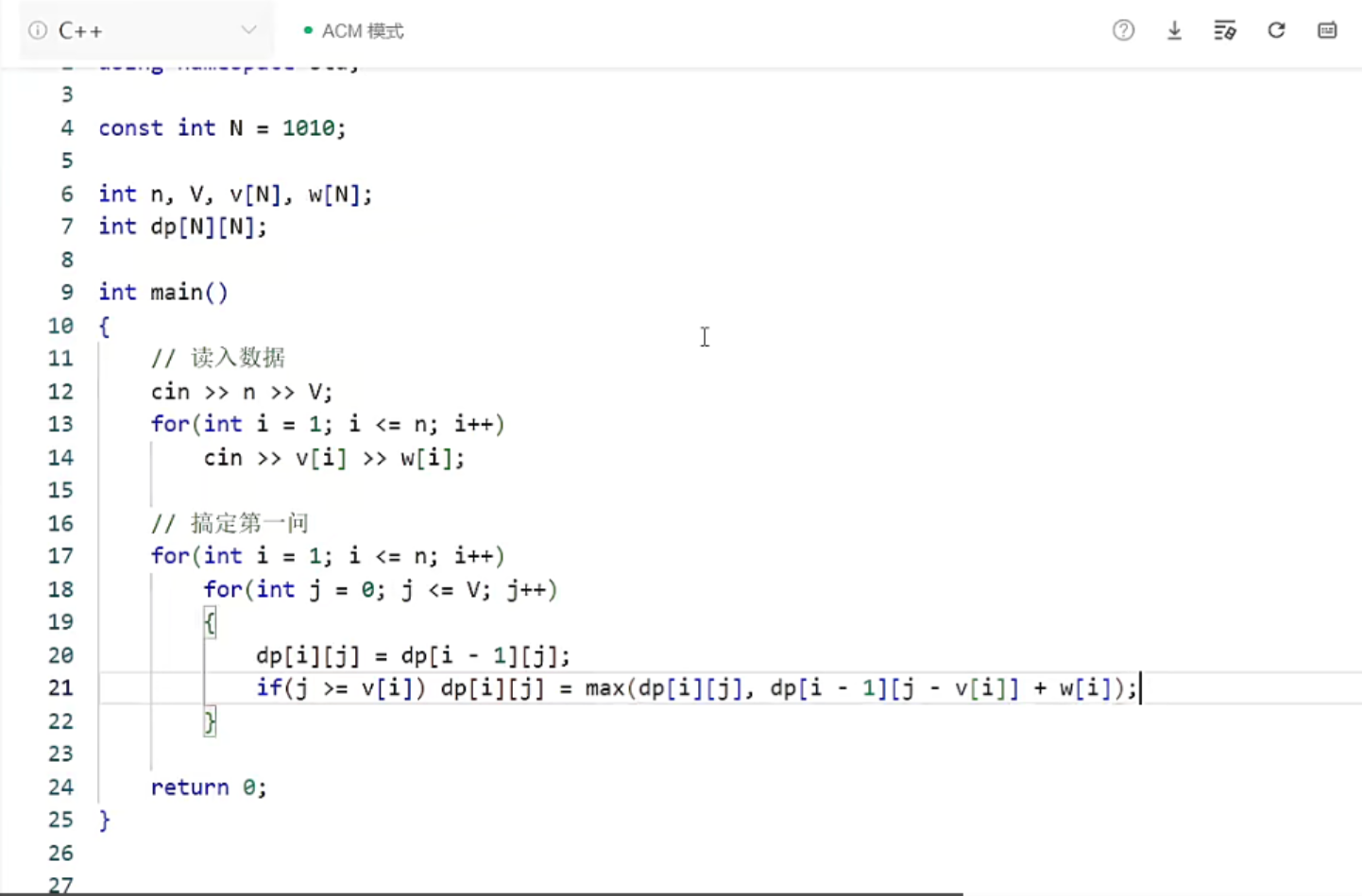
所以最后的dp[i][j]=max(dp[i-1][j],dp[i][j-v[i]]+w[i]);标红的是等价代换的
但是我们这里的j-[v[i]]可能不存在,所以我们在写代码的时候要先判断一下
初始化
为什么第一列不用初始化?
因为我们在用dp【i】【j-v【i】】的时候是会先判断的
也就是j-v[i]>=0,才会用,如果是一列,j=0,只有v[i]=0才会进入,那你的dp[i][j-v[i]]=dp[i][0]
根本不会越界
第一行的初始化就是你没有商品的时候能不能凑出0/1/2/3的体积,显然不能,所以初始化为0
注意:填表的时候要清楚下标的映射关系
填表顺序

发现我们填某个位置的时候需要用到上一行和这一行左边的
所以我们填表要从上往下,从左往右
返回值
dp[n][v]
算法原理(第二小问)
第一小问是不必装满
第二小问是必须装满

绿色代表新的状态表示:简单修改总体积正好等于j就行

因为你的状态是总体积刚好等于j,你要判断你这次加上这个能不能刚好等于j,所以你在找前面的时候你要判断前面是否能选出来j-v[i]的体积
我们这里用-1表示前面凑不出来总体积,为什么不用0
第一,你要想用0这个状态表示什么,是表示凑不出来,还是表示所有选法中最大的价值
第二,你如果用0去表示前面凑不出来,那max求dp[i][j-v[i]]+w[i]可能就会选到,
但你前面都凑不出来,你又把这一项选上了,这会导致全部的填表都是错误的
所以我们用-1来表示前面凑不出来
我们需要判断if(j-v[i]>=0&&dp[i][j-v[i]]!=-1)
红色表示前面有这个体积,绿色表示前面能凑出来,在+上i物品的体积就刚刚好

第一列也不用初始化,和上面一样
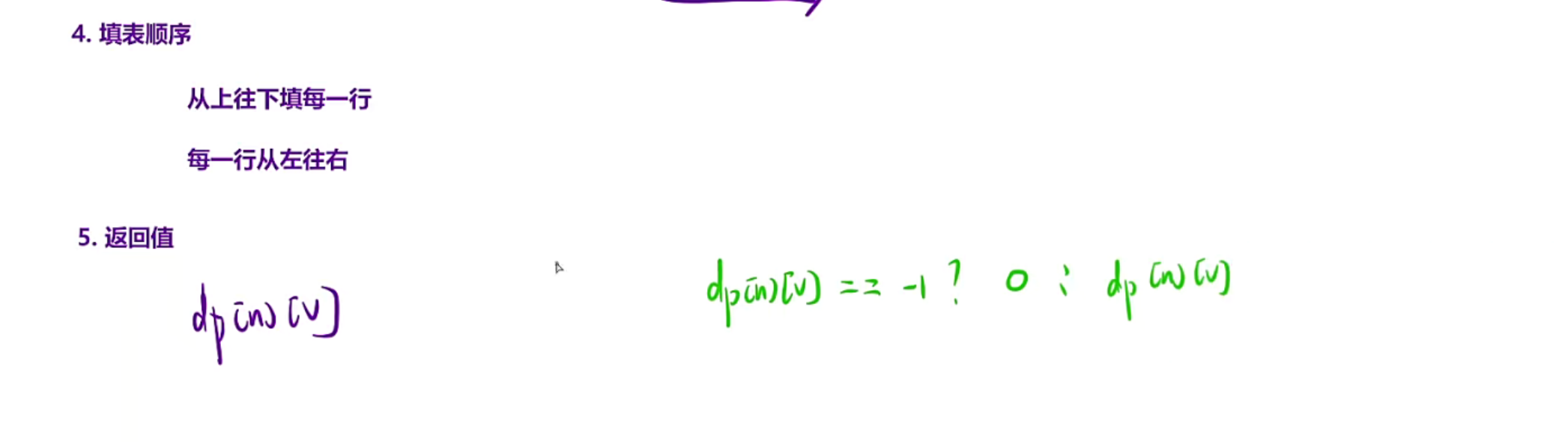
代码编写