[特征工程]机器学习-part2

1 特征工程概念

特征工程:就是对特征进行相关的处理

一般使用pandas来进行数据清洗和数据处理、使用sklearn来进行特征工程

特征工程是将任意数据(如文本或图像)转换为可用于机器学习的数字特征,比如:字典特征提取(特征离散化)、文本特征提取、图像特征提取。

特征工程步骤为：

• 特征提取， 如果不是像dataframe那样的数据，要进行特征提取，比如字典特征提取，文本特征提取

• 无量纲化(预处理)

  • 归一化

  • 标准化

• 降维

  • 底方差过滤特征选择

  • 主成分分析-PCA降维

2 特征工程API

• 实例化转换器对象，转换器类有很多，都是Transformer的子类, 常用的子类有:

  DictVectorizer      字典特征提取
  CountVectorizer     文本特征提取
  TfidfVectorizer     TF-IDF文本特征词的重要程度特征提取 
  MinMaxScaler        归一化
  StandardScaler      标准化
  VarianceThreshold   底方差过滤降维
  PCA                 主成分分析降维

• 转换器对象调用fit_transform()进行转换, 其中fit用于计算数据，transform进行最终转换

  fit_transform()可以使用fit()和transform()代替

  data_new = transfer.fit_transform(data)
  可写成
  transfer.fit(data)
  data_new = transfer.transform(data)

3 DictVectorizer 字典列表特征提取

稀疏矩阵

稀疏矩阵是指一个矩阵中大部分元素为零，只有少数元素是非零的矩阵。在数学和计算机科学中，当一个矩阵的非零元素数量远小于总的元素数量，且非零元素分布没有明显的规律时，这样的矩阵就被认为是稀疏矩阵。例如，在一个1000 x 1000的矩阵中，如果只有1000个非零元素，那么这个矩阵就是稀疏的。

由于稀疏矩阵中零元素非常多，存储和处理稀疏矩阵时，通常会采用特殊的存储格式，以节省内存空间并提高计算效率。

三元组表 (Coordinate List, COO)：三元组表就是一种稀疏矩阵类型数据,存储非零元素的行索引、列索引和值:

(行,列) 数据

(0,0) 10

(0,1) 20

(2,0) 90

(2,20) 8

(8,0) 70

表示除了列出的有值, 其余全是0

from sklearn.feature_extraction import DictVectorizerdata = [{'city':'北京','temperature':100},{'city':'上海','temperature':60},{'city':'深圳','temperature':30}]
# 创建一个字典列表特征提取工具
tool = DictVectorizer(sparse=False)
# 字典列表特征提取
data = tool.fit_transform(data)
print(data)
print(tool.feature_names_)

非稀疏矩阵（稠密矩阵）

非稀疏矩阵，或称稠密矩阵，是指矩阵中非零元素的数量与总元素数量相比接近或相等，也就是说矩阵中的大部分元素都是非零的。在这种情况下，矩阵的存储通常采用标准的二维数组形式，因为非零元素密集分布，不需要特殊的压缩或优化存储策略。

• 存储：稀疏矩阵使用特定的存储格式来节省空间，而稠密矩阵使用常规的数组存储所有元素，无论其是否为零。

• 计算：稀疏矩阵在进行计算时可以利用零元素的特性跳过不必要的计算，从而提高效率。而稠密矩阵在计算时需要处理所有元素，包括零元素。

• 应用领域：稀疏矩阵常见于大规模数据分析、图形学、自然语言处理、机器学习等领域，而稠密矩阵在数学计算、线性代数等通用计算领域更为常见。

在实际应用中，选择使用稀疏矩阵还是稠密矩阵取决于具体的问题场景和数据特性。

(1) api

• 创建转换器对象:

  sklearn.feature_extraction.DictVectorizer(sparse=True)

  参数:

  sparse=True返回类型为csr_matrix的稀疏矩阵

  sparse=False表示返回的是数组,数组可以调用.toarray()方法将稀疏矩阵转换为数组

• 转换器对象:

  转换器对象调用fit_transform(data)函数，参数data为一维字典数组或一维字典列表,返回转化后的矩阵或数组

  转换器对象get_feature_names_out()方法获取特征名

(2)示例1 提取为稀疏矩阵对应的数组

from sklearn.feature_extraction import DictVectorizer
data = [{'city':'成都', 'age':30, 'temperature':200}, {'city':'重庆','age':33, 'temperature':60}, {'city':'北京', 'age':42, 'temperature':80}]
#创建DictVectorizer对象
transfer = DictVectorizer(sparse=False)
data_new = transfer.fit_transform(data)
# data_new的类型为ndarray
#特征数据
print("data_new:\n", data_new)
#特征名字 
print("特征名字：\n", transfer.get_feature_names_out())

data_new:[[ 30.   0.   1.   0. 200.][ 33.   0.   0.   1.  60.][ 42.   1.   0.   0.  80.]]
特征名字：['age' 'city=北京' 'city=成都' 'city=重庆' 'temperature']

import pandas
pandas.DataFrame(data_new, columns=transfer.get_feature_names_out())

(3)示例2 提取为稀疏矩阵

from sklearn.feature_extraction import DictVectorizer
data = [{'city':'成都', 'age':30, 'temperature':200}, {'city':'重庆','age':33, 'temperature':60}, {'city':'北京', 'age':42, 'temperature':80}]
#创建DictVectorizer对象
transfer = DictVectorizer(sparse=True)
data_new = transfer.fit_transform(data)
#data_new的类型为<class 'scipy.sparse._csr.csr_matrix'>
print("data_new:\n", data_new)
#得到特征 
print("特征名字：\n", transfer.get_feature_names_out())

其中(row,col)数据中的col表示特征， 本示例中0表示 ‘age’, 1表示‘city=北京’,……

data_new:(0, 0)    30.0(0, 2)    1.0(0, 4)    200.0(1, 0)    33.0(1, 3)    1.0(1, 4)    60.0(2, 0)    42.0(2, 1)    1.0(2, 4)    80.0
特征名字：['age' 'city=北京' 'city=成都' 'city=重庆' 'temperature']

(4)稀疏矩阵转为数组

稀疏矩阵对象调用toarray()函数, 得到类型为ndarray的二维稀疏矩阵

4 CountVectorizer 文本特征提取

(1)API

sklearn.feature_extraction.text.CountVectorizer

构造函数关键字参数stop_words，值为list，表示词的黑名单(不提取的词)

fit_transform函数的返回值为稀疏矩阵

(2) 英文文本提取

from sklearn.feature_extraction.text import CountVectorizer
import pandas as pd
data=["stu is well, stu is great", "You like stu"]
#创建转换器对象, you和is不提取
transfer = CountVectorizer(stop_words=["you","is"])
#进行提取,得到稀疏矩阵
data_new = transfer.fit_transform(data)
print(data_new)
​
import pandas
pandas.DataFrame(data_new.toarray(), index=["第一个句子","第二个句子"],columns=transfer.get_feature_names_out())

(3) 中文文本提取

a.中文文本不像英文文本，中文文本文字之间没有空格，所以要先分词，一般使用jieba分词.

b.下载jieba组件, (不要使用conda)

c.jieba的基础

import jieba
data = "在如今的互联网世界，正能量正成为澎湃时代的大流量"
data = jieba.cut(data)
data = list(data)
print(data) #['在', '如今', '的', '互联网', '世界', '，', '正', '能量', '正', '成为', '澎湃', '时代', '的', '大', '流量']
data = " ".join(data)
print(data) #"在 如今 的 互联网 世界 ， 正 能量 正 成为 澎湃 时代 的 大 流量"

使用jieba封装一个函数，功能是把汉语字符串中进行分词(会忽略长度小于等于1的词语,因为它们往往缺乏语义信息，不能很好地表达文本的特征)

import jieba
from sklearn.feature_extraction.text import CountVectorizer
data = ['陶吉吉唱了二十二', '周杰伦唱了园游会', '王力宏唱了爱错']
def fenci(str):return " ".join(list(jieba.cut(str)))
data = [fenci(str) for str in data]
print(data)
cv = CountVectorizer(stop_words=["唱了"])
data = cv.fit_transform(data)
print(data.toarray())
print(cv.get_feature_names_out())

5 TfidfVectorizer TF-IDF文本特征词的重要程度特征提取

(1) 算法

词频(Term Frequency, TF), 表示一个词在当前篇文章中的重要性

逆文档频率(Inverse Document Frequency, IDF), 反映了词在整个文档集合中的稀有程度

(2) API

sklearn.feature_extraction.text.TfidfVectorizer()

构造函数关键字参数stop_words，表示词特征黑名单

fit_transform函数的返回值为稀疏矩阵

(3) 示例

代码与CountVectorizer的示例基本相同,仅仅把CountVectorizer改为TfidfVectorizer即可

示例中data是一个字符串list, list中的第一个元素就代表一篇文章.

补充:在sklearn库中 TF-IDF算法做了一些细节的优化

词频 (TF)

词频是指一个词在文档中出现的频率。通常有两种计算方法：

1. 原始词频：一个词在文档中出现的次数除以文档中总的词数。

2. 平滑后的词频：为了防止高频词主导向量空间，有时会对词频进行平滑处理，例如使用 1 + log(TF)。

3. 在 TfidfVectorizer 中，TF 默认是：直接使用一个词在文档中出现的次数也就是CountVectorizer的结果

逆文档频率 (IDF)

逆文档频率衡量一个词的普遍重要性。如果一个词在许多文档中都出现，那么它的重要性就会降低。

IDF 的计算公式是：

IDF(t)=\log⁡(\dfrac{总文档数}{包含词t的文档数+1})

在 TfidfVectorizer 中，IDF 的默认计算公式是：

IDF(t)=\log⁡(\dfrac{总文档数+1}{包含词t的文档数+1})+1

在 TfidfVectorizer 中还会进行归一化处理(采用的L2归一化)

L2归一化

x_1归一化后的数据=\dfrac{x_1}{\sqrt{x_1^2+x_2^2+...x_n^2}}

x可以选择是行或者列的数据

from sklearn.feature_extraction.text import CountVectorizer,TfidfVectorizer
from sklearn.preprocessing import normalize
from sklearn.preprocessing import StandardScaler
import jieba
import pandas as pd
import numpy as np
def my_cut(text):return " ".join(jieba.cut(text))
data=["教育学会会长期间，坚定支持民办教育事业！",  "扶持民办,学校发展事业","事业做出重大贡献！"]
data=[my_cut(i) for i in data]
print(data)
# print("词频",CountVectorizer().fit_transform(data).toarray())
transfer=TfidfVectorizer()
res=transfer.fit_transform(data)
print(pd.DataFrame(res.toarray(),columns=transfer.get_feature_names_out()))
​
​
​
​
# 手动实现tfidf向量(跟上面的api实现出一样的效果)
def tfidf(data):# 计算词频count = CountVectorizer().fit_transform(data).toarray()print("count",count)print(np.sum(count != 0, axis=0))# 计算IDF，并采用平滑处理idf = np.log((len(data) + 1) / (1 + np.sum(count != 0, axis=0))) + 1# 计算TF-IDFtf_idf = count * idf# L2标准化tf_idf_normalized = normalize(tf_idf, norm='l2', axis=1)#axis=0是列  axis=1是行return tf_idf,tf_idf_normalized
tf_idf,tf_idf_normalized=tfidf(data)
print(pd.DataFrame(tf_idf,columns=transfer.get_feature_names_out()))
print(pd.DataFrame(tf_idf_normalized,columns=transfer.get_feature_names_out()))

6 无量纲化-预处理

无量纲，即没有单位的数据

无量纲化包括"归一化"和"标准化", 为什么要进行无量纲化呢?

这是一个男士的数据表:

编号id	身高 h	收入 s	体重 w
1	1.75(米)	15000(元)	120(斤)
2	1.5(米)	16000(元)	140(斤)
3	1.6(米)	20000(元)	100(斤)

假设算法中需要求它们之间的欧式距离, 这里以编号1和编号2为示例:

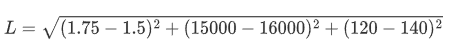
从计算上来看, 发现身高对计算结果没有什么影响, 基本主要由收入来决定了,但是现实生活中,身高是比较重要的判断标准. 所以需要无量纲化.

(1) MinMaxScaler 归一化

通过对原始数据进行变换把数据映射到指定区间(默认为0-1)

<1>归一化公式:

这里的 𝑥min 和 𝑥max 分别是每种特征中的最小值和最大值，而 𝑥是当前特征值，𝑥scaled 是归一化后的特征值。

若要缩放到其他区间，可以使用公式：x=x*(max-min)+min;

比如 [-1, 1]的公式为:

<2>归一化API

sklearn.preprocessing.MinMaxScaler(feature_range)

参数:feature_range=(0,1) 归一化后的值域,可以自己设定

fit_transform函数归一化的原始数据类型可以是list、DataFrame和ndarray, 不可以是稀疏矩阵

fit_transform函数的返回值为ndarray

<3>归一化示例

示例1：原始数据类型为list

from sklearn.preprocessing import MinMaxScaler
tool  = MinMaxScaler(feature_range=(0,1))
x = [[100,2],[800,3],[300,7],[230,4]]
x =tool.fit_transform(x)
print(x)

示例2：原始数据类型为DataFrame

from sklearn.preprocessing import MinMaxScaler
import pandas as pd;
data=[[12,22,4],[22,23,1],[11,23,9]]
data = pd.DataFrame(data=data, index=["一","二","三"], columns=["一列","二列","三列"])
transfer = MinMaxScaler(feature_range=(0, 1))
data_new = transfer.fit_transform(data)
print(data_new)

示例3：原始数据类型为 ndarray

from sklearn.feature_extraction import DictVectorizer
from sklearn.preprocessing import MinMaxScaler
​
data = [{'city':'成都', 'age':30, 'temperature':200}, {'city':'重庆','age':33, 'temperature':60}, {'city':'北京', 'age':42, 'temperature':80}]
transfer = DictVectorizer(sparse=False)
data = transfer.fit_transform(data) #data类型为ndarray
print(data)
​
transfer = MinMaxScaler(feature_range=(0, 1))
data = transfer.fit_transform(data)
print(data)

<4>缺点

最大值和最小值容易受到异常点影响，所以鲁棒性较差。所以常使用标准化的无量钢化

(2)normalize归一化

API

from sklearn.preprocessing import normalize
normalize(data, norm='l2', axis=1)
#data是要归一化的数据
#norm是使用那种归一化:"l1"  "l2"  "max
#axis=0是列  axis=1是行

<1> L1归一化

绝对值相加作为分母,特征值作为分子

<2> L2归一化

平方相加作为分母,特征值作为分子

<3> max归一化

max作为分母,特征值作为分子

from sklearn.preprocessing import normalize
x = [[100,2],[800,3],[300,7],[230,4]]
x = normalize(x,norm='max',axis=0)
print(x)

(3)StandardScaler 标准化

在机器学习中，标准化是一种数据预处理技术，也称为数据归一化或特征缩放。它的目的是将不同特征的数值范围缩放到统一的标准范围，以便更好地适应一些机器学习算法，特别是那些对输入数据的尺度敏感的算法。

<1>标准化公式

最常见的标准化方法是Z-score标准化，也称为零均值标准化。它通过对每个特征的值减去其均值，再除以其标准差，将数据转换为均值为0，标准差为1的分布。这可以通过以下公式计算:

其中，z是转换后的数值，x是原始数据的值，μ是该特征的均值，σ是该特征的 标准差

<2> 标准化 API

sklearn.preprocessing.StandardScale

与MinMaxScaler一样，原始数据类型可以是list、DataFrame和ndarray

fit_transform函数的返回值为ndarray, 归一化后得到的数据类型都是ndarray

from sklearn.preprocessing import StandardScaler
#不能加参数feature_range=(0, 1)
transfer = StandardScaler()
data_new = transfer.fit_transform(data) #data_new的类型为ndarray

<3>标准化示例

from sklearn.preprocessing import StandardScaler
x = [[100,2],[800,3],[300,7],[230,4]]
tool = StandardScaler()
x = tool.fit_transform(x)
print(x)

<4> 注意点

在数据预处理中，特别是使用如StandardScaler这样的数据转换器时，fit、fit_transform和transform这三个方法的使用是至关重要的，它们各自有不同的作用：

1. fit:

   • 这个方法用来计算数据的统计信息，比如均值和标准差（在StandardScaler的情况下）。这些统计信息随后会被用于数据的标准化。

   • 你应当仅在训练集上使用fit方法。

2. fit_transform:

   • 这个方法相当于先调用fit再调用transform，但是它在内部执行得更高效。

   • 它同样应当仅在训练集上使用，它会计算训练集的统计信息并立即应用到该训练集上。

3. transform:

   • 这个方法使用已经通过fit方法计算出的统计信息来转换数据。

   • 它可以应用于任何数据集，包括训练集、验证集或测试集，但是应用时使用的统计信息必须来自于训练集。

当你在预处理数据时，首先需要在训练集X_train上使用fit_transform，这样做可以一次性完成统计信息的计算和数据的标准化。这是因为我们需要确保模型是基于训练数据的统计信息进行学习的，而不是整个数据集的统计信息。

一旦scaler对象在X_train上被fit，它就已经知道了如何将数据标准化。这时，对于测试集X_test，我们只需要使用transform方法，因为我们不希望在测试集上重新计算任何统计信息，也不希望测试集的信息影响到训练过程。如果我们对X_test也使用fit_transform，测试集的信息就可能会影响到训练过程。

总结来说:我们常常是先fit_transform(x_train)然后再transform(x_text)

7 特征降维

实际数据中,有时候特征很多,会增加计算量,降维就是去掉一些特征,或者转化多个特征为少量个特征

特征降维其目的:是减少数据集的维度，同时尽可能保留数据的重要信息。

特征降维的好处:

减少计算成本：在高维空间中处理数据可能非常耗时且计算密集。降维可以简化模型，降低训练时间和资源需求。

去除噪声：高维数据可能包含许多无关或冗余特征，这些特征可能引入噪声并导致过拟合。降维可以帮助去除这些不必要的特征。

特征降维的方式:

• 特征选择

  • 从原始特征集中挑选出最相关的特征

• 主成份分析(PCA)

  • 主成分分析就是把之前的特征通过一系列数学计算，形成新的特征，新的特征数量会小于之前特征数量

1 .特征选择

(a) VarianceThreshold 低方差过滤特征选择

• Filter(过滤式): 主要探究特征本身特点， 特征与特征、特征与目标 值之间关联

  • 方差选择法: 低方差特征过滤

    如果一个特征的方差很小，说明这个特征的值在样本中几乎相同或变化不大，包含的信息量很少，模型很难通过该特征区分不同的对象,比如区分甜瓜子和咸瓜子还是蒜香瓜子,如果有一个特征是长度,这个特征相差不大可以去掉。

    1. 计算方差：对于每个特征，计算其在训练集中的方差(每个样本值与均值之差的平方,在求平均)。

    2. 设定阈值：选择一个方差阈值，任何低于这个阈值的特征都将被视为低方差特征。

    3. 过滤特征：移除所有方差低于设定阈值的特征

# 特征降维
from sklearn.feature_selection import VarianceThreshold
tool = VarianceThreshold(threshold=1.5)
x = [[10, 2],[11,6],[10,8],[10,10],[10,19]]
x = tool.fit_transform(x)
print(x)

(b) 根据相关系数的特征选择

<1>理论

正相关性（Positive Correlation）是指两个变量之间的一种统计关系，其中一个变量的增加通常伴随着另一个变量的增加，反之亦然。在正相关的关系中，两个变量的变化趋势是同向的。当我们说两个变量正相关时，意味着：

• 如果第一个变量增加，第二个变量也有很大的概率会增加。

• 同样，如果第一个变量减少，第二个变量也很可能会减少。

正相关性并不意味着一个变量的变化直接引起了另一个变量的变化，它仅仅指出了两个变量之间存在的一种统计上的关联性。这种关联性可以是因果关系，也可以是由第三个未观察到的变量引起的，或者是纯属巧合。

在数学上，正相关性通常用正值的相关系数来表示，这个值介于0和1之间。当相关系数等于1时，表示两个变量之间存在完美的正相关关系，即一个变量的值可以完全由另一个变量的值预测。

举个例子，假设我们观察到在一定范围内，一个人的身高与其体重呈正相关，这意味着在一般情况下，身高较高的人体重也会较重。但这并不意味着身高直接导致体重增加，而是可能由于营养、遗传、生活方式等因素共同作用的结果。

负相关性（Negative Correlation）与正相关性刚好相反,但是也说明相关,比如运动频率和BMI体重指数程负相关

不相关指两者的相关性很小,一个变量变化不会引起另外的变量变化,只是没有线性关系. 比如饭量和智商

皮尔逊相关系数（Pearson correlation coefficient)是一种度量两个变量之间线性相关性的统计量。它提供了两个变量间关系的方向（正相关或负相关）和强度的信息。皮尔逊相关系数的取值范围是 [−1,1]，其中：

• \rho=1 表示完全正相关，即随着一个变量的增加，另一个变量也线性增加。

• \rho=-1 表示完全负相关，即随着一个变量的增加，另一个变量线性减少。

• \rho=0 表示两个变量之间不存在线性关系。

相关系数\rho的绝对值为0-1之间，绝对值越大，表示越相关，当两特征完全相关时，两特征的值表示的向量是

在同一条直线上，当两特征的相关系数绝对值很小时，两特征值表示的向量接近在同一条直线上。当相关系值为负数时，表示负相关

<2>皮尔逊相关系数:pearsonr相关系数计算公式, 该公式出自于概率论

对于两组数据 𝑋={𝑥1,𝑥2,...,𝑥𝑛} 和 𝑌={𝑦1,𝑦2,...,𝑦𝑛}，皮尔逊相关系数可以用以下公式计算：

\bar{x}和 \bar{y} 分别是𝑋和𝑌的平均值

|ρ|<0.4为低度相关; 0.4<=|ρ|<0.7为显著相关； 0.7<=|ρ|<1为高度相关

<3>api:

scipy.stats.personr(x, y) 计算两特征之间的相关性

返回对象有两个属性:

statistic皮尔逊相关系数[-1,1]

pvalue零假设(了解),统计上评估两个变量之间的相关性,越小越相关

<4>示例：

# 皮尔逊相关系数
from scipy.stats import pearsonr
x = [10,20,30,40,50]
x2 =[10,20,1,40,77]
y = [1,2,3,4,5]
res = pearsonr(x2,y)
print(res.statistic) # 相关系数
print(res.pvalue) # p值 越小越好

开发中一般不使用求相关系数的方法，一般使用主成分分析，因为主成分分样过程中就包括了求相关系数了。

2.主成份分析(PCA)

PCA的核心目标是从原始特征空间中找到一个新的坐标系统，使得数据在新坐标轴上的投影能够最大程度地保留数据的方差，同时减少数据的维度。

(a) 原理

x_0投影到L的大小为x_0*cos \alpha

y_0投影到L的大小为y_0*sin\alpha

使用(x_0,y_0)表示一个点， 表明该点有两个特征， 而映射到L上有一个特征就可以表示这个点了。这就达到了降维的功能 。

投影到L上的值就是降维后保留的信息，投影到与L垂直的轴上的值就是丢失的信息。保留信息/原始信息=信息保留的比例

下图中红线上点与点的距离是最大的，所以在红色线上点的方差最大，粉红线上的刚好相反.

所以红色线上点来表示之前点的信息损失是最小的。

(b) 步骤

• 得到矩阵

• 用矩阵P对原始数据进行线性变换，得到新的数据矩阵Z,每一列就是一个主成分, 如下图就是把10维降成了2维,得到了两个主成分

  

• 根据主成分的方差等，确定最终保留的主成分个数， 方差大的要留下。一个特征的多个样本的值如果都相同，则方差为0， 则说明该特征值不能区别样本，所以该特征没有用。

比如下图的二维数据要降为一维数据，图形法是把所在数据在二维坐标中以点的形式标出，然后给出一条直线，让所有点垂直映射到直线上，该直线有很多，只有点到线的距离之和最小的线才能让之前信息损失最小。

这样之前所有的二维表示的点就全部变成一条直线上的点，从二维降成了一维。

上图是一个从二维降到一维的示例：的原始数据为

特征1-X1	特征2-X2
-1	-2
-1	0
0	0
2	1
0	1

降维后新的数据为

特征3-X0
-3/√2
-1/√2
0
3/√2
-1/√2

3.api

• from sklearn.decomposition import PCA

• PCA(n_components=None)

  • 主成分分析

  • n_components:

    • 实参为小数时：表示降维后保留百分之多少的信息

    • 实参为整数时：表示减少到多少特征

from sklearn.decomposition import PCA
data = [[2,18,4,5],[6,32,10,8],[5,43,93,1]]
# 信息保留50% 但是不确定会保留几个
pca = PCA(n_components=0.5)
data = pca.fit_transform(data)
print(data)

#鸢尾花 特征降维
from sklearn.datasets import load_iris
from sklearn.decomposition import PCA
x,y = load_iris(return_X_y=True)
pca = PCA(n_components=2)
# pca.fit(x)
# x_pca = pca.transform(x)
x = pca.fit_transform(x)
print(x.shape)
print(x)