数据结构-二叉树经典OJ题
文章目录
- 一、单值二叉树
- 二、相同的树
- 三、对称二叉树
- 四、另一棵树的子树
- 五、二叉树遍历
- 5.1前序遍历
- 5.2 二叉树的构建及遍历
一、单值二叉树
(链接：UnivaluedBinaryTree)
bool isUnivalTree(struct TreeNode* root)
{
if(root == NULL)
return true;
if(root->left != NULL && root->left->val != root->val)
return false;
if(root->right != NULL && root->right->val != root->val)
return false;
return isUnivalTree(root->left)
&& isUnivalTree(root->right);
}
如果一棵树是单值二叉树的话，则父子节点之间的值一定是相等的：
a == b && b == c 则推出 a == b == c
所以通过传递比较的性质就可以判断出一棵二叉树是否是单值二叉树。
二、相同的树
(链接：SameTree)
bool isSameTree(struct TreeNode* p, struct TreeNode* q)
{
if(p==NULL && q==NULL)
return true;
if(p==NULL || q==NULL)
return false;
if(p->val != q->val)
return false;
return isSameTree(p->left,q->left)
&& isSameTree(p->right,q->right);
}
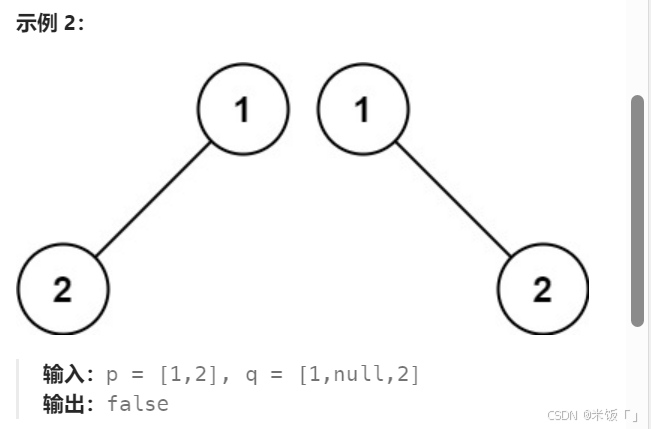
两棵二叉树相同就是根相同，左右子树也相同。
三、对称二叉树
(链接：SymmetricTree)
由于题目给定的树的是至少有一个节点的，所以根节点就不用判断是否对称啦，直接从根节点的左右子树开始判断是否对称：
bool _isSymmetric(struct TreeNode* leftRoot,struct TreeNode* rightRoot)
{
if(leftRoot == NULL && rightRoot == NULL)
return true;
if(leftRoot == NULL || rightRoot == NULL)
return false;
if(leftRoot->val != rightRoot->val)
return false;
return _isSymmetric(leftRoot->left,rightRoot->right)
&& _isSymmetric(leftRoot->right,rightRoot->left);
}
bool isSymmetric(struct TreeNode* root)
{
return _isSymmetric(root->left,root->right);
}
四、另一棵树的子树
(链接：SubtreeOfAnotherTree)
这道题需要借助前面做过的题：判断是否是相同的树那题来做此题。对于二叉树的每个不为空的节点都可以看作是其所在子树的根。所以我们可以通过前序遍历的方法判断root中是否包含subRoot这棵子树：
bool isSameTree(struct TreeNode* p, struct TreeNode* q)
{
if(p == NULL && q == NULL)
return true;
if(p == NULL || q == NULL)
return false;
if(p->val != q->val)
return false;
return isSameTree(p->left,q->left)
&& isSameTree(p->right,q->right);
}
bool isSubtree(struct TreeNode* root, struct TreeNode* subRoot)
{
if(root == NULL)
return false;
if(isSameTree(root,subRoot))
return true;
return isSubtree(root->left,subRoot)
|| isSubtree(root->right,subRoot);
}
五、二叉树遍历
5.1前序遍历
(链接：BTreePrevOrder)
//计算二叉树节点数量
int TreeSize(struct TreeNode* root)
{
if(root==NULL)
return 0;
return TreeSize(root->left)+TreeSize(root->right)+1;
}
//前序遍历二叉树,并将值存放进数组a中
void _preorder(struct TreeNode* root, int*a, int* pi)
{
if(root == NULL)
return;
a[(*pi)++] = root->val;
_preorder(root->left, a, pi);
_preorder(root->right, a, pi);
}
//前序遍历的主调函数
int* preorderTraversal(struct TreeNode* root, int* returnSize)
{
*returnSize = TreeSize(root);
int* arr = (int*)malloc((*returnSize)*sizeof(int));
if(arr == NULL)
{
exit(1);
}
int i = 0;//数组arr的下标
_preorder(root,arr,&i);
return arr;
}
这里需要注意的是preorderTraversal函数的参数中有一个returnSize参数，这个参数不是直接拿来使用的，它是用来接收计算出的二叉树的节点个数的，也叫输出型参数。为什么returnSize是一个指针呢？因为需要知道数组中的有效元素个数，所以传指针是为了让returnSize一直记录着二叉树的节点个数，方便编译器获取returnSize。试想：如果returnSize是值传递的话，则preorderTraversal函数调用完毕后，函数外边的returnSize就没有记录下数组的有效数据个数。
5.2 二叉树的构建及遍历
(链接：Practice)
这道题是要先通过先序序列构建出二叉树，然后再对二叉树进行中序遍历：
#include <stdio.h>
#include<stdlib.h>
typedef char BTDataType;
typedef struct BinaryTreeNode
{
struct BinaryTreeNode* left; // 指向当前结点的左孩子
struct BinaryTreeNode* right; // 指向当前结点的右孩子
BTDataType val; // 当前结点的值域
} BTNode;
BTNode* BuyBTNode(char x)
{
BTNode* newnode = (BTNode*)malloc(sizeof(BTNode));
if (newnode == NULL)
{
perror("malloc fail");
return NULL;
}
newnode->val = x;
newnode->left = NULL;
newnode->right = NULL;
return newnode;
}
//创建二叉树
BTNode* CreateTree(char* a,int* pi)
{
if(a[*pi] == '#')
{
(*pi)++;
return NULL;
}
BTNode* root = BuyBTNode(a[*pi]);
(*pi)++;
root->left = CreateTree(a,pi);
root->right = CreateTree(a,pi);
return root;
}
//中序遍历
void InOrder(BTNode* root)
{
if(root == NULL)
{
return;
}
InOrder(root->left);
printf("%c ",root->val);
InOrder(root->right);
}
int main()
{
char arr[100];
scanf("%s",arr);
int i = 0;
BTNode* root = CreateTree(arr,&i);
InOrder(root);
return 0;
}
注意i是一个全局变量，这样调用CreateTree函数时传i的地址，就能改变全局变量i。
补充：
在C语言中，函数参数可以分为两种类型：输入型参数（也称为输入参数或传入参数）和输出型参数（也称为传出参数或输出参数）。这两种参数在函数中的作用和用法略有不同。
1.输入型参数（Input Parameters）
输入型参数是在调用函数时从函数外部传递给函数的值。这些值在函数内部被读取，但在函数执行过程中不会被修改。输入型参数主要用于向函数提供必要的信息或数据，以便函数可以基于这些数据进行计算或处理。
2.输出型参数（Output Parameters）
输出型参数用于从函数返回数据到函数外部。这通常通过引用（在C语言中通过指针实现）来实现，即通过传递变量的地址给函数，函数内部可以修改这个变量的值，从而影响函数外部的变量。
🔥总结：
🍃输入型参数：在函数调用时传递给函数的值，不应在函数内部被修改。
🍃输出型参数：通过指针传递变量的地址，函数内部可以修改这个变量的值，从而影响函数外部的变量。这在需要从函数返回多个值或者需要修改外部变量时非常有用。
理解这两种参数的差异和用法对于编写高效、清晰的C语言代码至关重要。