5.4学习记录
今天的目标是复习+刷过往的提高课的DP题目:重点是数位DP,状态压缩DP,然后去做一些新的DP题目
然后明天的任务就是把DP的题目汇总,复习一些疑难的问题
方格取数:
题目背景
NOIP 2000 提高组 T4
题目描述
设有 N×N 的方格图 (N≤9),我们将其中的某些方格中填入正整数,而其他的方格中则放入数字 0。如下图所示(见样例):

某人从图的左上角的 A 点出发,可以向下行走,也可以向右走,直到到达右下角的 B 点。在走过的路上,他可以取走方格中的数(取走后的方格中将变为数字 0)。
此人从 A 点到 B 点共走两次,试找出 2 条这样的路径,使得取得的数之和为最大。
输入格式
输入的第一行为一个整数 N(表示 N×N 的方格图),接下来的每行有三个整数,前两个表示位置,第三个数为该位置上所放的数。一行单独的 0 表示输入结束。
输出格式
只需输出一个整数,表示 2 条路径上取得的最大的和。
一次的走法:
f[i1][j1][i2][j2] 表示两个路径,从(1,1)走到(i1,j1),从(1,1)走到(i2,j2)
什么时候两个路径会重合尼?:
显然当他们重合的时候有i1+j1==i2+j2这个是很显然的
所以我们可以用k表示总步数
f[k][i1][i2]表示我们需要考虑的情况(其他状态下一步他们两个一定不会重合)
j1=k-i1 j2=k-i2
下面看我们的状态转移的方程:
四个推广的方向:
1下2下,1下2右,1右2右,1右2下
当然要判断一下这两个点走完过后不能够到同一个位置
如果重合的话,只加一次w(i,j)
如果没有重合的话,就要加上两次
代码:
#include<bits/stdc++.h>
using namespace std;
const int N=15;
int w[N][N];
int f[N*2][N][N];
int n;
int main(){
cin>>n;
while(1){
int x,y,c;
cin>>x>>y>>c;
if(x==0&&y==0&&c==0)break;
w[x][y]=c;
}
for(int k=2;k<=2*n;k++){
for(int i=1;i<=n;i++){
for(int j=1;j<=n;j++){
int ii=k-i;
int jj=k-j;
if(ii<1||jj<1)continue;
if(ii>n||jj>n)continue;
int val=w[i][ii];
if(i!=j)val+=w[j][jj];
f[k][i][j]=max(f[k][i][j],f[k-1][i-1][j-1]+val);
f[k][i][j]=max(f[k][i][j],f[k-1][i][j-1]+val);
f[k][i][j]=max(f[k][i][j],f[k-1][i][j]+val);
f[k][i][j]=max(f[k][i][j],f[k-1][i-1][j]+val);
}
}
}
cout<<f[2*n][n][n];
}
导弹防御系统:
为了对抗附近恶意国家的威胁,RR 国更新了他们的导弹防御系统。
一套防御系统的导弹拦截高度要么一直 严格单调 上升要么一直 严格单调 下降。
例如,一套系统先后拦截了高度为 33 和高度为 44 的两发导弹,那么接下来该系统就只能拦截高度大于 44 的导弹。
给定即将袭来的一系列导弹的高度,请你求出至少需要多少套防御系统,就可以将它们全部击落。
输入格式
输入包含多组测试用例。
对于每个测试用例,第一行包含整数 nn,表示来袭导弹数量。
第二行包含 nn 个不同的整数,表示每个导弹的高度。
当输入测试用例 n=0n=0 时,表示输入终止,且该用例无需处理。
输出格式
对于每个测试用例,输出一个占据一行的整数,表示所需的防御系统数量。
代码:
#include<bits/stdc++.h>
using namespace std;
const int N=55;
int a[N];
int n;
int up[N];
int down[N];
int ans=0x3f3f3f3f;
void dfs(int pos,int pu,int pd){
if(pu+pd>=ans)return;
if(pos==n+1){
ans=min(ans,pu+pd);
return;
}
//放入上升序列
int k=0;
while(k<pu&&a[pos]<=up[k])k++;
int back=up[k];
up[k]=a[pos];
if(k>=pu){
dfs(pos+1,pu+1,pd);
}else dfs(pos+1,pu,pd);
up[k]=back;
//放入下降序列
k=0;
while(k<pd&&a[pos]>=down[k])k++;
back=down[k];
down[k]=a[pos];
if(k>=pd){
dfs(pos+1,pu,pd+1);
}else dfs(pos+1,pu,pd);
down[k]=back;
}
int main(){
while(scanf("%d",&n),n!=0){
for(int i=1;i<=n;i++)scanf("%d",&a[i]);
ans=0x3f3f3f3f;
memset(up,0,sizeof up);
memset(down,0,sizeof up);
dfs(1,0,0);
cout<<ans<<endl;
}
}
最长公共子序列:
(融合了LIS的nlogn的LCS)
题目描述
给出 1,2,…,n 的两个排列 P1 和 P2 ,求它们的最长公共子序列。
输入格式
第一行是一个数 n。
接下来两行,每行为 n 个数,为自然数 1,2,…,n 的一个排列。
输出格式
一个数,即最长公共子序列的长度。
#include<iostream>
#include<cstdio>
using namespace std;
int a[100001],b[100001],map[100001],f[100001];
int main()
{
int n;
cin>>n;
for(int i=1;i<=n;i++){scanf("%d",&a[i]);map[a[i]]=i;}
for(int i=1;i<=n;i++){scanf("%d",&b[i]);f[i]=0x7fffffff;}
int len=0;
f[0]=0;
for(int i=1;i<=n;i++)
{
int l=0,r=len,mid;
int ans=0;
if(map[b[i]]>f[len])f[++len]=map[b[i]];//f存的是长度为i的最后一个数的位置,如果和b[i]相等的a[i],可以接在最长的len后面
else //不能接在最后面,就找到所有已有长度中最长的,满足f[ans]<map[b[i]],以此去更新f[ans+1]
{
while(l<=r)
{
mid=(l+r)/2;
if(f[mid]>map[b[i]]){//不能接在后面
r=mid-1;
}
else if(f[mid]<map[b[i]]){//可以接在f[mid]后面,去找找更长的
ans=mid;
l=mid+1;
}
}
f[ans+1]=min(map[b[i]],f[ans+1]);//可以接在ans后面,尝试去更新ans+1长度的最后一个值的更小的位置
}
}
cout<<len;
return 0;
}
最长上升子序列:
题目描述
这是一个简单的动规板子题。
给出一个由 n(n≤5000) 个不超过 106 的正整数组成的序列。请输出这个序列的最长上升子序列的长度。
最长上升子序列是指,从原序列中按顺序取出一些数字排在一起,这些数字是逐渐增大的。
输入格式
第一行,一个整数 n,表示序列长度。
第二行有 n 个整数,表示这个序列。
#include <bits/stdc++.h>
using namespace std;
const int N=5010;
int n;
int a[N];
int f[N];
int main(){
cin>>n;
for(int i=1;i<=n;i++){
scanf("%d",&a[i]);
}
int len=0;
memset(f,0x3f,sizeof f);
f[0]=0;
for(int i=1;i<=n;i++){
int l=0,r=len;
int ans=0;
if(f[len]<a[i])f[++len]=a[i];//可以接在最后面
else{//尝试优化内部结构
while(l<=r){
int mid=(l+r)/2;
if(f[mid]>=a[i]){
r=mid-1;
}else if(f[mid]<a[i]){
ans=mid;
l=mid+1;
}
}
//可以接在ans的后面
f[ans+1]=min(f[ans+1],a[i]);
}
}
cout<<len;
}
货币系统:
题目背景
NOIP2018 提高组 D1T2
题目描述
在网友的国度中共有 n 种不同面额的货币,第 i 种货币的面额为 a[i],你可以假设每一种货币都有无穷多张。为了方便,我们把货币种数为 n、面额数组为 a[1..n] 的货币系统记作 (n,a)。
在一个完善的货币系统中,每一个非负整数的金额 x 都应该可以被表示出,即对每一个非负整数 x,都存在 n 个非负整数 t[i] 满足 a[i]×t[i] 的和为 x。然而, 在网友的国度中,货币系统可能是不完善的,即可能存在金额 x 不能被该货币系统表示出。例如在货币系统 n=3, a=[2,5,9] 中,金额 1,3 就无法被表示出来。
两个货币系统 (n,a) 和 (m,b) 是等价的,当且仅当对于任意非负整数 x,它要么均可以被两个货币系统表出,要么不能被其中任何一个表出。
现在网友们打算简化一下货币系统。他们希望找到一个货币系统 (m,b),满足 (m,b) 与原来的货币系统 (n,a) 等价,且 m 尽可能的小。他们希望你来协助完成这个艰巨的任务:找到最小的 m。
输入格式
输入文件的第一行包含一个整数 T,表示数据的组数。
接下来按照如下格式分别给出 T 组数据。 每组数据的第一行包含一个正整数 n。接下来一行包含 n 个由空格隔开的正整数 a[i]。
输出格式
输出文件共有 T 行,对于每组数据,输出一行一个正整数,表示所有与 (n,a) 等价的货币系统 (m,b) 中,最小的 m。
代码:
#include <bits/stdc++.h>
using namespace std;
const int N=150;
int a[N];
int f[300000];
int n;
int t;
bool st[N];
int main(){
scanf("%d",&t);
while(t--){
scanf("%d",&n);
for(int i=1;i<=n;i++)scanf("%d",&a[i]);
sort(a+1,a+1+n);
memset(f,0,sizeof f);
f[0]=1;
int res=0;
for(int i=1;i<=n;i++){
if(f[a[i]])continue;
res++;
for(int j=a[i];j<=a[n];j++){
f[j]=f[j]|f[j-a[i]];
}
}
cout<<res<<endl;
}
}
有依赖的背包问题
有 N个物品和一个容量是 V 的背包。
物品之间具有依赖关系,且依赖关系组成一棵树的形状。如果选择一个物品,则必须选择它的父节点。
如下图所示:
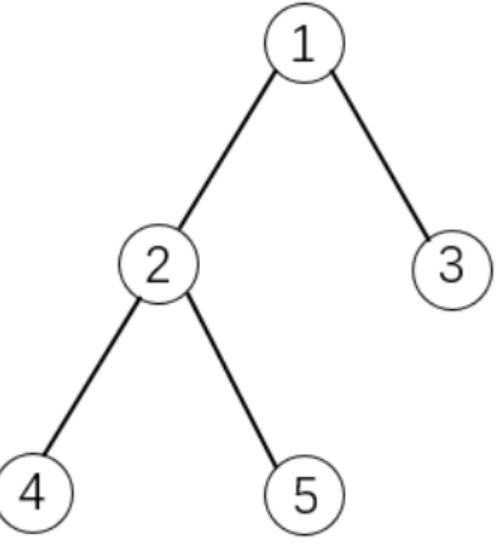
如果选择物品5,则必须选择物品1和2。这是因为2是5的父节点,1是2的父节点。
每件物品的编号是 ii,体积是 vivi,价值是 wiwi,依赖的父节点编号是 pipi。物品的下标范围是 1…N1…N。
求解将哪些物品装入背包,可使物品总体积不超过背包容量,且总价值最大。
输出最大价值。
输入格式
第一行有两个整数 N,VN,V,用空格隔开,分别表示物品个数和背包容量。
接下来有 NN 行数据,每行数据表示一个物品。
第 ii 行有三个整数 vi,wi,pivi,wi,pi,用空格隔开,分别表示物品的体积、价值和依赖的物品编号。
如果 pi=−1pi=−1,表示根节点。 数据保证所有物品构成一棵树。
输出格式
输出一个整数,表示最大价值。
数据范围
1≤N,V≤1001≤N,V≤100
1≤vi,wi≤1001≤vi,wi≤100
父节点编号范围:
内部结点:1≤pi≤N1≤pi≤N;
根节点 pi=−1pi=−1
代码:
#include<bits/stdc++.h>
using namespace std;
const int N=110;
int f[N][N];
int v[N],w[N];
unordered_map<int,vector<int>>e;
int n,m;
void dfs(int u){
for(int to:e[u]){
dfs(to);
for(int j=m;j>=w[u];j--){//循环 子树 使用体积,最少是w[u]
for(int k=w[u];k<=j;k++)//循环 根 用的体积,最少是w[u]
f[u][j]=max(f[u][j],f[u][k]+f[to][j-k]);//f[u][k]+f[to][j-k]
}
}
for(int j=w[u];j<=m;j++)f[u][j]+=v[u];
}
int main(){
scanf("%d%d",&n,&m);
int root=0;
for(int i=1;i<=n;i++){
int a,b,c;
scanf("%d%d%d",&b,&a,&c);
v[i]=a;
w[i]=b;
if(c==-1)root=i;
else e[c].push_back(i);
}
dfs(root);
cout<<f[root][m];
}
状态压缩dp基础:
二进制枚举
#include<bits/stdc++.h>
using namespace std;
int n;
void op(int x){
for(int i=0;i<n;i++){
if((x>>i)&1){
cout<<i+1<<' ';
}
}
}
int main(){
scanf("%d",&n);
for(int i=0;i<1<<n;i++){
op(i);
if(i+1!=1<<n)cout<<endl;
}
}
棋盘型状态压缩dp
蒙德里安的梦想:
求把 N×MN×M 的棋盘分割成若干个 1×21×2 的长方形,有多少种方案。
例如当 N=2,M=4N=2,M=4 时,共有 55 种方案。当 N=2,M=3N=2,M=3 时,共有 33 种方案。
如下图所示:

输入格式
输入包含多组测试用例。
每组测试用例占一行,包含两个整数 NN 和 MM。
当输入用例 N=0,M=0N=0,M=0 时,表示输入终止,且该用例无需处理。
输出格式
每个测试用例输出一个结果,每个结果占一行。
#include <bits/stdc++.h>
using namespace std;
// 定义常量 N 表示棋盘的列数相关的一个上限值,M 表示所有可能的状态数(2 的 N 次方)
const int N = 12, M = 1 << N;
// f 数组用于动态规划,第一维表示列数,第二维表示每一列的所有可能状态,存储方案数
long long f[N][M];
// st 数组用于存储每种状态是否有奇数个连续的 0,若有奇数个连续 0 则该状态无效,否则为 true
bool st[M];
// state 是一个二维数组(这里用 vector<vector<int>> 实现),用于记录每一种状态下合法的前一列状态
vector<vector<int>> state(M);
int m, n; // m 表示棋盘的列数,n 表示棋盘的行数
int main() {
// 持续读入 n 和 m,只要 n 和 m 不同时为 0,就继续执行循环体
while (cin >> n >> m, n || m) {
// 遍历所有可能的状态(用二进制数表示,范围是 0 到 2 的 n 次方减 1)
for (int i = 0; i < (1 << n); i++) {
int cnt = 0; // 用于记录连续的 0 的个数
bool isValid = true; // 标记某种状态是否没有奇数个连续的 0,初始设为 true
// 遍历当前状态的每一位(对应棋盘的每一行),判断是否存在奇数个连续的 0
for (int j = 0; j < n; j++) {
// 判断状态 i 的二进制表示中第 j 位是否为 1
if ((i >> j) & 1) {
// 如果当前位为 1,检查前面连续的 0 的个数是否为奇数
if (cnt & 1) {
// 如果是奇数个连续的 0,则该状态不合法,标记为 false 并跳出循环
isValid = false;
break;
}
// 重置连续 0 的计数器,因为当前位为 1,新的连续 0 计数开始
cnt = 0;
}
else {
// 当前位为 0,连续 0 的计数器加 1
cnt++;
}
}
// 检查最后一段连续的 0 的个数是否为奇数,如果是则状态不合法
if (cnt & 1)
isValid = false;
// 将状态 i 是否有奇数个连续 0 的情况记录到 st 数组中
st[i] = isValid;
}
// 遍历第 i 列的所有状态(用二进制数表示,范围是 0 到 2 的 n 次方减 1)
for (int j = 0; j < (1 << n); j++) {
// 清空上一次操作遗留的状态,避免影响本次状态的判断
state[j].clear();
// 遍历第 i - 1 列的所有状态(用二进制数表示,范围是 0 到 2 的 n 次方减 1)
for (int k = 0; k < (1 << n); k++) {
// 判断第 i 列的状态 j 和第 i - 1 列的状态 k 是否没有冲突(按位与为 0)
// 并且它们合并后的状态是合法的(st[j | k] 为 true)
if ((j & k) == 0 && st[j | k])
// 如果满足条件,则将第 i - 1 列的状态 k 记录为第 i 列状态 j 的合法前一状态
state[j].push_back(k);
}
}
// 动态规划部分开始,初始化 f 数组为 0
memset(f, 0, sizeof f);
// 初始化第 0 列,状态为 0 的方案数为 1
f[0][0] = 1;
// 遍历每一列(从第 1 列到第 m 列)
for (int i = 1; i <= m; i++) {
// 遍历当前列(第 i 列)的所有状态 j(用二进制数表示,范围是 0 到 2 的 n 次方减 1)
for (int j = 0; j < (1 << n); j++) {
// 遍历第 i - 1 列中与当前状态 j 合法的所有状态 k
for (auto k : state[j])
// 当前列状态 j 的方案数等于上一列(第 i - 1 列)状态 k 的方案数之和
f[i][j] += f[i - 1][k];
}
}
// 输出第 m 列,状态为 0 的方案数
cout << f[m][0] << endl;
}
return 0;
}
最短hamilton路径:
题目描述
给定一张 n 个点的带权无向图,点从 0∼n−1 标号,求起点 0 到终点 n−1 的最短 Hamilton 路径。
Hamilton 路径的定义是从 0 到 n−1 不重不漏地经过每个点恰好一次。
输入格式
第一行输入整数 n。
接下来 n 行每行 n 个整数,其中第 i 行第 j 个整数表示点 i−1 到 j−1 的距离(记为 a[i−1,j−1])。
对于任意的 x,y,z,数据保证 a[x,x]=0,a[x,y]=a[y,x] 并且 a[x,y]+a[y,z]≥a[x,z]。
输出格式
输出一个整数,表示最短 Hamilton 路径的长度。
代码:
#include <bits/stdc++.h>
using namespace std;
const int N=21;
int g[N][N];
int f[1<<N][N];
int n;
int main(){
cin>>n;
for(int i=0;i<n;i++)
for(int j=0;j<n;j++)
cin>>g[i][j];
memset(f,0x3f,sizeof f);
f[1][0]=0;
int m=1<<n;
for(int i=0;i<m;i++){//遍历所有集合
for(int j=0;j<n;j++){//从集合中的j
if((1<<j)&i){//j在i中
for(int k=0;k<n;k++){//走到k
if(k!=j&&(1<<k)&i){//j不等于k,并且k在i中
f[i][j]=min(f[i][j],f[i-(1<<j)][k]+g[k][j]);//从k转移过来
}
}
}
}
}
cout<<f[m-1][n-1];
return 0;
}
玉米田:
农夫约翰的土地由 M×NM×N 个小方格组成,现在他要在土地里种植玉米。
非常遗憾,部分土地是不育的,无法种植。
而且,相邻的土地不能同时种植玉米,也就是说种植玉米的所有方格之间都不会有公共边缘。
现在给定土地的大小,请你求出共有多少种种植方法。
土地上什么都不种也算一种方法。
输入格式
第 11 行包含两个整数 MM 和 NN。
第 2..M+12..M+1 行:每行包含 NN 个整数 00 或 11,用来描述整个土地的状况,11 表示该块土地肥沃,00 表示该块土地不育。
输出格式
输出总种植方法对 108108 取模后的值。
代码:
#include<bits/stdc++.h>
using namespace std;
const int mod=1e9;
const int N=15;
int f[N][1<<N];
int n,m;
vector<int> t;
unordered_map<int,vector<int>> e;
int g[N];
int op(int x){
return ((x+mod)%mod+mod)%mod;
}
bool check(int x){//连续的两个不能都是1
if(x&(x<<1))return false;
return true;
}
int main(){
cin>>n>>m;
for(int i=0;i<(1<<m);i++){
if(check(i))t.push_back(i);
}
for(int i:t){
for(int j:t){//和j匹配的i
if((i&j)==0)e[i].push_back(j);
}
}
for(int i=1;i<=n;i++){
for(int j=0;j<m;j++){
int tmp;
cin>>tmp;
if(tmp==0){
g[i]+=(1<<j);
}
}
}//读入状态
f[0][0]=1;
for(int i=1;i<=n+1;i++){
for(int j:t){
if(j&g[i])continue;//没有种在坏地上
for(int k:e[j]){
if(k&g[i-1])continue;//上一行也合法
f[i][j]=op(f[i][j]+f[i-1][k]);
}
}
}
cout<<f[n+1][0];
}
炮兵阵地:
题目描述
司令部的将军们打算在 N×M 的网格地图上部署他们的炮兵部队。
一个 N×M 的地图由 N 行 M 列组成,地图的每一格可能是山地(用 H 表示),也可能是平原(用 P 表示),如下图。
在每一格平原地形上最多可以布置一支炮兵部队(山地上不能够部署炮兵部队);一支炮兵部队在地图上的攻击范围如图中黑色区域所示:

如果在地图中的灰色所标识的平原上部署一支炮兵部队,则图中的黑色的网格表示它能够攻击到的区域:沿横向左右各两格,沿纵向上下各两格。
图上其它白色网格均攻击不到。从图上可见炮兵的攻击范围不受地形的影响。
现在,将军们规划如何部署炮兵部队,在防止误伤的前提下(保证任何两支炮兵部队之间不能互相攻击,即任何一支炮兵部队都不在其他支炮兵部队的攻击范围内),在整个地图区域内最多能够摆放多少我军的炮兵部队。
输入格式
第一行包含两个由空格分割开的正整数,分别表示 N 和 M。
接下来的 N 行,每一行含有连续的 M 个字符,按顺序表示地图中每一行的数据。
输出格式
一行一个整数,表示最多能摆放的炮兵部队的数量。
代码:
#include <bits/stdc++.h>
using namespace std;
const int N=110,M=(1<<10);
int s[N]={0},cnt[M];
int n,m;
int state[M];
int f[2][M][M]={0};
bool check (int st){
for(int i=0;i<10;i++){
if(((st>>i)&1)&&(((st>>(i+1))&1)||((st>>(i+2))&1)))//3个连续的地方只有1个1
return false;
}
return true;
}
int count(int st){
int res=0;
for(int i=0;i<11;i++){
if((st>>i)&1)res++;
}
return res;
}
int main(){
cin>>n>>m;
for(int i=1;i<=n;i++){
for(int j=0;j<m;j++){
char tmp;
cin>>tmp;
if(tmp=='H')
s[i]+=(1<<j);
}
}
int cn=0;
int t=1<<m;
for(int i=0;i<t;i++){//遍历所有的状态
if(check(i)){//i状态合法
state[cn++]=i;//将其加入到state种
cnt[i]=count(i);//同时计算状态中的炮兵数量
}
}
for(int i=1;i<=n+2;i++)//遍历到n+2,最后的答案是n+2行的状态是0
for(int j=0;j<cn;j++)//第i-1行的状态
for(int k=0;k<cn;k++)//第i行的状态
for(int u=0;u<cn;u++){//i-2行的状态
int a=state[k],b=state[j],c=state[u];
if((a&c)||(b&c)||(a&b))continue;//3行里面不能有炮兵重叠
if(s[i]&a||s[i-1]&b)continue;//山地冲突
if(i>=2&&s[i-2]&c)continue;//山地冲突
f[i&1][j][k]=max(f[i&1][j][k],f[i-1&1][u][j]+cnt[a]);
}
cout<<f[n+2&1][0][0];//state[0]对应状态0000000000
}
愤怒的小鸟:
题目背景
NOIP2016 提高组 D2T3
题目描述
Kiana 最近沉迷于一款神奇的游戏无法自拔。
简单来说,这款游戏是在一个平面上进行的。
有一架弹弓位于 (0,0) 处,每次 Kiana 可以用它向第一象限发射一只红色的小鸟,小鸟们的飞行轨迹均为形如 y=ax2+bx 的曲线,其中 a,b 是 Kiana 指定的参数,且必须满足 a<0,a,b 都是实数。
当小鸟落回地面(即 x 轴)时,它就会瞬间消失。
在游戏的某个关卡里,平面的第一象限中有 n 只绿色的小猪,其中第 i 只小猪所在的坐标为 (xi,yi)。
如果某只小鸟的飞行轨迹经过了 (xi,yi),那么第 i 只小猪就会被消灭掉,同时小鸟将会沿着原先的轨迹继续飞行;
如果一只小鸟的飞行轨迹没有经过 (xi,yi),那么这只小鸟飞行的全过程就不会对第 i 只小猪产生任何影响。
例如,若两只小猪分别位于 (1,3) 和 (3,3),Kiana 可以选择发射一只飞行轨迹为 y=−x2+4x 的小鸟,这样两只小猪就会被这只小鸟一起消灭。
而这个游戏的目的,就是通过发射小鸟消灭所有的小猪。
这款神奇游戏的每个关卡对 Kiana 来说都很难,所以 Kiana 还输入了一些神秘的指令,使得自己能更轻松地完成这个游戏。这些指令将在【输入格式】中详述。
假设这款游戏一共有 T 个关卡,现在 Kiana 想知道,对于每一个关卡,至少需要发射多少只小鸟才能消灭所有的小猪。由于她不会算,所以希望由你告诉她。
输入格式
第一行包含一个正整数 T,表示游戏的关卡总数。
下面依次输入这 T 个关卡的信息。每个关卡第一行包含两个非负整数 n,m,分别表示该关卡中的小猪数量和 Kiana 输入的神秘指令类型。接下来的 n 行中,第 i 行包含两个正实数 xi,yi,表示第 i 只小猪坐标为 (xi,yi)。数据保证同一个关卡中不存在两只坐标完全相同的小猪。
如果 m=0,表示 Kiana 输入了一个没有任何作用的指令。
如果 m=1,则这个关卡将会满足:至多用 ⌈n/3+1⌉ 只小鸟即可消灭所有小猪。
如果 m=2,则这个关卡将会满足:一定存在一种最优解,其中有一只小鸟消灭了至少 ⌊n/3⌋ 只小猪。
保证 1≤n≤18,0≤m≤2,0<xi,yi<10,输入中的实数均保留到小数点后两位。
上文中,符号 ⌈c⌉ 和 ⌊c⌋ 分别表示对 c 向上取整和向下取整,例如:⌈2.1⌉=⌈2.9⌉=⌈3.0⌉=⌊3.0⌋=⌊3.1⌋=⌊3.9⌋=3。
输出格式
对每个关卡依次输出一行答案。
输出的每一行包含一个正整数,表示相应的关卡中,消灭所有小猪最少需要的小鸟数量。
代码:
#include<bits/stdc++.h>
using namespace std;
typedef pair<double,double> pdd;
const int N=20;
bool same(double x,double y){
if(fabs(x-y)<1e-6)return 1;
return 0;
}
int t,n,m;
pdd a[N];
int f[N][N];
int g[1<<N];
int main(){
scanf("%d",&t);
while(t--){
cin>>n>>m;
for(int i=0;i<n;i++){
cin>>a[i].first>>a[i].second;
}
memset(f,0,sizeof f);
for(int i=0;i<n;i++){
f[i][i]=1<<i;
for(int j=0;j<n;j++){
if(i==j)continue;
double x1=a[i].first,y1=a[i].second;
double x2=a[j].first,y2=a[j].second;
if(same(x1,x2))continue;
double aa=(y1/x1-y2/x2)/(x1-x2);
if(aa>0)continue;
double bb=y1/x1-aa*x1;
int st=0;
for(int k=0;k<n;k++){
double x=a[k].first,y=a[k].second;
if(same(aa*x*x+bb*x,y)){
st+=1<<k;
}
}
f[i][j]=st;//表示从依据i和j建立的抛物线覆盖的点集合
}
}
memset(g,0x3f,sizeof g);
g[0]=0;
for(int i=0;i<1<<n;i++){
int x=0;
for(int j=0;j<n;j++){//找到没有被覆盖的点
if(i>>j&1){
continue;
}else {
x=j;
break;
}
}
for(int j=0;j<n;j++){
g[i|f[x][j]]=min(g[i|f[x][j]],g[i]+1);
}
}
cout<<g[(1<<n)-1]<<endl;
}
}
明天从区间Dp开始看
