当前位置：首页 > news >正文

scikit-learn在监督学习算法的应用

news 来源：原创 2025/5/4 16:53:57

shiyonguyu大家好，我是我不是小upper！最近行业大环境不是很好，有人苦恼别人都开始着手项目实战了，自己却还卡在 scikit-learn 的代码语法上，连简单的示例运行起来都磕磕绊绊。确实，对很多机器学习初学者来说，一边要啃算法原理，一边得熟悉代码操作，后面还要接触大数据相关知识，每一步都不容易。这也恰恰解释了为什么算法工程师的薪资和待遇普遍比较可观 —— 掌握这些技能需要下不少功夫。

既然大家在 scikit-learn 的学习上遇到困难，接下来这段时间，我就专门和大家唠唠这个工具的使用方法。今天先从监督学习部分入手，其他内容后续也会陆续分享。这篇干货满满，建议先收藏，方便随时拿出来学习！

优缺点

在大家的日常生活中，无论是工作还是学习，scikit-learn都占有举足轻重的地位！咱先聊聊它的优缺点，让大家有一个整体的认识！

优点：

1、简单易用：scikit-learn提供了一种简单而一致的API，使用户能够轻松地训练、评估和部署各种监督学习模型。

2、丰富的文档和示例：详尽的文档和示例，以帮助用户理解算法和如何使用它们，这降低了学习曲线。

3、广泛的算法支持：包括多种监督学习算法，从传统的线性模型到集成方法和深度学习，满足了各种问题的需求。

4、开源社区支持：强大的开源社区，用户可以获得支持、反馈和贡献新功能和改进。

5、性能优化：库中的算法通常经过高度优化，以提供高性能的计算，特别是在大规模数据集上。

6、数据预处理工具：包括数据预处理、特征工程和特征选择工具，有助于准备和处理数据。

7、交叉验证和模型选择：提供了交叉验证和模型选择工具，有助于选择最佳模型参数，避免过拟合。

8、可扩展性：用户可以轻松地扩展库，自定义评估器、转换器和度量。

缺点：

1、有些算法的性能：尽管scikit-learn包括广泛的算法，但某些特殊问题可能需要更专业的库或深度学习框架来实现最佳性能。

2、深度学习支持限制：虽然scikit-learn包括MLP（多层感知机）等神经网络模型，但对于深度学习任务，深度学习框架如TensorFlow和PyTorch可能更适合。

3、自动特征工程：自动特征工程工具有限，复杂的特征工程任务可能需要其他库或手动处理。

4、处理大规模数据集的能力：对于大规模数据集，scikit-learn的性能和内存管理可能存在挑战。

5、不支持序列数据：对于时序数据或自然语言处理任务，需要额外的库和工具。

有了一个整体的认识之后，专门针对监督学习算法，各个举例，给出大家完整可以抛出结果的代码示例来。

线性回归
逻辑回归
支持向量机
决策树和随机森林
K-Means
集成方法
高斯混合模型
梯度提升树
AdaBoost
神经网络

老规矩：大家伙如果觉得近期文章还不错！欢迎大家点赞、转发安排起来，让更多的朋友看到。

线性回归

线性回归的核心目标，是找到一条能最准确描述自变量和因变量之间关系的直线。简单来说，就是通过不断缩小实际数据和预测数据之间的误差，来确定这条最佳的拟合线，进而预测目标变量的值。比如在房价预测场景中，我们想知道房屋的某个特征（像房间数量）和房价之间存在怎样的线性关系，这就是线性回归可以解决的问题。

接下来，我们通过一个波士顿房价预测的案例，详细展示线性回归的完整实现流程，整个过程包括数据准备、模型构建、训练、预测、评估以及可视化六个关键步骤。

1. 导入必要的库

在开始编写代码之前，我们需要先导入一些重要的工具库。

numpy：强大的数值计算库，用于处理各种数据运算。
matplotlib.pyplot：绘图库，能帮我们将数据和模型结果以可视化的形式展示出来，方便直观理解。
sklearn 相关模块：sklearn 是机器学习领域常用的库，其中 datasets 模块用来加载公开数据集；linear_model 里的 LinearRegression 用于构建线性回归模型；model_selection 中的 train_test_split 负责将数据集拆分为训练集和测试集；metrics 模块里的 mean_squared_error 和 r2_score 则用于评估模型的性能。

具体代码如下：

import numpy as np
import matplotlib.pyplot as plt
from sklearn import datasets
from sklearn.linear_model import LinearRegression
from sklearn.model_selection import train_test_split
from sklearn.metrics import mean_squared_error, r2_score

2. 加载和准备数据

我们使用经典的波士顿房价数据集，这个数据集包含了房屋的多种特征以及对应的房价信息。为了简化演示过程，这里我们只选取 “平均房间数” 这一个特征作为自变量，来预测房屋价格（因变量）。

# 加载波士顿房价数据集
boston = datasets.load_boston()
# 准备数据，选取房间数作为特征
X = boston.data[:, np.newaxis, 5]
# 目标变量，即房屋价格
y = boston.target

3. 划分数据集

为了准确评估模型在新数据上的表现，我们需要把数据集分成两部分：一部分用于训练模型，让模型学习特征和目标变量之间的关系；另一部分用于测试模型，检验模型的泛化能力。

这里我们将数据集的 80% 作为训练集，20% 作为测试集，并且设置 random_state=42，这样可以保证每次运行代码时，数据集的划分结果都是一样的，方便对比和调试。

# 划分训练集和测试集
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)

4. 构建和训练模型

接下来，我们创建一个线性回归模型对象，并使用训练集数据对其进行训练。训练的过程，就是模型根据给定的特征和目标值，不断调整自身参数，寻找最佳拟合线的过程。

# 构建线性回归模型
model = LinearRegression()
# 训练模型
model.fit(X_train, y_train)

5. 进行预测

模型训练好之后，我们就可以用它来对测试集中的数据进行预测，得到每个样本对应的预测房价。

# 进行预测
y_pred = model.predict(X_test)

6. 评估模型性能

为了衡量模型预测的准确性，我们使用两个常用的评估指标：

均方误差（MSE）：计算预测值和实际值之间差值的平方的平均值，MSE 值越小，说明模型的预测越准确。
决定系数（R²）：用于评估模型对数据的拟合程度，取值范围在 0 到 1 之间，越接近 1 表示模型拟合效果越好。

# 评估模型
mse = mean_squared_error(y_test, y_pred)
r2 = r2_score(y_test, y_pred)

7. 可视化结果

最后，我们通过绘图的方式，直观展示模型的拟合效果。将测试集中的实际数据点绘制出来，再把模型预测的拟合线画在同一图中，这样就能清晰地看到模型预测值和实际值的差异。

# 可视化结果
plt.scatter(X_test, y_test, color='black', label='实际数据')
plt.plot(X_test, y_pred, color='blue', linewidth=3, label='线性回归拟合')
plt.title('线性回归预测房价')
plt.xlabel('平均房间数')
plt.ylabel('房屋价格')
plt.legend()
plt.show()

运行完代码后，我们还可以打印出评估指标的具体数值，进一步了解模型的性能表现：

print(f"均方误差(Mean Squared Error): {mse:.2f}")
print(f"决定系数(R^2): {r2:.2f}")

逻辑回归

通过 Scikit - Learn 中的 Iris 数据集进行一个具体的二元分类实践。

逻辑回归虽然名字里有 “回归”，但它主要用于解决分类问题。它的核心是找到一个决策边界，把不同类别的数据点区分开来。就像在一个大广场上画一条线，让不同阵营的人分别站在线的两边。

1. 导入必要的库

在开始代码编写之前，我们得先把要用的工具准备好，也就是导入相关的库：

numpy：它在处理数值计算方面超厉害，能帮我们高效地操作和处理数据。
matplotlib.pyplot：这个库主要用来绘图。通过它，我们可以把数据和模型的结果用图形展示出来，这样就能更直观地理解。
sklearn 相关模块：sklearn 是机器学习领域特别常用的库。这里面的 datasets 模块可以帮我们加载公开的数据集，像我们要用的 Iris 数据集就靠它；linear_model 里的 LogisticRegression 就是我们构建逻辑回归模型要用到的类。

具体导入代码如下：

import numpy as np
import matplotlib.pyplot as plt
from sklearn import datasets
from sklearn.linear_model import LogisticRegression

2. 加载和处理 Iris 数据集

Iris 数据集包含了三种不同种类鸢尾花的测量数据。为了方便后续可视化，我们只选择其中两个特征，也就是萼片长度和萼片宽度。同时，我们把原本多分类的标签转化成一个二元分类问题，规定其中一种鸢尾花对应的标签为 0，另一种为 1 。

代码实现是这样的：

# 加载Iris数据集
iris = datasets.load_iris()
# 仅使用前两个特征（萼片长度和萼片宽度），方便可视化
X = iris.data[:, :2]
# 将标签转换为二进制分类问题，不是0类的就标记为1
y = (iris.target != 0) * 1

3. 构建和训练逻辑回归模型

接下来，我们要创建一个逻辑回归模型对象。这里我们指定了求解器为 liblinear，它适用于小规模数据集，能比较高效地找到模型的最优参数。然后，我们用准备好的数据集对模型进行训练，让模型学习数据中蕴含的规律，找到能区分两类鸢尾花的决策边界。

代码如下：

# 构建逻辑回归模型
model = LogisticRegression(solver='liblinear')
# 训练模型
model.fit(X, y)

4. 绘制决策边界图

模型训练好之后，我们想看看它找到的决策边界长啥样，以及数据点在这个边界两边是怎么分布的，这就需要绘制决策边界图。
我们先确定绘图区域的范围，也就是找到特征数据在两个维度上的最小值和最大值，然后向外扩展一点，保证能把所有数据点都包含进去。接着，我们创建一个网格，这个网格就像是在绘图区域铺上了密密麻麻的小方格。对于网格中的每个点，我们用训练好的模型去预测它属于哪一类，得到预测结果后，把这些结果按照网格的形状重新排列。最后，我们把决策边界和数据点都画出来。

具体代码如下：

# 确定绘图区域范围
x_min, x_max = X[:, 0].min() - 0.5, X[:, 0].max() + 0.5
y_min, y_max = X[:, 1].min() - 0.5, X[:, 1].max() + 0.5
# 创建网格
xx, yy = np.meshgrid(np.arange(x_min, x_max, 0.01), np.arange(y_min, y_max, 0.01))
# 对网格中的点进行预测
Z = model.predict(np.c_[xx.ravel(), yy.ravel()])
Z = Z.reshape(xx.shape)plt.contourf(xx, yy, Z, alpha=0.8)
plt.scatter(X[:, 0], X[:, 1], c=y, edgecolor='k')
plt.xlabel('Sepal Length')
plt.ylabel('Sepal Width')
plt.title('LogisticRegression')
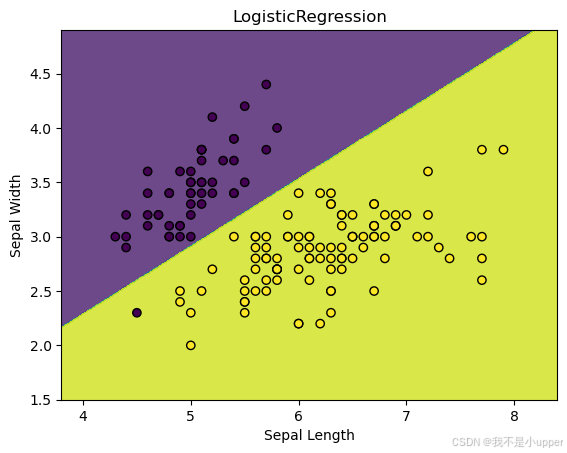
plt.show()

运行这段代码，我们就能看到逻辑回归模型找到的那条分隔两种鸢尾花的决策边界，以及数据点在边界两侧的分布情况。下图很好地展示了逻辑回归用于二元分类问题的关键概念，也就是如何通过找到合适的决策边界来区分不同类别的数据。希望大家通过这个例子，能对逻辑回归有更深入的理解！

支持向量机在新颖性检测中的应用

在实际的数据处理场景中，新颖性检测是一项非常重要的任务，它能够帮助我们识别出数据中的异常情况。下面，我们将使用 Scikit - Learn 中的支持向量机（SVM）模型来完成一个新颖性检测的案例。这个案例会详细展示从准备数据、构建模型到可视化结果的整个过程，让大家更清晰地理解支持向量机在新颖性检测中的工作原理。

1. 导入必要的库

在开始之前，我们需要导入一些必要的 Python 库，这些库将帮助我们完成数据生成、模型构建和结果可视化等任务。

import matplotlib.pyplot as plt
import numpy as np
from sklearn import svm

这里，numpy 库用于进行数值计算和数据生成，matplotlib.pyplot 库用于绘制图形，sklearn 中的 svm 模块则提供了支持向量机模型。

2. 生成合成数据集

为了演示新颖性检测，我们需要创建一个包含正常观测和异常观测的合成数据集。我们使用 numpy 的随机数生成功能来完成这个任务。

# 设置随机数种子，保证结果可复现
np.random.seed(0)
# 生成训练集中的正常观测数据
X = 0.3 * np.random.randn(100, 2)
X_train = np.r_[X + 2, X - 2]
# 生成测试集中的正常观测数据
X = 0.3 * np.random.randn(20, 2)
X_test = np.r_[X + 2, X - 2]
# 生成异常观测数据
X_outliers = np.random.uniform(low=-4, high=4, size=(20, 2))

在这段代码中，我们首先设置了随机数种子，这样每次运行代码时生成的数据都是一样的，方便结果的复现。然后，我们通过 np.random.randn 函数生成符合正态分布的随机数，构建训练集和测试集中的正常观测数据。最后，使用 np.random.uniform 函数生成均匀分布的随机数作为异常观测数据。

3. 构建支持向量机模型

接下来，我们使用 sklearn 中的 OneClassSVM 模型进行新颖性检测。OneClassSVM 是一种无监督学习模型，它只需要正常数据作为输入，然后学习正常数据的分布特征，从而识别出异常数据。

# 构建支持向量机模型
clf = svm.OneClassSVM(nu=0.1, kernel="rbf", gamma=0.1)
# 使用训练数据拟合模型
clf.fit(X_train)

在创建模型时，我们设置了一些参数。nu 表示异常数据在整个数据集中所占的比例上限，kernel 选择了径向基函数（RBF）作为核函数，gamma 是核函数的系数，它会影响模型的复杂度和泛化能力。然后，我们使用训练数据 X_train 对模型进行训练。

4. 进行预测并统计错误数量

模型训练好后，我们使用它对训练数据、测试数据和异常数据进行预测，并统计预测错误的数量。

# 对训练数据进行预测
y_pred_train = clf.predict(X_train)
# 对测试数据进行预测
y_pred_test = clf.predict(X_test)
# 对异常数据进行预测
y_pred_outliers = clf.predict(X_outliers)# 统计训练数据中的预测错误数量
n_error_train = y_pred_train[y_pred_train == -1].size
# 统计测试数据中的预测错误数量
n_error_test = y_pred_test[y_pred_test == -1].size
# 统计异常数据中的预测错误数量
n_error_outliers = y_pred_outliers[y_pred_outliers == 1].size

在 OneClassSVM 模型中，预测结果为 1 表示正常数据，-1 表示异常数据。我们通过比较预测结果和实际情况，统计出不同数据集上的预测错误数量。

5. 可视化结果

为了更直观地展示支持向量机模型的工作效果，我们使用 matplotlib 库绘制图形。

# 创建网格点
xx, yy = np.meshgrid(np.linspace(-5, 5, 500), np.linspace(-5, 5, 500))
# 计算网格点到决策边界的距离
Z = clf.decision_function(np.c_[xx.ravel(), yy.ravel()])
Z = Z.reshape(xx.shape)# 设置图形标题
plt.title("Novelty Detection")
# 绘制决策边界以下的区域
plt.contourf(xx, yy, Z, levels=np.linspace(Z.min(), 0, 7), cmap=plt.cm.PuBu)
# 绘制决策边界
a = plt.contour(xx, yy, Z, levels=[0], linewidths=2, colors="darkred")
# 绘制决策边界以上的区域
plt.contourf(xx, yy, Z, levels=[0, Z.max()], colors="palevioletred")# 设置散点大小
s = 40
# 绘制训练数据点
b1 = plt.scatter(X_train[:, 0], X_train[:, 1], c="white", s=s, edgecolors="k")
# 绘制测试数据点
b2 = plt.scatter(X_test[:, 0], X_test[:, 1], c="blueviolet", s=s, edgecolors="k")
# 绘制异常数据点
c = plt.scatter(X_outliers[:, 0], X_outliers[:, 1], c="gold", s=s, edgecolors="k")
# 设置坐标轴范围
plt.axis("tight")
plt.xlim((-5, 5))
plt.ylim((-5, 5))
# 添加图例
plt.legend([a.collections[0], b1, b2, c],["Learned Frontier","Training Observations","New Regular Observations","New Abnormal Observations",],loc="upper left",prop=plt.matplotlib.font_manager.FontProperties(size=11),
)
# 添加x轴标签，显示预测错误数量
plt.xlabel("Train Errors: %d/200 ; Novel Regular Errors: %d/40 ; Novel Abnormal Errors: %d/40"% (n_error_train, n_error_test, n_error_outliers)
)
# 显示图形
plt.show()

我们创建了一个包含正常观测和异常观测的合成数据集，并使用 OneClassSVM 模型进行新颖性检测。模型通过学习正常数据的分布特征，找到了一个决策边界，将正常观测和异常观测分开。通过可视化结果，我们可以清晰地看到支持向量机是如何找到这个学习边界的，这也充分演示了支持向量机在异常检测问题中的应用。大家可以根据自己的需求调整模型的参数，进一步优化模型的性能。

决策树与随机森林

在机器学习领域，决策树和随机森林是两种非常重要且常用的分类模型。今天，我们通过一个具体的案例，使用 Scikit - Learn 中的 Iris 数据集，来深入了解这两种模型的工作原理，并通过可视化它们的决策边界，直观感受它们是如何对数据进行分类的。

1. 导入必要的库

在开始编写代码之前，我们要先把需要用到的库导入进来。这些库就像是我们进行机器学习实验的工具包，能帮助我们完成数据加载、模型训练、结果可视化等一系列操作。

import matplotlib.pyplot as plt
import numpy as np
from sklearn.datasets import load_iris
from sklearn.inspection import DecisionBoundaryDisplay
from sklearn.tree import DecisionTreeClassifier
from sklearn.ensemble import RandomForestClassifier

这里，matplotlib.pyplot 用于绘制图形，numpy 用于数值计算，load_iris 函数可以帮我们加载 Iris 数据集，DecisionBoundaryDisplay 用于可视化模型的决策边界，DecisionTreeClassifier 是决策树模型的类，RandomForestClassifier 则是随机森林模型的类。

2. 加载 Iris 数据集

Iris 数据集是一个非常经典的机器学习数据集，它包含了三种不同种类鸢尾花的多种特征数据以及对应的类别标签。我们通过下面的代码来加载这个数据集：

iris = load_iris()

加载完成后，iris 这个变量就包含了所有的花的特征数据和类别信息，我们后续的模型训练和分析都将基于这些数据。

3. 设置一些参数

在进行模型训练和可视化之前，我们先设置一些参数，方便后续的操作和图形展示。

n_classes = 3
plot_colors = "ryb"
plot_step = 0.02

n_classes 表示 Iris 数据集中花的类别数量，这里是 3 种。plot_colors 定义了用于绘制不同类别数据点的颜色，分别对应红（r）、黄（y）、蓝（b）三种颜色。plot_step 是在绘制决策边界时，网格点之间的间隔大小。

4. 创建图形并划分区域

为了同时展示不同特征组合下决策树和随机森林模型的决策边界，我们创建一个包含 2x2 子图的图形。

fig, sub = plt.subplots(2, 2)
plt.subplots_adjust(wspace=0.4, hspace=0.4)

这样，我们就有了 4 个小的绘图区域，可以分别用来绘制不同特征组合下的模型决策边界和数据点分布。plt.subplots_adjust 函数调整了子图之间的水平和垂直间距，让图形看起来更美观、布局更合理。

5. 训练模型并绘制决策边界

接下来，是整个案例的核心部分。我们要对不同的特征组合，分别训练决策树模型和随机森林模型，并绘制它们的决策边界。

for pairidx, pair in enumerate([[0, 1], [0, 2], [0, 3], [1, 2]]):X = iris.data[:, pair]y = iris.target# 训练决策树模型clf_tree = DecisionTreeClassifier().fit(X, y)# 训练随机森林模型clf_rf = RandomForestClassifier(n_estimators=100, random_state=42).fit(X, y)# 绘制决策边界ax = sub[pairidx // 2, pairidx % 2]DecisionBoundaryDisplay.from_estimator(clf_tree,X,cmap=plt.cm.RdYlBu,response_method="predict",ax=ax,xlabel=iris.feature_names[pair[0]],ylabel=iris.feature_names[pair[1]],)ax.set_title("Decision Tree")DecisionBoundaryDisplay.from_estimator(clf_rf,X,cmap=plt.cm.RdYlBu,response_method="predict",ax=ax,xlabel=iris.feature_names[pair[0]],ylabel=iris.feature_names[pair[1]],)ax.set_title("Random Forest")

在这个循环中，我们依次选取不同的特征组合（比如花瓣长度和花瓣宽度、萼片长度和花瓣长度等）。对于每一组特征，我们先提取对应的特征数据 X 和类别标签 y，然后分别创建并训练一个决策树模型 clf_tree 和一个随机森林模型 clf_rf。随机森林模型中，我们设置了 n_estimators=100，表示由 100 棵决策树组成森林，random_state=42 是为了保证每次运行代码时，模型的随机性是一致的，结果可复现。

训练好模型后，我们使用 DecisionBoundaryDisplay.from_estimator 函数分别绘制决策树和随机森林模型的决策边界。在绘制时，我们指定了颜色映射 cmap=plt.cm.RdYlBu，这样不同区域会根据模型的预测结果显示不同颜色，方便我们区分。同时，我们给每个子图设置了标题，标明是决策树还是随机森林的决策边界。

6. 绘制训练数据点

在绘制完决策边界后，我们还要把训练数据点绘制到图上，用不同颜色表示不同的类别，这样可以更直观地看到模型的分类效果。

for i, color in zip(range(n_classes), plot_colors):idx = np.where(y == i)ax.scatter(X[idx, 0],X[idx, 1],c=color,label=iris.target_names[i],cmap=plt.cm.RdYlBu,edgecolor="black",s=15,)

这段代码遍历每个类别，找到属于该类别的数据点索引 idx，然后使用 ax.scatter 函数将这些数据点以散点的形式绘制在对应的子图上，并且设置了颜色、标签等属性。

7. 添加标题和图例

最后，我们给整个图形添加一个总标题，并且添加图例，方便我们理解图中不同颜色和区域代表的含义。

plt.suptitle("Decision Surface of Decision Trees and Random Forest on Pairs of Features")
plt.legend(loc="lower right", borderpad=0, handletextpad=0)
plt.axis("tight")
plt.show()

plt.suptitle 函数添加了总标题，说明了图中展示的是决策树和随机森林在不同特征组合下的决策表面。plt.legend 函数添加了图例，指定了图例的位置在右下角等属性。plt.axis("tight") 调整了坐标轴的范围，让图形展示更紧凑。最后 plt.show() 显示出整个图形。

通过这个案例，我们可以清楚地看到决策树和随机森林的决策边界，以及它们在 Iris 数据集不同特征组合下是如何进行分类的。这有助于我们深入理解这两种模型的本质，以及它们处理数据和进行分类的方式。希望大家通过这个例子，能对决策树和随机森林模型有更深刻的认识！

K-Means 聚类

我们通过一个具体的例子来学习 K-Means 聚类算法。K-Means 聚类是一种无监督学习方法，主要用于将数据点划分成不同的簇，帮助我们理解数据内在的结构。

首先，我们使用 Scikit - Learn 中的工具来生成一个合成数据集。我们调用 make_blobs 函数，设定生成 1000 个数据点，每个数据点有 2 个特征，并且将这些数据点自然地分成 4 个簇，同时设置随机数种子为 42，这样每次运行代码得到的数据集都是一样的，方便我们进行调试和对比。代码如下：

import matplotlib.pyplot as plt
from sklearn.cluster import KMeans
from sklearn.datasets import make_blobsn_samples = 1000
n_features = 2
n_clusters = 4
random_state = 42
X, _ = make_blobs(n_samples=n_samples, n_features=n_features, centers=n_clusters, random_state=random_state)

生成数据集后，我们开始构建 K-Means 模型。我们创建一个 KMeans 对象，指定要将数据分成 4 个簇，同样设置随机数种子为 42，以保证模型初始化的随机性一致。代码是：

kmeans = KMeans(n_clusters=n_clusters, random_state=random_state)

接下来，我们用生成的数据 X 来训练这个 K-Means 模型，让模型学习数据的分布特征，找到合适的簇划分方式。训练代码为：

kmeans.fit(X)

模型训练完成后，我们可以获取两个重要的结果。一个是簇中心，也就是每个簇的中心点坐标，它代表了这个簇数据点的平均特征位置；另一个是每个数据点所属的簇的标签，通过这个标签我们能知道每个数据点被划分到了哪个簇。获取这两个结果的代码如下：

cluster_centers = kmeans.cluster_centers_
labels = kmeans.labels_

最后，为了更直观地看到 K-Means 聚类的效果，我们使用 matplotlib 库来绘制图形。我们把所有的数据点绘制出来，根据它们所属的簇用不同颜色表示，这样可以很清楚地看到不同簇的数据点分布情况。同时，我们用红色的 “X” 标记出每个簇的中心位置。绘制图形的代码如下：

plt.figure(figsize=(8, 6))
plt.scatter(X[:, 0], X[:, 1], c=labels, cmap='viridis', s=50, alpha=0.7)
plt.scatter(cluster_centers[:, 0], cluster_centers[:, 1], c='red', s=200, marker='X', label='Cluster Centers')
plt.title('K-Means Clustering')
plt.xlabel('Feature 1')
plt.ylabel('Feature 2')
plt.legend()
plt.show()

上图展示了 K-Means 聚类是如何将数据点分成不同的簇的。通过这个例子，我们可以更好地理解 K-Means 聚类的本质，即通过寻找合适的簇中心，将数据点划分到不同的簇中，从而揭示数据的结构特征。希望大家通过这个案例，能对 K-Means 聚类算法有更深入的认识！

集成方法实战

集成方法的核心思路是把多个模型组合起来，发挥它们的优势，从而获得比单个模型更好的性能。我们会使用 Scikit-Learn 库创建一个合成数据集，并运用RandomTreesEmbedding和ExtraTreesClassifier两种方法，来展示集成方法的具体应用和效果。

1. 生成合成数据集

首先，我们用make_circles函数创建一个合成数据集。这个数据集由两类数据点组成，形状类似两个同心圆，参数factor=0.5控制两个圆的距离，noise=0.05给数据添加一些随机噪声，让数据更接近真实情况，random_state=0保证每次运行代码生成的数据都一样。代码如下：

import matplotlib.pyplot as plt
import numpy as np
from sklearn.datasets import make_circles
from sklearn.decomposition import TruncatedSVD
from sklearn.ensemble import ExtraTreesClassifier, RandomTreesEmbedding
from sklearn.naive_bayes import BernoulliNBX, y = make_circles(factor=0.5, random_state=0, noise=0.05)

这里X存储的是数据点的特征，每个数据点有 2 个特征；y是数据点的类别标签，用来表示每个数据点属于哪一类。

2. 使用 RandomTreesEmbedding 转换数据

接下来，我们用RandomTreesEmbedding对数据进行转换。这个方法通过构建多棵决策树，把原始数据映射到一个新的特征空间。我们设置使用 10 棵树（n_estimators=10），树的最大深度为 3（max_depth=3），并固定随机种子（random_state=0），让结果可重复。转换后的数据X_transformed，特征数量会比原始数据多很多。

hasher = RandomTreesEmbedding(n_estimators=10, random_state=0, max_depth=3)
X_transformed = hasher.fit_transform(X)

3. 数据降维以便可视化

由于X_transformed特征太多，不方便直接可视化，我们用TruncatedSVD进行降维，把数据从高维降到 2 维，这样就能在平面上画图展示了。

svd = TruncatedSVD(n_components=2)
X_reduced = svd.fit_transform(X_transformed)

4. 训练朴素贝叶斯分类器

降维后，我们用BernoulliNB训练一个朴素贝叶斯分类器。朴素贝叶斯基于概率来预测数据的类别，我们用转换后的数据X_transformed和对应的标签y来训练它，让它学习数据的分类规律。

nb = BernoulliNB()
nb.fit(X_transformed, y)

5. 训练 ExtraTreesClassifier

同时，我们用ExtraTreesClassifier也训练一个模型，用来和前面的方法做对比。这个模型和随机森林类似，也是由多棵决策树组成，但在构建树的过程中有一些不同，能提高模型的性能。我们设置树的最大深度为 3，使用 10 棵树，同样固定随机种子。

trees = ExtraTreesClassifier(max_depth=3, n_estimators=10, random_state=0)
trees.fit(X, y)

6. 可视化展示

为了直观地看到不同方法的效果，我们绘制了 4 个子图：

原始数据图：展示最初生成的合成数据，能看到两类数据点像两个套在一起的圆圈分布。

ax = plt.subplot(221)
ax.scatter(X[:, 0], X[:, 1], c=y, s=50, edgecolor="k")
ax.set_title("Original Data (2d)")
ax.set_xticks(())
ax.set_yticks(())

2. 降维后的数据图：展示RandomTreesEmbedding转换并经TruncatedSVD降维后的数据分布，能看到数据在新的 2 维空间中的样子。

ax = plt.subplot(222)
ax.scatter(X_reduced[:, 0], X_reduced[:, 1], c=y, s=50, edgecolor="k")
ax.set_title("Truncated SVD reduction (2d) of transformed data (%dd)" % X_transformed.shape[1]
)
ax.set_xticks(())
ax.set_yticks(())

3. 转换数据后的朴素贝叶斯分类结果图：在原始数据空间中，用RandomTreesEmbedding转换网格数据，再用朴素贝叶斯预测每个网格点属于某一类的概率，通过颜色深浅展示预测结果，叠加原始数据点，能看到模型划分的决策边界。

h = 0.01
x_min, x_max = X[:, 0].min() - 0.5, X[:, 0].max() + 0.5
y_min, y_max = X[:, 1].min() - 0.5, X[:, 1].max() + 0.5
xx, yy = np.meshgrid(np.arange(x_min, x_max, h), np.arange(y_min, y_max, h))transformed_grid = hasher.transform(np.c_[xx.ravel(), yy.ravel()])
y_grid_pred = nb.predict_proba(transformed_grid)[:, 1]ax = plt.subplot(223)
ax.set_title("Naive Bayes on Transformed data")
ax.pcolormesh(xx, yy, y_grid_pred.reshape(xx.shape))
ax.scatter(X[:, 0], X[:, 1,], c=y, s=50, edgecolor="k")
ax.set_ylim(-1.4, 1.4)
ax.set_xlim(-1.4, 1.4)
ax.set_xticks(())
ax.set_yticks(())

4. ExtraTreesClassifier 分类结果图：同样在原始数据空间，用ExtraTreesClassifier预测每个网格点属于某一类的概率，展示决策边界和原始数据点，对比两种方法的分类效果。

y_grid_pred = trees.predict_proba(np.c_[xx.ravel(), yy.ravel()])[:, 1]ax = plt.subplot(224)
ax.set_title("ExtraTrees predictions")
ax.pcolormesh(xx, yy, y_grid_pred.reshape(xx.shape))
ax.scatter(X[:, 0], X[:, 1], c=y, s=50, edgecolor="k")
ax.set_ylim(-1.4, 1.4)
ax.set_xlim(-1.4, 1.4)
ax.set_xticks(())
ax.set_yticks(())

最后，我们调整子图布局，让整个图表看起来更协调，并显示图表。

plt.tight_layout()
plt.show()

通过这个案例，我们知道了如何使用RandomTreesEmbedding和ExtraTreesClassifier这两种集成方法处理数据，还通过可视化，直观地看到了不同方法划分的决策边界和分类效果。这能帮助我们更好地理解集成方法的工作原理，以及组合多个模型是如何提升整体性能的。如果在学习过程中有任何疑问，欢迎一起讨论！

高斯混合模型（GMM）实战

大家好！今天我们来学习高斯混合模型（Gaussian Mixture Model，简称 GMM），这是一个在聚类和密度估计方面非常有用的概率模型。GMM 的基本思路是，假设我们的数据是由多个高斯分布（也就是常见的正态分布，像钟形曲线那样）混合而成的，每个高斯分布就代表一个聚类。接下来，我们用 Scikit - Learn 库中的GaussianMixture类，结合经典的 Iris 数据集，手把手教大家如何构建和可视化 GMM 模型。

1. 准备数据

我们使用 Scikit - Learn 内置的 Iris 数据集，这个数据集很经典，包含了三种不同种类鸢尾花的特征测量数据。具体来说，每个鸢尾花样本都有四个特征：花萼长度、花萼宽度、花瓣长度和花瓣宽度。我们通过下面的代码加载数据集：

import matplotlib.pyplot as plt
import numpy as np
from sklearn import datasets
from sklearn.mixture import GaussianMixture
from sklearn.decomposition import PCA
from sklearn import datasets
iris = datasets.load_iris()
X = iris.data
y = iris.target

这里，X是一个二维数组，每一行代表一个鸢尾花样本，每一列对应一个特征；y是样本的真实类别标签，不过在聚类任务里，我们一开始不会用到它，主要用X里的特征数据来做聚类。

2. 构建和训练 GMM 模型

接下来，我们创建 GMM 模型。因为 Iris 数据集里有三种鸢尾花，所以我们设定聚类数量为 3，也就是让模型把数据分成 3 个簇。

from sklearn.mixture import GaussianMixture
n_components = 3  # 聚类数量设为3
gmm = GaussianMixture(n_components=n_components)

创建好模型后，我们用数据X来训练它，让模型自己去估计每个高斯分布的参数，比如均值（可以理解为每个簇的中心位置）和协方差矩阵（描述特征之间的相关性和数据的分散程度）。

gmm.fit(X)

3. 进行预测和获取概率

模型训练好后，我们可以做两件事：

预测聚类标签：让模型判断每个样本属于哪个聚类，得到每个样本的聚类标签。

labels = gmm.predict(X)

获取概率：除了知道样本属于哪个聚类，我们还能知道每个样本属于每个聚类的概率，这是 GMM 很独特的地方。

probs = gmm.predict_proba(X)

4. 数据降维以便可视化

由于原始数据有四个特征，很难直接在平面上画出来展示。所以我们用主成分分析（PCA）把数据降到 2 维，这样就能在一张图上直观地看到聚类效果了。

from sklearn.decomposition import PCA
pca = PCA(n_components=2)
X_reduced = pca.fit_transform(X)

5. 绘制可视化结果

我们绘制两张图来展示 GMM 的聚类效果：

左边的图：根据预测的聚类标签，把数据点画出来，不同标签的数据点用不同颜色表示。这样一眼就能看出模型把数据分成了哪几个簇。

plt.figure(figsize=(12, 6))
plt.subplot(1, 2, 1)
plt.scatter(X_reduced[:, 0], X_reduced[:, 1], c=labels, cmap='viridis')
plt.title('GMM Clustering')
plt.xlabel('First Principal Component')
plt.ylabel('Second Principal Component')

右边的图：根据每个样本属于每个聚类的概率来画图，概率越高，颜色越深。通过这张图，我们能看到每个数据点和不同聚类之间的 “亲密程度”，也就是属于某个聚类的可能性大小。

plt.subplot(1, 2, 2)
plt.scatter(X_reduced[:, 0], X_reduced[:, 1], c=probs, cmap='viridis', marker='x')
plt.title('GMM Clustering (Probabilities)')
plt.xlabel('First Principal Component')
plt.ylabel('Second Principal Component')
plt.show()

通过这个案例，我们完整地演示了如何用 GMM 对 Iris 数据集进行聚类，从数据准备、模型构建，到最后的可视化展示。上图看到了 GMM 把数据分成了哪些簇，可以看出每个样本属于不同簇的概率情况。GMM 是一个很强大的聚类算法，尤其适合数据呈现多种分布的情况。如果在学习过程中有任何疑问，欢迎一起交流讨论！

梯度提升树实战

梯度提升树（Gradient Boosting）算法，这是一种非常强大的集成学习方法，通过不断叠加多个决策树，逐步提升模型的预测能力。我们会用 Scikit-Learn 库中的GradientBoostingClassifier，通过实际案例演示如何用它解决分类问题，还会对比带提前停止机制的版本，看看优化后的效果。

1. 准备数据

我们选用 Scikit-Learn 内置的三个不同数据集：

Iris 数据集：经典的花卉分类数据，包含三种鸢尾花的花萼、花瓣等特征，用来预测花的种类。
随机生成的分类数据集：用make_classification函数生成 800 个样本数据，适合测试模型在常规分类任务中的表现。
Hastie 数据集：用make_hastie_10_2函数生成 2000 个样本，数据分布更复杂，能考验模型处理复杂问题的能力。

import time
import matplotlib.pyplot as plt
import numpy as np
from sklearn import datasets, ensemble
from sklearn.model_selection import train_test_split# 数据集和名称
data_list = [datasets.load_iris(return_X_y=True),datasets.make_classification(n_samples=800, random_state=0),datasets.make_hastie_10_2(n_samples=2000, random_state=0),
]
names = ["Iris Data", "Classification Data", "Hastie Data"]

这里data_list存储加载后的数据集，每个数据集包含特征数据X和对应的标签y；names记录数据集的名称，方便后续展示。

2. 构建和训练模型

我们要构建两种梯度提升树模型：

普通梯度提升树：用GradientBoostingClassifier创建，设定使用 200 棵决策树（n_estimators=200），让模型逐步叠加这些树来优化预测效果。
带提前停止机制的梯度提升树：同样基于GradientBoostingClassifier，除了设置 200 棵树，还添加了提前停止参数。validation_fraction=0.2表示从训练数据中拿出 20% 作为验证集，n_iter_no_change=5和tol=0.01组合起来表示，如果连续 5 次迭代中，验证集上的损失降低幅度小于 0.01，就停止训练，避免模型过拟合。

# 初始化列表用于存储结果
n_gb = []
score_gb = []
time_gb = []
n_gbes = []
score_gbes = []
time_gbes = []n_estimators = 200for X, y in data_list:X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=0)# 创建梯度提升树模型gbes = ensemble.GradientBoostingClassifier(n_estimators=n_estimators,validation_fraction=0.2,n_iter_no_change=5,tol=0.01,random_state=0,)gb = ensemble.GradientBoostingClassifier(n_estimators=n_estimators, random_state=0)# 训练并记录时间start = time.time()gb.fit(X_train, y_train)time_gb.append(time.time() - start)start = time.time()gbes.fit(X_train, y_train)time_gbes.append(time.time() - start)

在循环中，我们对每个数据集都做同样的操作：先把数据拆成 80% 的训练集和 20% 的测试集；然后分别训练两种模型，记录每个模型的训练时间。

3. 评估模型并记录结果

训练完成后，我们用测试集评估模型的表现：

计算准确率：用score方法计算模型在测试集上的分类准确率，数值越高说明模型预测得越准。
记录迭代次数：对于带提前停止机制的模型，查看实际训练了多少棵树就停止了，和普通模型固定的 200 棵树做对比。

    # 计算准确度并记录score_gb.append(gb.score(X_test, y_test))score_gbes.append(gbes.score(X_test, y_test))# 记录训练的迭代次数n_gb.append(gb.n_estimators_)n_gbes.append(gbes.n_estimators_)

4. 可视化对比结果

最后，我们用 Matplotlib 绘制柱状图，直观对比两种模型在不同数据集上的表现：

# 绘制图形
bar_width = 0.2
n = len(data_list)
index = np.arange(0, n * bar_width, bar_width) * 2.5
index = index[0:n]plt.figure(figsize=(10, 6))
plt.bar(index, score_gb, bar_width, label='Gradient Boosting', color='b', alpha=0.7)
plt.bar(index + bar_width, score_gbes, bar_width, label='Gradient Boosting with Early Stopping', color='g', alpha=0.7)
plt.xlabel('Dataset')
plt.ylabel('Accuracy')
plt.title('Accuracy of Gradient Boosting vs. Early Stopping Gradient Boosting')
plt.xticks(index + bar_width, names)
plt.legend(loc='best')
plt.tight_layout()
plt.show()

图中蓝色柱子代表普通梯度提升树模型的准确率，绿色柱子代表带提前停止机制的模型准确率。横轴是不同的数据集名称，纵轴是准确率数值。通过这张图，我们能清楚看到：在不同复杂度的数据上，两种模型的表现有什么差异，提前停止机制是否真的能提升模型性能、减少训练时间。

通过这个案例，我们完整展示了梯度提升树解决分类问题的全流程，还对比了优化后的模型效果。梯度提升树不仅能用于分类，解决回归问题也很出色，在实际的数据分析和机器学习项目中应用非常广泛。如果对代码或原理有疑问，欢迎随时交流！

AdaBoost 实战

AdaBoost 算法在回归任务中的应用。想象一下，我们手头有一组数据，这些数据背后存在着某种复杂的非线性关系，而且还掺杂着一些随机的噪声干扰。我们的目标是利用 AdaBoost 回归器，把这种隐藏的关系找出来，并通过可视化直观地看到它的预测效果。

1. 生成模拟数据

为了演示 AdaBoost 在回归任务中的表现，我们先创建一组模拟数据。这里用的是常见的正弦函数，再加上一些随机噪声，来模拟现实中复杂多变的数据情况。

import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns
from sklearn.tree import DecisionTreeRegressor
from sklearn.ensemble import AdaBoostRegressor# 生成模拟数据
rng = np.random.default_rng(42)
X = np.sort(5 * rng.random(80))[:, np.newaxis]
y = np.sin(X).ravel() + rng.normal(0, 0.1, X.shape[0])

在这段代码里，我们设定了随机数种子为 42，这样每次运行代码生成的数据都是一样的，方便对比和调试。X是通过生成 80 个 0 到 5 之间的随机数，并整理成一列数据。y则是基于X计算正弦值，再加上一些服从正态分布的随机噪声，模拟出实际观测到的目标值。

2. 构建和训练模型

接下来，我们分别用普通的决策树和 AdaBoost 回归器构建模型，并进行训练。

普通决策树：我们创建一个决策树回归器，限制树的最大深度为 4，避免模型过于复杂导致过拟合。

regr_1 = DecisionTreeRegressor(max_depth=4)

AdaBoost 回归器：AdaBoost 是一种集成学习算法，它的核心思路是把多个 “弱学习器” 组合起来，变成一个强大的模型。这里我们以决策树作为弱学习器，设定总共使用 300 个决策树，并且固定随机种子，保证结果可复现。

regr_2 = AdaBoostRegressor(DecisionTreeRegressor(max_depth=4), n_estimators=300, random_state=42)

然后，我们用生成的X和y数据分别训练这两个模型：

regr_1.fit(X, y)
regr_2.fit(X, y)

训练完成后，使用这两个模型对数据进行预测：

y_1 = regr_1.predict(X)
y_2 = regr_2.predict(X)

3. 可视化对比结果

为了直观地看出两个模型的预测效果差异，我们使用matplotlib和seaborn库绘制图形。

# 可视化结果
colors = sns.color_palette("colorblind")
plt.figure(figsize=(10, 6))
plt.scatter(X, y, color=colors[0], label="training samples")
plt.plot(X, y_1, color=colors[1], label="Decision Tree", linewidth=2)
plt.plot(X, y_2, color=colors[2], label="AdaBoost", linewidth=2)
plt.xlabel("data")
plt.ylabel("target")
plt.title("Decision Tree and AdaBoost Regression")
plt.legend()
plt.show()

在绘制的图形中：

散点表示我们生成的原始数据点，能看到数据分布呈现出一定的非线性趋势，但又因为噪声的存在显得有些杂乱。
蓝色的线是普通决策树的预测结果，它虽然也尝试去拟合数据，但可能因为数据的复杂性和噪声影响，有些地方和真实数据偏差较大。
橙色的线是 AdaBoost 回归器的预测结果，明显可以看出它更好地贴合了数据的整体变化趋势，即使面对噪声点，也能保持相对稳定的预测效果。

通过这个案例，我们完整地展示了 AdaBoost 在回归任务中的应用过程。从生成模拟数据、构建模型，到最后的可视化对比，我们清楚地看到了 AdaBoost 是如何通过组合多个弱学习器，提升模型对复杂非线性数据的拟合能力和对噪声的抵抗能力。

用神经网络分类 2D 数据集：

要用神经网络处理几个经典的二维数据集分类问题。我们会使用三个合成数据集：形状像弯弯月亮的 “月亮形数据集”，由一大一小两个圆圈构成的 “圆形数据集”，还有加入了一些噪声但基本能直线分开的 “线性可分离数据集”。通过调整神经网络里的正则化参数，看看对模型性能有什么影响，最后再把决策边界画出来，直观感受模型是怎么分类的。

1. 数据准备

我们先准备好要用的数据集：

月亮形数据集：用make_moons函数生成，数据点分布成两个相互交叠的半圆形，就像两个弯弯的月亮碰在一起，noise=0.3表示给数据加上一些随机噪声，让分类更有挑战性。
圆形数据集：用make_circles函数生成，包含一大一小两个同心圆的数据点，noise=0.2是噪声，factor=0.5控制两个圆的距离。
线性可分离数据集：用make_classification函数创建，设定只有 2 个有效特征，没有冗余特征，每个类别数据聚成一团，再加入少量噪声，让数据不是完美分开。

# 创建数据集
datasets = [make_moons(noise=0.3, random_state=0),make_circles(noise=0.2, factor=0.5, random_state=1),make_classification(n_features=2, n_redundant=0, n_informative=2, random_state=0, n_clusters_per_class=1)
]

2. 构建神经网络模型

我们搭建一个有两层隐藏层的多层感知机（MLP）分类器。这里重点调整正则化参数alpha，alpha越大，对模型复杂度的限制就越强，能防止模型过拟合。我们选了 5 个不同的alpha值，从 0.1 到 10，覆盖不同的正则化强度。

# 定义不同的alpha值
alphas = np.logspace(-1, 1, 5)# 为每个alpha值构建一个MLP分类器
classifiers = []
names = []
for alpha in alphas:classifiers.append(MLPClassifier(solver="lbfgs",alpha=alpha,random_state=1,max_iter=2000,hidden_layer_sizes=[10, 10]))names.append(f"alpha {alpha:.2f}")

每个模型都用 “lbfgs” 优化器，设定随机种子保证结果可重复，最多训练 2000 次，两层隐藏层都包含 10 个神经元。

3. 数据预处理与模型训练

拿到数据后，先做标准化处理，把数据缩放到统一范围，这样模型训练更快更稳定。再把数据分成 60% 的训练集和 40% 的测试集。

for X, y in datasets:X = StandardScaler().fit_transform(X)X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.4)

4. 可视化决策边界和模型性能

我们创建一个大画布，准备把不同数据集、不同alpha值下的模型表现都画出来。先画出原始数据点，训练集用亮色，测试集颜色淡一点，方便区分。

figure = plt.figure(figsize=(17, 9))
i = 1
for X, y in datasets:# 数据预处理和划分X = StandardScaler().fit_transform(X)X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.4)# 确定绘图范围并生成网格x_min, x_max = X[:, 0].min() - 0.5, X[:, 0].max() + 0.5y_min, y_max = X[:, 1].min() - 0.5, X[:, 1].max() + 0.5xx, yy = np.meshgrid(np.arange(x_min, x_max, h), np.arange(y_min, y_max, h))cm = plt.cm.RdBucm_bright = ListedColormap(["#FF0000", "#0000FF"])ax = plt.subplot(len(datasets), len(classifiers) + 1, i)ax.scatter(X_train[:, 0], X_train[:, 1], c=y_train, cmap=cm_bright)ax.scatter(X_test[:, 0], X_test[:, 1], c=y_test, cmap=cm_bright, alpha=0.6)ax.set_xlim(xx.min(), xx.max())ax.set_ylim(yy.min(), yy.max())ax.set_xticks(())ax.set_yticks(())i += 1

接着，对每个alpha值对应的模型，先在训练集上训练，再用测试集计算准确率。根据模型输出类型，绘制决策边界，颜色深的地方表示模型对分类更确定，颜色浅的地方表示分类不那么明确。最后在图上标注模型的准确率，方便对比。

    for name, clf in zip(names, classifiers):ax = plt.subplot(len(datasets), len(classifiers) + 1, i)clf.fit(X_train, y_train)score = clf.score(X_test, y_test)if hasattr(clf, "decision_function"):Z = clf.decision_function(np.column_stack([xx.ravel(), yy.ravel()]))else:Z = clf.predict_proba(np.column_stack([xx.ravel(), yy.ravel()]))[:, 1]Z = Z.reshape(xx.shape)ax.contourf(xx, yy, Z, cmap=cm, alpha=0.8)ax.scatter(X_train[:, 0], X_train[:, 1], c=y_train, cmap=cm_bright, s=25)ax.scatter(X_test[:, 0], X_test[:, 1], c=y_test, cmap=cm_bright, s=25, alpha=0.6)ax.set_xlim(xx.min(), xx.max())ax.set_ylim(yy.min(), yy.max())ax.set_xticks(())ax.set_yticks(())ax.set_title(name)ax.text(xx.max() - 0.3, yy.min() + 0.3, f"{score:.3f}", size=15, horizontalalignment="right")i += 1

最后调整一下子图布局，让图表看起来更整齐，再展示出来。