计算方法实验三 解线性方程组的直接方法
【实验性质】
综合性实验。
【实验目的】
掌握Gauss消元法和追赶法求解线性方程组。
【实验内容】
应用列主元消去法和追赶法迭代法求解下方程组：
【理论基础】线性方程组的数值解法分直接算法和迭代算法。
直接算法经过有限次的运算后可求得（如果没有舍入误差）方程组的精确解，比如高斯消元法、矩阵分解法、追赶法等。直接法程序复杂，但运算量较小。由于受到计算机字长的限制，直接法也得不到精确解，仅适用于系数矩阵阶数不太高的线性方程组。
1.Gauss算法
Gauss消元法分消元和回代两个过程，消元和回代过程都要求主元非零。如果经过k-1步后的主元 
，则可进行下一步：
Gauss算法的特点是顺序消元，又称顺序高斯消元法，与线性代数的处理方法有显著的不同，请同学们注意。计算过程中，如果出现主元为0，将使Gauss算法的计算终止。
注意：如果系数矩阵为严格对角占优（即
），则高斯消元法一定可以进行到底（即：不会出现主元为0）。
在线性代数中，只要系数行列式
，线性方程组就可求解，遇到主元为零，可以使用行互换操作，把主元上的0换为非0，从而可以继续计算。
本算法中的 Gauss 方法没有行互换选项，当主元为 0 时不能继续进行，因此顺序高斯消元法有缺陷。
另一方面，即使顺序高斯消元法可行，但主元
很小，计算过程中将以它为分母做除法操作，也会
导致其它元素数量级的严重增长和舍入误差的扩散。这是Gauss法的另一缺陷。
主元素消去法是对上述算法的改进，其中列主元消去法较为常用：在第i步，从第i列的第i行至最后一行中选取绝对值最大的元素（注意，不是该列的所有元素，而是部分元素），通过行互换，将其调到主元位置，然后再做消元。
用列选主元方法可以克服高斯消元法的额外限制，只要方程组有解，列选主元方法就能畅通无阻地顺利求解，同时提高了解的精确度。
【提示：用矩阵存放系数矩阵，用向量存放常数项；结果放到向量中】
2、追赶法
在实践中，常遇到m(如
)对角方程组的求解问题。这类方程组的系数矩阵一般为非奇异矩阵，可先分解为特殊矩阵的积，然后基于相关矩阵可得到求解的快速算法。对于三对角方程组，注意分解所得的两个矩阵的特殊性。
【提示：用三个向量存放系数矩阵三条对角线上的数据】
【实验过程】
1.画出选列主元的算法框图。
2.分别用高斯消元法和列主元消去法求解，（自制）表格比较两种算法的结果与精度，分析实验出现的问题，并总结解决办法。
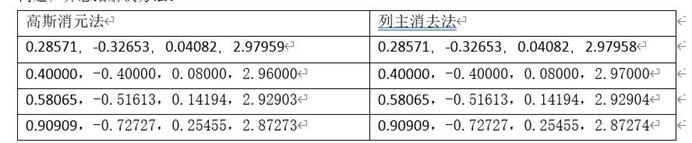
比较结果与精度分析：
高斯消元法的计算过程较为简单直观，但在涉及到除法的操作时会产生小数点的精度问题。在计算过程中，我们可以使用更高精度的浮点数或者避免直接除法运算来解决这个问题。
列主元消去法通过选择主元元素使得计算过程中数值的大小尽量均匀，从而减小了计算误差的累积。因此，列主元消去法的结果一般比高斯消元法更为精确。
两种算法的计算结果在本例中是一致的，但在涉及到更复杂的线性方程组时，可能会出现结果不一致的情况。这是因为两种算法在选择主元和消元顺序上存在差异。为了提高精度，可以应用增加行交换操作来使主元更均匀地分布在矩阵中。
另外，在实际应用中，我们可以利用计算机的计算能力和精度，使用更高精度的数据类型来进行计算，如使用double类型代替float类型。
问题和解决方法：
系数矩阵不可逆： 如果线性方程组的系数矩阵不可逆，即存在行或列线性相关，那么无法求解出唯一解。在这种情况下，高斯消元法和列主元消去法都会出现无法计算的情况。因此，可以通过计算系数矩阵的行列式来判断是否可逆。
数值精度问题： 在计算过程中，可能会出现浮点数计算的精度问题。这可能导致计算结果的误差积累，从而导致最终结果的误差。一种解决办法是使用高精度计算库来进行计算，或者在计算过程中控制舍入误差。
3.用追赶法求解，分别给出两个方程组 Ly = f 和Ux = y ，分析实验出现的问题，并总结解决办法。
问题：
- 方程组可能不满足追赶法的条件：追赶法要求方程组的系数矩阵是三对角矩阵。如果方程组不满足这个条件，追赶法无法直接使用。可以通过对方程组进行预处理，将其转化为满足追赶法条件的形式，然后再进行求解。
- 方程组可能出现数值不稳定性：由于追赶法涉及到前代法和回代法，而这两种方法本身对于某些特殊情况可能出现数值不稳定性的问题。例如，当系数矩阵的某些对角线元素接近零或非常大时，求解过程可能会出现数值溢出或数值误差积累的问题。可以通过增加数值稳定性的措施，如使用行交换或列交换来改善数值稳定性。
- 矩阵分解过程可能需要较大的计算量：追赶法需要对系数矩阵进行分解，这一过程的计算量与方程组的规模有关。对于较大的方程组，矩阵分解可能需要较长的计算时间和内存空间。可以通过使用更高效的分解方法或优化算法来减少计算量。
解决方法：
- 对方程组进行预处理：如果方程组不满足追赶法的条件，可以通过对方程组进行预处理，将其转化为满足条件的形式。预处理的方法可以包括行交换、列交换、行缩放或列缩放等。
- 提高数值稳定性：可以尝试增加数值稳定性的措施，如使用行交换或列交换来改善数值稳定性。此外，也可以尝试使用更稳定的算法或数值方法。
- 优化算法或分解方法：可以考虑使用更高效的算法或分解方法来减少计算量。例如，可以使用更快速和稳定的矩阵分解方法，或使用并行计算等技术来加速求解过程。
4.从使用条件、运算量两个方面比较列主元消去法和追赶法。
使用条件：
- 列主元消去法要求矩阵的列主元不为零。如果矩阵的某个列主元接近于零，则需要进行行交换来保证主元不为零。这增加了算法的复杂性。
- 追赶法没有对矩阵主元的特殊要求，可以直接应用于任意矩阵。
运算量：
- 列主元消去法需要进行列主元的选取和行交换操作，这些操作会增加算法的运算量。
- 追赶法不需要进行主元选取和行交换操作，只需要进行简单的矩阵乘法和加法操作，因此运算量较小。
【实验心得】
在掌握Gauss消元法和追赶法求解线性方程组的过程中，我体会到了它们各自的特点和适用范围。Gauss消元法是一种基础且常用的线性方程组求解方法，它通过消元和回代的过程，将线性方程组化为一个上三角矩阵，进而求解出方程组的解。这种方法适用于各种情况下的线性方程组，但当矩阵的某个主元接近于零时，可能会导致算法的失效或数值不稳定的问题。因此，在应用Gauss消元法时，需要对矩阵的特性进行分析，避免出现这种情况。追赶法是一种特殊的线性方程组求解方法，适用于对带状矩阵（即非零元素集中在主对角线附近的矩阵）进行求解。追赶法通过对矩阵进行LU分解，将原始方程组化为一个三对角矩阵，然后使用追赶法的特殊迭代过程求解出方程组的解。相对于Gauss消元法，追赶法具有更小的运算量和更高的计算效率。
在实际应用中，我发现掌握这两种方法对于求解线性方程组非常有帮助。对于一般情况下的线性方程组，我会优先选择使用Gauss消元法进行求解，因为它是一种通用且可靠的方法。而对于带状矩阵的线性方程组，我则会选择使用追赶法，以提高求解效率。