PINNs案例——多介质分区温度场
基于物理信息的神经网络是一种解决偏微分方程计算问题的全新方法…
有关PINN基础详见:PINNs案例——中心热源温度场预测问题的torch代码
多介质PINN
传统PINNs在多介质问题上由于不同介质参数不同,对应PDE方程参数不同,求解困难。
本文采用多个神经网络分区求解方法,给出了多介质传热问题的求解案例。
该案例参考学习论文:
陈豪龙, 唐欣越, 王润华, 周焕林, 柳占立. 基于物理信息神经网络的多介质非线性瞬态热传导问题研究. 力学学报, 2024, 56(12): 1-14. DOI: 10.6052/0459-1879-24-337

问题场景
- 求解域:案例选取边长为 1 的正方形区域作为研究对象,定义域为
Ω = [ 0 , 1 ] × [ 0 , 1 ] \Omega = [0,1] \times [0,1] Ω=[0,1]×[0,1]。区域内水平方向等距离分为三种介质

- 参数设定 从左至右三种介质热导率分别设置为 λ 1 = 0.1 , λ 2 = 0.3 , λ 3 = 0.5 \lambda_1 = 0.1 ,\lambda_2 = 0.3,\lambda_3 = 0.5 λ1=0.1,λ2=0.3,λ3=0.5。
- 边界条件:区域左边界温度为10,右边界温度为30
- 求解量:区域内二维稳态温度场分布
PINNs理论求解
在该正方形区域内,温度场 $ T(x, y) $ 满足二维稳态导热方程,数学表达为:
− κ ( ∂ 2 T ∂ x 2 + ∂ 2 T ∂ y 2 ) = q -\kappa \left( \frac{\partial^2 T}{\partial x^2} + \frac{\partial^2 T}{\partial y^2} \right) = q −κ(∂x2∂2T+∂y2∂2T)=q
其中:
- κ \kappa κ 为材料的热导率(thermal conductivity),表示材料传导热量的能力;
- q q q 为内热源(heat source),表示单位体积内热量的产生率;
- T ( x , y ) T(x, y) T(x,y) 为温度分布函数。
相比 PINNs案例——中心热源温度场预测问题的torch代码,本次案例中,求解区域PDE方程中的$ \kappa $ 值不同,可以通过神经网络分区进行求解,设计多个神经网络控制不同区域,再添加每个介质边界条件的损失函数,以确保整个求解域的连续性。对所有损失函数进行累加后,反向传播,使用一个优化器优化每个神经网络的所有参数。
损失函数可以表示为:
- **PDE 残差项:**区域不含热源,且不同区域热导率不同, κ \kappa κ 为关于 x y xy xy 的函数.故控制方程如下:
Loss PDE = 1 N c ∑ i = 1 N c ∣ f ( x c i , y c i ) ∣ 2 \text{Loss}_{\text{PDE}} = \frac{1}{N_c} \sum_{i=1}^{N_c} \left| f\left( x_c^i, y_c^i \right) \right|^2 LossPDE=Nc1i=1∑Nc f(xci,yci) 2
f ( x c i , y c i ) = κ ( x , y ) ( ∂ 2 T ∂ x 2 + ∂ 2 T ∂ y 2 ) f\left( x_c^i, y_c^i \right) = \kappa (x,y) \left( \frac{\partial^2 T}{\partial x^2} + \frac{\partial^2 T}{\partial y^2} \right) f(xci,yci)=κ(x,y)(∂x2∂2T+∂y2∂2T) - 边界条件项:在多介质问题中,边界条件除热边界固定温度,绝热边界等,还要添加不同介质交界面的连续性边界条件
-
固定温度边界:
Loss BC = 1 N b ∑ i = 1 N b ∣ T ( x b i , y b i ) − T f i x e d ∣ 2 \text{Loss}_{\text{BC}} = \frac{1}{N_b} \sum_{i=1}^{N_b} \left| T\left( x_b^i, y_b^i \right) - T_{fixed} \right|^2 LossBC=Nb1i=1∑Nb T(xbi,ybi)−Tfixed 2 -
介质交界面:
不同热导率介质的边界条件包含第一类边界条件和第二类边界条件:
第一类边界条件(不同介质在边界面上温度连续):
Loss I1 = 1 N I ∑ j = 1 N I ∣ λ p T p ( x I j ) − λ p + 1 T p + 1 ( x I j ) ∣ 2 \text{Loss}_{\text{I1}} = \frac{1}{N_{I}}\sum_{j=1}^{N_{I}}\left|\lambda_{p}\ T_{p}\left(x_{I}^{j}\right)-\lambda_{p+1} T_{p+1}\left(x_{I}^{j}\right)\right|^{2} LossI1=NI1j=1∑NI λp Tp(xIj)−λp+1Tp+1(xIj) 2
第一类边界条件(不同介质在边界面上温度法向导数与热导率的乘积连续):
Loss I2 = 1 N I ∑ j = 1 N I ∣ λ p ∂ T p ( x I j ) ∂ n − λ p + 1 ∂ T p + 1 ( x I j ) ∂ n ∣ 2 \text{Loss}_{\text{I2}} = \frac{1}{N_{I}}\sum_{j=1}^{N_{I}}\left|\lambda_{p}\frac{\partial T_{p}\left(x_{I}^{j}\right)}{\partial n}-\lambda_{p+1}\frac{\partial T_{p+1}\left(x_{I}^{j}\right)}{\partial n}\right|^{2} LossI2=NI1j=1∑NI λp∂n∂Tp(xIj)−λp+1∂n∂Tp+1(xIj) 2
其中:
- N I N_I NI 表示介质边界点的点数
- T p T_p Tp 表示第P个介质
- λ p \lambda_ {p} λp 表示第P个介质的热导率
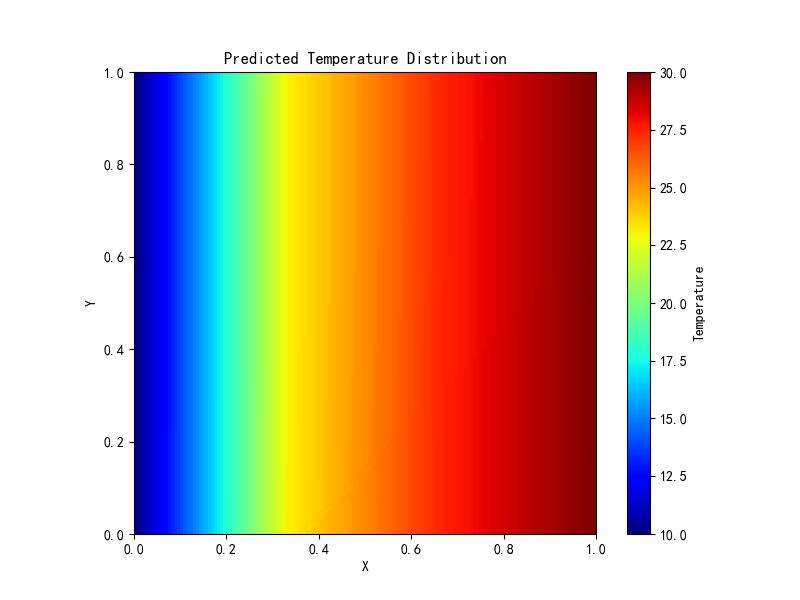
复现结果


采用6000次adam优化与lbfgs优化器进行优化。各项损失收敛过程如下,收敛效果良好:

代码请关注:
