动态规划简单题

以leetcode746（使用最小花费楼梯）进一步巩固动态规划答题步骤

解析题目：

读题+题目要求，要求计算并且返回到达楼顶的最低花费，你可以从0或者1号台阶开始，每一次能走1个或者2个台阶，注意观察测试用例，到达的楼顶为数组的最后一个的下一个，也就是要花15元到数组外面，如果楼顶位置位20那个位置，就可以花10到达，显然楼顶位置在20的那个位置的下一个位置（把所有台阶都跨过去之后的那个位置才是楼顶）

算法原理 ：

状态表示：经验+题目要求（一般一维数组，这里的经验就是以i位置为结尾，然后巴拉巴拉）

这里的巴拉巴拉要根据题目要求进行补充。

例如，以i位置为结尾说明我已经到达了第i个位置，根据题目要求，可以分析dp[i]为到达i位置的最小花费，也就是每个dp都是到达某个位置的最小花费，dp[0]就是到达第0个位置的最小花费

所以综上状态表示就是dp[i]:表示到达i位置时的最小花费

状态转移方程：就是求dp[i]=什么

也就是用之前或者之后的状态推导出dp[i]的值，之前的状态就是dp[i-1]/dp[i-2]，之后的状态就是dp[i+1]/dp[i+2]等

分析：根据最近的一步划分子问题

到达i位置之前是不是需要先到达i-1位置，花费cost[i-1]然后到达i位置

或者先到达i-2的位置，花费cost[i-2]然后到达i的位置

所以，cost[i-1]是固定的，怎么求到达i-1的最小花费，是不是有点熟悉，我们的状态表示dp[i-1]就是表示到达i-1的最小花费

所以我们只要比较dp[i]=min(dp[i-1]+cost[i-1],dp[i-2]+cost[i-2]),这样就可以求得dp[i]的值

初始化：保证填表的时候不越界

题目要求你是从0/1号位置开始的，也就是你到达0/1时是没有花费的，dp[0]=dp[1]=0,也就是你要初始化0/1，否则你在dp[i]=min(dp[i-1]+cost[i-1],dp[i-2]+cost[i-2]),中的i-2就会越界

填表顺序：

从左往右

返回值：

返回dp[n] 

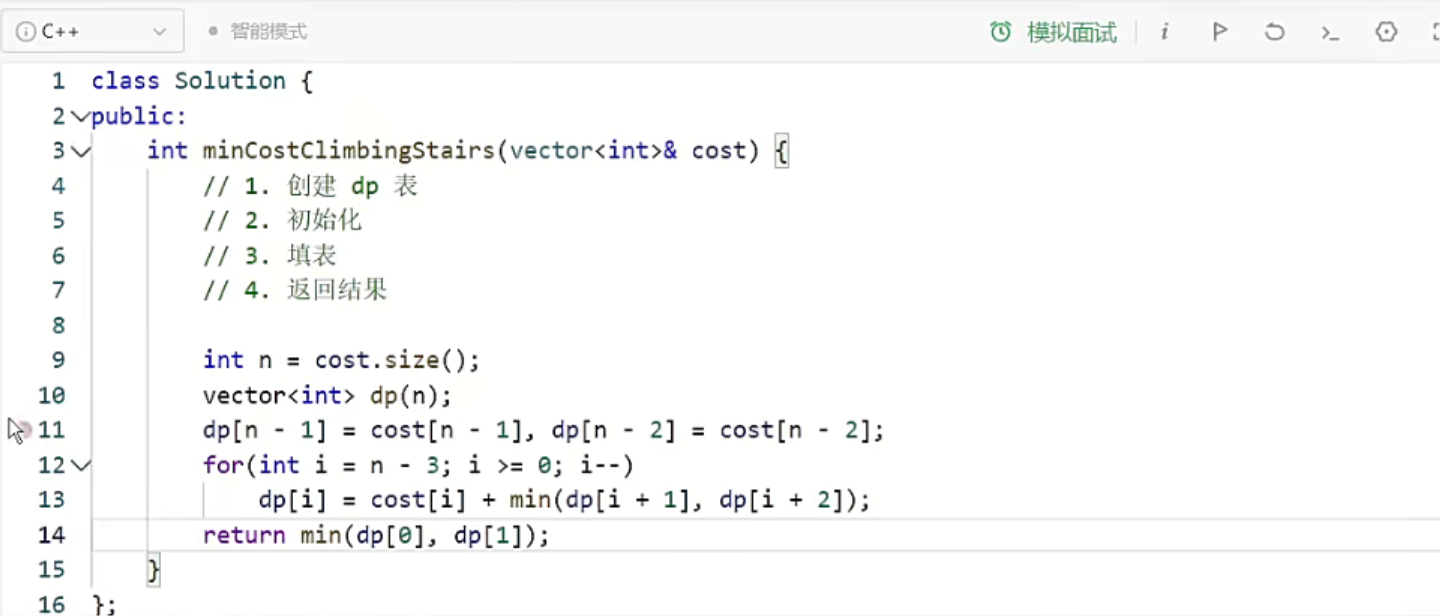
编写代码

默认初始化已经为0，创建dp对象的时候 

第二种解法

也是一种动态规划的思想，只是状态表示方法不同

第一种状态表示是以i位置为结尾，然后巴拉巴拉

第二种解法状态表示是以i位置为起点，然后巴拉巴拉

分析可得状态表示：以i位置出发，到达楼顶的最小花费

状态转移方程

这个是第一种解法的状态转移方程分析图

那第二种该如何想呢？你的状态dp[i]:为以i位置出发，到达楼顶的最小花费

dp[i]支付cost[i]的钱，走一步到达i+1，从dp[i+1]到达终点的最小花费是不是dp[i+1]+cost[i]

dp[i]支付cost[i]的钱，走两步到达i+2,从dp[i+2]到达终点的最小花费是不是dp[i+2]+cost[i]