机器学习——朴素贝叶斯法运用
一、朴素贝叶斯法
1.1 基本概念
朴素贝叶斯法是一种基于贝叶斯定理的简单概率分类方法,它假设特征之间相互独立。它适用于分类问题,尤其是在文本分类中表现良好。其核心思想是通过考虑各个特征的概率来预测分类(即对于给出的待分类样本,计算该样本在每个类别下出现的概率,最大的就被认为是该分类样本所属于的类别
1.2 朴素贝叶斯的一般过程
1.准备数据:收集并预处理数据,将数据分为特征和标签
2.特征选择:选择对分类有帮助的特征
3.模型训练:使用训练数据计算每个类别的先验概率和条件概率
4.预测:对新数据进行分类,选择概率最大的类别作为预测结果
1.3 朴素贝叶斯的优缺点
1.优点
- 具有稳定的分类效率
- 在数据较少时仍然有效,可以处理多类别的问题
- 对缺失数据不太敏感
- 进行分类时对时间和空间的开销都比较小
2.缺点
- 对于输入数据的准备方式比较敏感,需要对数据进行适当的预处理
- 需要假设属性之间相互独立,这在实际情况中往往不太现实
- 需要知道先验概率,但是由于先验概率大多取决于假设,故很容易因此导致预测效果不佳
1.4 朴素贝叶斯应用场合
朴素贝叶斯主要被广泛地应用在文本分类、垃圾邮件过滤、情感分析等场合
二、算法原理
2.1 计算公式
1.贝叶斯定理
朴素贝叶斯算法的核心是贝叶斯定理,公式如下:

其中:
- P(y|X)是后验概率,即在给定特征 X 的情况下类别 y 的概率
- P(X|y)是条件概率,即在类别 y 的情况下特征 X 的概率
- P(y)是类别y的先验概率
- P(X)是特征X的边缘概率
2.条件独立性假设
联合概率分解为:

3.最终分类决策
选择使后验概率最大的类别:

2.2 计算步骤
1.计算先验概率

2.计算条件概率
离散特征:
连续特征(假设服从高斯分布):
3.计算联合后验概率(取对数避免下溢)

4.计算最大概率对应的类别

2.3 贝叶斯公式涉及概率
- 先验概率:根据以往的经验和分析得出的,对某个事件发生概率的初始假设估计
- 条件概率:指在某个事件A已经发生的条件下,另一个事件B发生的概率
- 后验概率:指在考虑了新的证据或数据之后,我们对某个事件发生的概率的更新估计
- 边缘概率:指不考虑其他事件的情况下,某个事件发生的概率
- 联合概率:指两个或多个事件同时发生的概率
2.4 平滑处理(避免零概率事件)
1.拉普拉斯平滑(适用于离散特征):

三、实例:判断西瓜好坏
3.1 测试数据
1.相关数据集
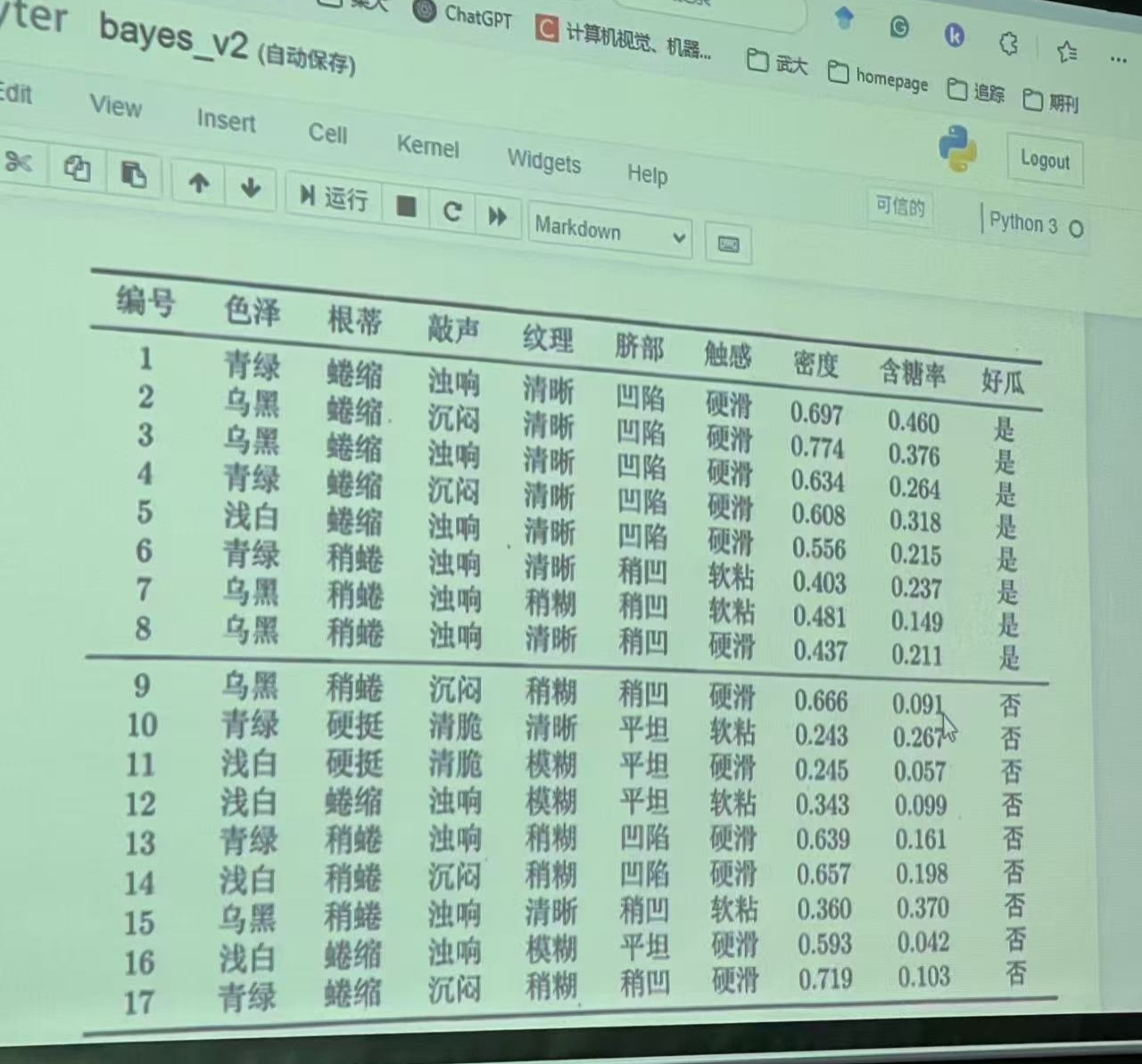
2.对新数据进行西瓜品质分类,测试数据如下
| 编号 | 色泽 | 根蒂 | 敲声 | 纹理 | 脐部 | 触感 | 密度 | 含糖率 | 好瓜 |
| 测1 | 青绿 | 蜷缩 | 浊响 | 清晰 | 凹陷 | 硬滑 | 0.697 | 0.460 | ? |
3.2 数据集分析
1.计算先验概率
在所给的相关数据集中,总共有17个数据,其中最后判别结果为好瓜的有8个,坏瓜的有9个,分别计算好瓜和坏瓜的先验概率,如下图:

2.计算条件概率
(1)离散特征(色泽、根蒂等):

(2)连续特征(密度、含糖率等)(假设服从高斯分布):
由于 密度=0.697 和 含糖率=0.460 在坏瓜中没有出现(概率=0),直接计算会导致零概率问题,因此需要使用拉普拉斯平滑调整:
调整后的概率:
3.计算联合后验概率(直接相乘)
(1)好瓜的联合后验概率:

(2)坏瓜的联合后验概率:

4.比较后验概率
由好瓜和坏瓜的联合后验概率计算结果可以很明显的看出:
P( 好瓜 | x) > P( 坏瓜 | x)
因此我们可以得出结论,预测测1的西瓜为好瓜
3.3 测试代码
import numpy as np
import pandas as pd# 加载数据集函数
def loadDataset():dataset = [['青绿', '蜷缩', '浊响', '清晰', '凹陷', '硬滑', 0.697, 0.460, '是'],['乌黑', '蜷缩', '沉闷', '清晰', '凹陷', '硬滑', 0.774, 0.376, '是'],['乌黑', '蜷缩', '浊响', '清晰', '凹陷', '硬滑', 0.634, 0.264, '是'],['青绿', '蜷缩', '沉闷', '清晰', '凹陷', '硬滑', 0.608, 0.318, '是'],['浅白', '蜷缩', '浊响', '清晰', '凹陷', '硬滑', 0.556, 0.215, '是'],['青绿', '稍蜷', '浊响', '清晰', '稍凹', '软粘', 0.403, 0.237, '是'],['乌黑', '稍蜷', '浊响', '稍糊', '稍凹', '软粘', 0.481, 0.149, '是'],['乌黑', '稍蜷', '浊响', '清晰', '稍凹', '硬滑', 0.437, 0.211, '是'],['乌黑', '稍蜷', '沉闷', '稍糊', '稍凹', '硬滑', 0.666, 0.091, '否'],['青绿', '硬挺', '清脆', '清晰', '平坦', '软粘', 0.243, 0.267, '否'],['浅白', '硬挺', '清脆', '模糊', '平坦', '硬滑', 0.245, 0.057, '否'],['浅白', '蜷缩', '浊响', '模糊', '平坦', '软粘', 0.343, 0.099, '否'],['青绿', '稍蜷', '浊响', '稍糊', '凹陷', '硬滑', 0.639, 0.161, '否'],['浅白', '稍蜷', '沉闷', '模糊', '凹陷', '硬滑', 0.657, 0.198, '否'],['乌黑', '稍蜷', '浊响', '清晰', '稍凹', '软粘', 0.360, 0.370, '否'],['浅白', '蜷缩', '浊响', '模糊', '平坦', '硬滑', 0.593, 0.042, '否'],['青绿', '蜷缩', '沉闷', '稍糊', '稍凹', '硬滑', 0.719, 0.103, '否']]testset = [['青绿', '蜷缩', '浊响', '清晰', '凹陷', '硬滑', 0.697, 0.460]]labels = ['色泽', '根蒂', '敲声', '纹理', '脐部', '触感', '密度', '含糖率', '好瓜']return dataset, testset, labels# 计算先验概率P(C)
def prior(C):dataset = loadDataset()[0]counts = 0countAll = len(dataset)for item in dataset:if item[-1] == C:counts += 1P_C = round(counts / countAll, 3)return P_C# 计算条件概率P(x|C)
def P_x_given_C(x, C, labels=loadDataset()[2]):dataset = loadDataset()[0]counts = 0countB = 0for item in dataset:if item[-1] == C:lst = [item[index] for index, feature in enumerate(labels) if feature != '好瓜']if x in lst:counts += 1countB += 1P_x_given_C = round(counts / countB, 3)return P_x_given_C# 计算所有特征的后验概率并进行比较
def classify():dataset, testset, labels = loadDataset()test_data = testset[0]results = []for cla in ('是', '否'):p = prior(cla)for x in test_data:fx_x_given_c = P_x_given_C(x, cla, labels)p *= fx_x_given_cresults.append((cla, p))results.sort(key=lambda x: x[1], reverse=True)return results[0][0]# 预测新数据
new_data = ['青绿', '蜷缩', '浊响', '清晰', '凹陷', '硬滑', 0.697, 0.460
]
prediction = classify()
print("新数据特征:", new_data)
print("预测结果:", "好瓜" if prediction == '是' else "坏瓜")3.4 测试结果分析
1.运行截图

2.结果分析
- 加载数据集函数(loadDataset)
(1)这个函数定义了训练数据集和测试数据集,以及它们的标签
(2)数据集包括特征如色泽、根蒂、敲声等,以及目标变量“好瓜”
- 计算先验概率(prior)
(1)这个函数计算给定类别(“是”或“否”)的先验概率
(2)它通过计算每个类别在数据集中出现的次数与总数据集大小的比例来实现
- 计算条件概率
(1)这个函数计算在给定类别下某个特征值的条件概率
(2)它通过计算该特征值在特定类别下出现的次数与该类别总出现次数的比例来实现
- 分类函数(classify)
(1)这个函数使用朴素贝叶斯定理来预测测试数据的类别。
(2)它计算测试数据在每个类别下的后验概率,并选择概率最大的类别作为预测结果
- 预测结果分析
测试数据:
- 色泽: 青绿
- 根蒂: 蜷缩
- 敲声: 浊响
- 纹理: 清晰
- 脐部: 凹陷
- 触感: 硬滑
- 密度: 0.697
- 含糖率: 0.460
预测结果:
- 根据代码输出,预测结果为“好瓜”
- 结果合理性
- 数据分布:在训练数据中,具有相似特征的西瓜大多数被标记为“好瓜”。这表明模型有足够的证据将这些特征与“好瓜”类别关联起来
- 模型假设:朴素贝叶斯模型假设特征之间相互独立,这在实际应用中可能不完全成立,但通常可以提供合理的预测结果,尤其是在特征数量较多且特征之间确实相对独立的情况下
- 模型性能:由于朴素贝叶斯模型简单且计算效率高,它通常适用于初步的分类任务。然而,对于更复杂的数据集或需要更高精度的应用,可能需要考虑更复杂的模型




