【漫话机器学习系列】225.张量(Tensors)
深度学习中的张量(Tensor)到底是什么?一文彻底讲清楚!
在机器学习和深度学习领域,无论是使用 TensorFlow、PyTorch 还是其他框架,我们都会频繁遇到一个术语:张量(Tensor)。
但很多初学者对张量的理解只停留在“好像是数组?”的阶段。实际上,张量既简单又强大,它是支撑现代深度学习系统的基础。
本文通过直观图示,带你彻底掌握张量的概念、分类和在实际应用中的意义。
一、什么是张量(Tensor)?
简单来说,张量就是一种多维数组。
它们以网格(Grid)状坐标形式排列数值,可用来表示数据的不同形态,比如一个向量、一张图片,甚至是一个视频序列。
正如图中所示:
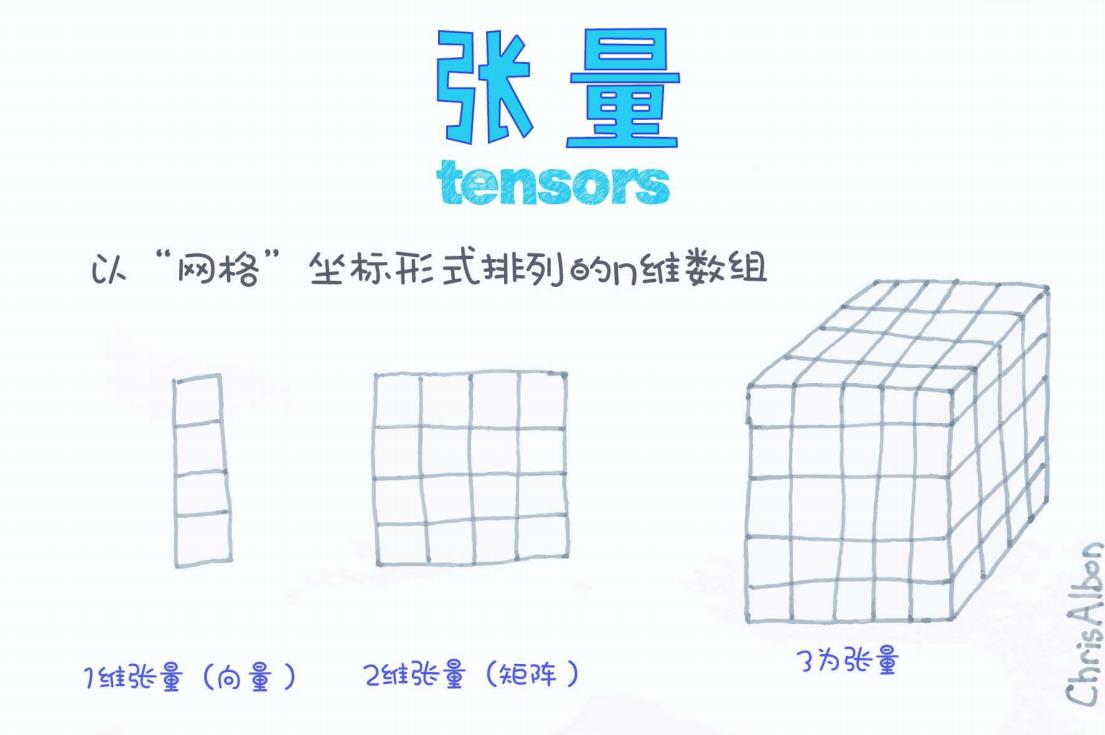
| 维度 | 形态 | 示例 |
|---|---|---|
| 1维张量 | 向量(Vector) | |
| 2维张量 | 矩阵(Matrix) | |
| 3维张量 | 数据立方体(Data Cube) | 多张图片叠加或彩色图像(RGB通道) |
二、张量各维度的直观理解
让我们逐一来看:
1. 一维张量(向量)
-
结构:一串线性排列的数字
-
形象理解:一列数字,就像一条直线
-
示例应用:表示特征列表(如一个人的身高、体重、年龄等)
图中左边部分就是一维张量示意图:
形状(Shape):,只有一个维度。
2. 二维张量(矩阵)
-
结构:数字排列成行和列的表格
-
形象理解:就像一张二维表格或 Excel 工作表
-
示例应用:图片的灰度像素、词嵌入矩阵(Embedding Matrix)
图中中间部分展示的是二维张量:
形状(Shape):,有行有列。
3. 三维张量
-
结构:多个矩阵叠加在一起,形成立体结构
-
形象理解:一个“数据立方体”
-
示例应用:
-
彩色图像(RGB三个通道)
-
多帧组成的视频片段(时间、宽度、高度)
-
Batch处理(多张图像作为一个批次)
-
图中右边部分就是三维张量的直观展示:
形状(Shape):,包含多个二维矩阵。
三、张量为什么重要?
在深度学习中,所有数据都是以张量的形式表示和计算的,包括输入数据、模型参数、输出结果等。
不论你是进行图像识别、自然语言处理,还是做强化学习,张量都是基本的计算单位。
比如:
-
输入一张彩色图片 → 是一个三维张量(宽 × 高 × 通道数)
-
隐藏层权重矩阵 → 是一个二维张量(输入特征数 × 输出特征数)
-
批量训练数据 → 是一个四维张量(批大小 × 通道数 × 高度 × 宽度)
张量不仅支持简单的数据存储,还能进行高效的数学运算(如矩阵乘法、卷积等),这也是深度学习框架优化计算性能的关键。
四、补充:张量与数组(Array)的关系
很多同学会问:张量和普通的数组有什么区别?
可以这样理解:
| 特点 | 数组(Array) | 张量(Tensor) |
|---|---|---|
| 数学背景 | 计算机科学中使用 | 数学/物理中更正式 |
| 运算特性 | 支持加减乘除 | 支持高阶线性代数运算(例如广播机制、梯度计算) |
| 深度学习框架支持 | 部分支持 | 全面支持,且针对硬件加速(GPU/TPU) |
所以,从使用上讲,可以粗略地把张量看作是“功能更强大的数组”。
五、总结
张量是深度学习中用于表示数据的基础结构,具有任意维度,可以看作是“网格状排列的数值组”。
掌握张量的本质是理解神经网络、优化模型结构、提升训练效率的第一步。
本文小结:
-
张量 = 多维数组
-
一维张量 = 向量,二维张量 = 矩阵,三维及以上 = 数据立方体
-
在深度学习中,无论是输入、输出还是中间计算,统统是以张量的形式进行的
如果本文对你理解张量有所帮助,记得点赞支持!也可以在评论区留言你想了解的其他深度学习基础概念,比如 广播机制(Broadcasting)、自动微分(Autograd) 等,后续我会继续更新系列内容!
