《数据结构之美--栈和队列》

一：引言：

上次我们学习了双向链表的实现，这次我们来学习两个新的数据结构，因为比较简单，就放在一块学习。

二：栈的实现

1. 栈的结构与性质

只凭文字来描述的话不够生动，下面我们就以图画的形式来直观感受一下栈。

2. 思考：

既然我们已经知道了栈的结构和性质，那么就是来实现栈。我们用什么来实现栈呢？
先来考虑拿刚学的链表来实现栈：

接着再来考虑用顺序表来实现栈：

可以看到用顺序表和链表实现栈的时间复杂度都为o(1)，那么只好再从空间角度来比较，若用链表来实现的话，需要不停地申请新节点，并且链表的存储结构还不一定连续，容易造成空间的碎片化，而顺序表的话存储结构是一个接一个的连续着的，空间利用率会更好，并且顺序表采用动态数组，也能做到动态扩容，因此，结合以上几点分析，还是用顺序表来实现栈更好一点。

3. 定义栈

因为进栈和出栈都是在栈顶进行，因此这里需要定义栈顶位置，除了动态数组，还需要知道栈的空间大小，因此再定义一个容器大小。

4. 初始化

声明：

注意这里因为要改变结构体中的成员，因此传入的是结构体指针（结构体的地址）

逻辑实现：

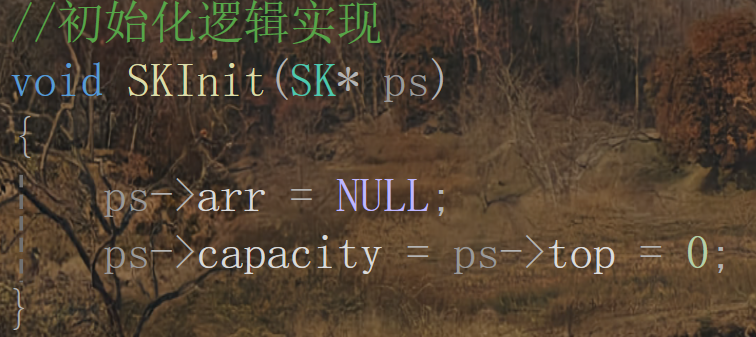
测试：

5. 入栈

声明：

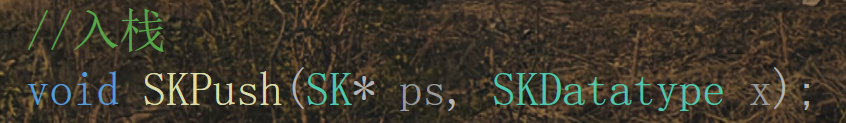
逻辑分析：

逻辑实现：

测试：

可以看到测试正常

6. 出栈

声明：

逻辑分析：

栈的出栈其实就是顺序表的删除逻辑，只需让top--即可，这时top位置的元素就是无效元素了。
注：但进行出栈操作之前还要判断栈是否为空，也就是top是否为0。

逻辑实现：

测试：

可以看到测试没问题

7. 取出栈顶元素

声明：

逻辑实现：

因为在每次入栈之后top会往后走一格，因此栈顶位置即为top - 1

8. 栈中有效元素个数

声明：

逻辑实现：

由于我们是从下标为0的位置开始使用，因此top的值即为栈中有效元素的个数

9.销毁

声明：

逻辑实现：

测试：

三：队列的实现

1. 队列的结构和性质

队列：一种具有先进先出性质的连续存储的数据结构。
下面通过图画来辅助理解：

2.思考：

在知道了队列的性质和结构之后，就是来实现队列，下面我们还是从顺序表和链表的角度来考虑。
先来看顺序表：

接下来再看链表：

通过上述分析可以看到无论是顺序表还是链表，时间复杂度都不能做到入队和出队的时间复杂度同时为o(1)
因此就需要想办法来优化一下：我们可以发现：队列的出队和入队，一个是针对队头，一个是针对队尾，队列的中间部分我们不关心，并且队列是由一个个节点组成的，因此可以分为两个结构，定义一个队列结构，定义一个节点结构，这样就可以实现队列的出队和入队时间复杂度都为o(1)

3. 定义队列

这里我们先定义了每个节点的结构，然后定义了队列结构，其中维护了指向队头和指向队尾的两个结构体指针。

4. 初始化

声明：

这里还是老样子，由于需要修改结构体的成员，要改变实参，因此传入的是结构体指针（结构体的地址）

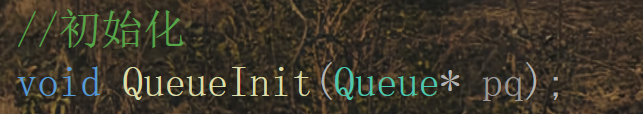
逻辑实现：

测试：

可以看到初始化正常、

5.入队

声明：

逻辑分析：

逻辑实现：

进队分为了两种情况：空队列与非空队列

6. 判空

声明：

逻辑实现：

7.出队

声明：

逻辑分析：

逻辑实现：

8. 取出队头元素

声明：

逻辑实现：

测试：

这里我们让1 2 依次入队，之后我们又执行了一次出队，因此队头就成了2

9. 取出队尾元素

声明：

逻辑实现：

测试：

10.队列中有效元素个数

声明：

逻辑实现：

测试：

11.销毁

声明：

逻辑实现：

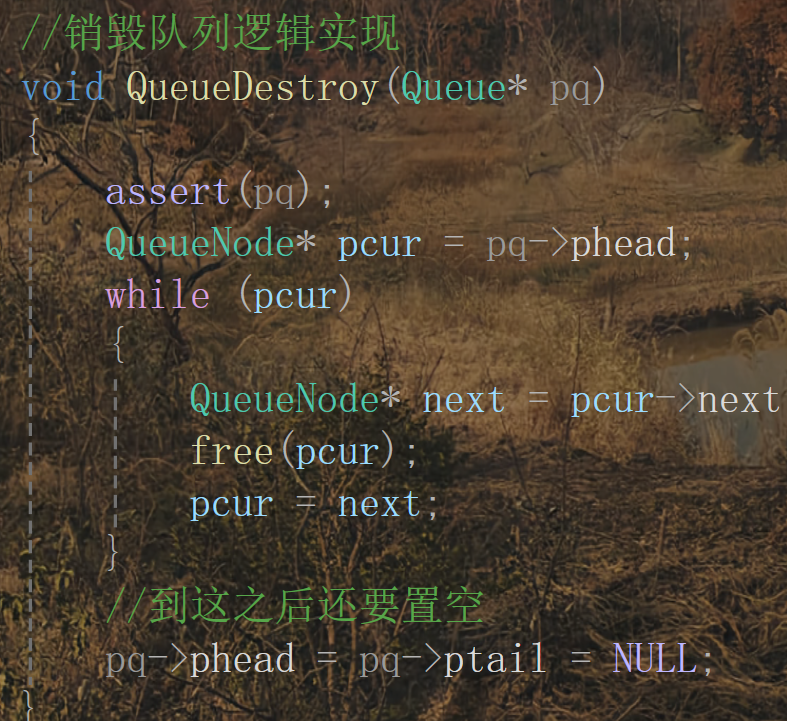
测试：

总结：

在这篇博客中，我们实现了具有先进后出性质的栈和具有先进先出性质的队列。
下篇博客我们将练习几道关于栈和队列的oj题。