【电机仿真】MPC模型预测转速、电流双闭环控制器——PMSM有感FOC控制

【电机仿真】MPC控制器——PMSM有感FOC控制

---

前言

---

提示：以下是本篇文章正文内容，下面案例可供参考

一、clark变换——三相整定为两相

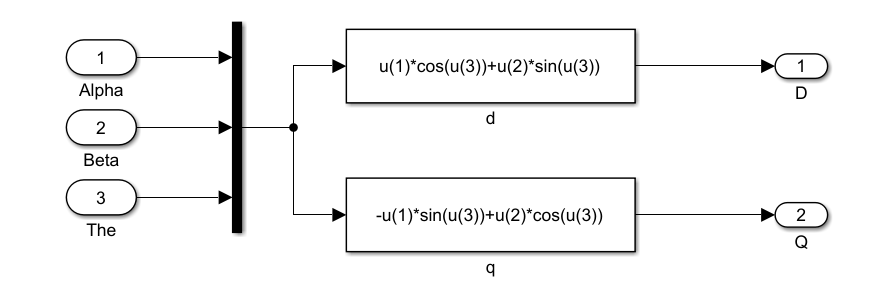
二、park变换——非线性整定为线性

三、控制器——MPC模型预测控制器

MPC 是种基于控制对象数学模型的控制策略，根据所建立的预测模型和输入的给定量来对未来一段时间域的系统的状态值进行预测

1.模型预测速度控制理论

a.预测模型

由机械运动学可建立方程


对SPMSM进行分析，其电磁转矩

代入到上式可得

其K+1时刻实际转速公式为


MATLAB代码为

A=1-F*Ts/J;%定义A B
B=1.5*np*ff*Ts/J;

则K时刻，实际转速公式为

MATLAB代码为

wmk1=A*wk+B*iqk-TL*Ts/J;%计算k+1时刻的实际转速

用k+1时刻减去k时刻，两式相减可得增量模型，即预测转速公式

MATLAB代码为

Wwp=Wwm+Wiq.*dtiq0;%计算转速预测值

b.反馈校正

误差=预测转速-实际转速

MATLAB代码为

e=wmk1-Wwp(1,1);%计算预测转速和实际转速间的误差
for i = 1:NWr(i,1) = wr+delta*e;%反馈校正，调整参考转速
end

c.参考轨迹

为了使 PMSM 实际状态能平滑过渡到目标速度，速度参考轨迹可以选择一阶指数形式，但是本次设计没有使用

d.优化准则——滚轮优化求解

优化准则选取二次型性能指标函数

iq变为求delt

当J有最小值时，MPC控制性能最好，求导移项可得

MATLAB代码为

dtiq=inv(R^(2)+Wiq'*Q*Wiq)*(Wiq'*Q*(Wr-Wwm));%滚动优化求解最小dtiq

因此，速度环输出为

MATLAB代码为

iq = dtiq(1,1)+iqk1;%给出第一个控制量

根据工程经验进行约束

2.模型预测电流控制理论

同转速环

a.预测模型

对SPMSM分析

离散化k+1时刻，实际电流模型为

那么k时刻，实际电流模型为

MATLAB代码为

C=1-Rs*Ts/Lq;%定义C D
D=Ts/Ld;
iqk1=C*iqk+D*uqk;%计算k+1时刻的实际iq

两式相减可得增量模型，即预测电流模型

由工程经验可得，若MCU电流环采样频率太高，电流环采样周期减小，可推出在电流采样一个周期内，速度几乎不变，w(k)-w(k-1)可约为0，则预测电流模型为

MATLAB代码为

    Wiqm(i, 1) = Ci*iqk-Cj*iqkm1;Wuq(i, 1) = Cn*D;
dtuq0=uqk-uqk1;%计算当前电流增量
Wiqp=Wiqm+Wuq.*dtuq0;%计算iq预测值

b.反馈校正

优化准则选取二次型性能指标函数
MATLAB代码为

e=iqk1-Wiqp(1,1);%计算预测iq和实际iq间的误差
for i = 1:NIqr(i,1) = iqr+delta*e;%反馈校正，调整参考转速
end

c.参考轨迹

没有使用

d.优化准则——滚轮优化求解

MATLAB代码为

R=0.001*eye(Nu);
Q=eye(N);
dtuq=inv(R^(2)+Wuq'*Q*Wuq)*(Wuq'*Q*(Iqr-Wiqm));%滚动优化求解最小dtuq
uq = dtuq(1,1)+uqk1;%给出第一个控制量

3.仿真

a.速度环控制器

b.代码

function iq = fcn(iqk,iqk1,wk,wk1,wr,TL)
%定义相关参数
ff=0.3163;
Ts=1e-5;
np=4;
F=0.009;
J=0.014;
delta=80;
N=4;%预测时域
Nu=2;%控制时域A=1-F*Ts/J;%定义A B
B=1.5*np*ff*Ts/J;Wwm = zeros(N,1);%初始化数组
Wiq = zeros(N,1);
Wwp = zeros(N,1);
Wr  = zeros(N,1);
N=4;for i = 1:NAi=0;Aj=0;An=0;for j = 0:NAi = Ai+A^(j);Aj=Ai-1;endfor j = 0:N-1An = An+(N-j)*A^(j);endWwm(i, 1) = Ai*wk-Aj*wk1;Wiq(i, 1) = An*B;
enddtiq0=iqk-iqk1;%计算当前电流增量Wwp=Wwm+Wiq.*dtiq0;%计算转速预测值
wmk1=A*wk+B*iqk-TL*Ts/J;%计算k+1时刻的实际转速
e=wmk1-Wwp(1,1);%计算预测转速和实际转速间的误差for i = 1:NWr(i,1) = wr+delta*e;%反馈校正，调整参考转速
endR=eye(Nu);
Q=eye(N);%权重矩阵设置为单位矩阵
dtiq=inv(R^(2)+Wiq'*Q*Wiq)*(Wiq'*Q*(Wr-Wwm));%滚动优化求解最小dtiq
iq = dtiq(1,1)+iqk1;%给出第一个控制量

c.电流环控制器

d.代码

function uq = fcn(uqk,uqk1,iqk,iqkm1,iqr)
%定义相关参数
ff=0.3163;
Rs=0.994;
np=4;
Ts=1e-6;
Ld=6.3e-3;
Lq=9e-3;
delta=0;
N=4;%预测时域
Nu=2;%控制时域C=1-Rs*Ts/Lq;%定义C D
D=Ts/Ld;Wiqm = zeros(N,1);%初始化数组
Wuq = zeros(N,1);
Wiqp = zeros(N,1);
Iqr  = zeros(N,1);for i = 1:NCi=0;Cj=0;Cn=0;for j = 0:NCi = Ci+C^(j);Cj=Ci-1;endfor j = 0:N-1Cn = Cn+(N-j)*C^(j);endWiqm(i, 1) = Ci*iqk-Cj*iqkm1;Wuq(i, 1) = Cn*D;
enddtuq0=uqk-uqk1;%计算当前电流增量Wiqp=Wiqm+Wuq.*dtuq0;%计算iq预测值
iqk1=C*iqk+D*uqk;%计算k+1时刻的实际iq
e=iqk1-Wiqp(1,1);%计算预测iq和实际iq间的误差for i = 1:NIqr(i,1) = iqr+delta*e;%反馈校正，调整参考转速
endR=0.001*eye(Nu);
Q=eye(N);
dtuq=inv(R^(2)+Wuq'*Q*Wuq)*(Wuq'*Q*(Iqr-Wiqm));%滚动优化求解最小dtuq
uq = dtuq(1,1)+uqk1;%给出第一个控制量

e.实验结果

转速输出曲线

电流输出曲线

四、park反变换

五、SVPWM

六、三相逆变电路

七、参考文献

基于模型预测控制的PMSM系统速度环控制理论推导及仿真搭建
永磁同步电机控制系统——模型预测控制（MPC）
模型预测控制简介（model predictive control）
永磁同步电机预测模型控制（MPC)

总结

本文仅仅简单介绍了【电机仿真】MPC控制器——PMSM有感FOC控制，评论区欢迎讨论。