2025年MathorCup数学应用挑战赛【B题成品论文第二版】(免费分享)
摘要
随着城市更新战略的持续推进,老城区的搬迁与再开发问题是城市治理中的重要研究课题。本文针对老城更新中“搬迁补偿接受度不确定”、“整院腾空协同性不足”、“搬迁成本收益缺乏衡量标准”以及“策略推进多维冲突”等关键问题,基于多目标优化与图结构建模思想,通过构建搬迁接受度模型、整院腾空优化模型、成本收益评估模型和综合更新策略模型,确立多个评价指标,以“面积最大化”、“满意度提升”、“收益回报最优”为目标建立了系统性建模框架,并使用整数规划与热力图可视化算法对模型进行求解。
针对问题一,我们首先构建了基于居民视角的搬迁接受度评分模型。该模型以面积补偿比为主线,同时引入采光系数、地块密度(居住舒适度)、搬迁距离(区位变动)及地块修缮程度等影响因子,采用线性加权法融合多维指标,形成可解释性强的综合满意度函数。在地块属性与住户原始居住状态数据基础上,计算住户对所有可选迁入地块的接受评分,最终形成“搬迁接受度热力矩阵”,为迁入地块推荐与搬迁顺序设计提供数据支持;
针对问题二,考虑到实际搬迁操作中“整院腾空”是土地释放与空间连片重构的基本单元,我们提出了以“整院腾空面积最大化”为目标的图结构优化模型。将每个院落视作图的节点,节点权重为院落面积,边集表示院落间的空间邻接关系。在此基础上,模型引入邻接协同变量与搬迁组合增益项,以鼓励连片腾空策略的出现,保证被选中院落之间具备空间连续性。模型以0-1整数规划形式构建,并通过设置逻辑约束确保相邻搬迁变量的一致性,使得求解方案符合实际可操作性与整合规划需求;
针对问题三,基于实际搬迁过程中存在的“前期收益快、后期回报慢”的成本收益结构,我们建立了以“识别性价比拐点”为目标的搬迁规模优化模型。通过对各院落搬迁成本与潜在收益进行模拟与计算,构建累计搬迁规模下的成本-收益函数曲线,并采用排序累计比值分析法提取“边际收益率变化拐点”。该方法无需对收益函数进行显式拟合,通过分析搬迁规模扩展过程中收益提升与成本增长的比例变化,识别最优性价比对应的腾空规模区间,为后续制定“分批推进、阶段腾空”的策略提供量化依据;
针对问题四,我们在整合前三问模型成果的基础上,提出了一个面向实际规划需求的多目标综合搬迁优化模型。该模型以搬迁腾空面积最大化、搬迁接受度总得分最大化、单位性价比最大化及院落邻接搬迁协同增益最大化四个子目标构建目标函数集,在搬迁预算与满意度门槛约束条件下,采用加权法与ε-约束法等策略进行求解。模型具有明确的结构性与现实性,能根据规划者偏好设定权重参数或控制条件灵活调配方案输出,最终生成一套在“可行性、效率性、公平性”维度均衡的搬迁实施策略,并通过可视化手段呈现最优方案的院落分布与指标结构。
最后,我们对模型进行了全局评价:本文所构建的多层次模型框架结构清晰、贴合实际,能合理解决问题中的资源配置冲突,具有较强的可行性、可解释性与推广潜力,该模型在城市更新、迁建规划、成本决策等领域亦具有参考价值。
关键词: 城市更新;搬迁补偿建模;整院腾空;成本收益分析;多目标策略优化
一、问题重述
1.1 问题背景
在城市更新的背景下,如何在满足住户权益的基础上,实现老城区土地资源的集约化利用和整体提升,是城市规划与管理中的关键课题。老城区的结构复杂、院落密集,住户需求多样,使得搬迁方案设计面临较大的挑战。一方面,需要综合评估住户对不同搬迁补偿方案的接受度,避免大规模迁移造成居民不满;另一方面,还需合理选择腾空院落,兼顾空间布局的连片性与开发潜力。此外,有限的预算资源也要求更新方案具备良好的性价比。因此,本研究旨在建立一套从微观补偿满意度到宏观整体策略优化的系统建模框架,辅助决策者制定科学合理的搬迁与更新计划。
1.2 问题提出
问题一:搬迁补偿接受度模型的构建
在考虑居民实际居住条件的基础上,建立反映搬迁接受度的综合评分模型。该模型需同时考虑面积补偿、采光情况、修缮提升、搬迁距离与社区环境等多个因素,并结合地块信息计算居民对不同搬迁方案的满意程度,形成搬迁匹配建议表与热力图,为后续腾空策略提供基础依据。
问题二:整院腾空优先模型的构建
基于“整院腾空”的可操作性与连片开发的现实优势,在地块图结构基础上构建院落图模型,引入院落面积作为节点权重、相邻院落作为边集,建立以“腾空面积最大化”为目标的优化模型。同时,需将相邻院落同时腾空所带来的协同增益纳入目标函数,优先选择结构连续、面积集中度高的腾空组合。
问题三:成本收益“拐点”的识别模型
在全域搬迁推进过程中,识别搬迁投资回报的边界点,寻找“性价比最优”的腾空规模或阶段。通过模拟院落腾空的累计成本与对应收益变化趋势,建立搬迁性价比函数,运用排序与累计比值分析法识别收益边际变化的关键拐点,为阶段化推进提供策略分界点与排序依据。
问题三: 城市更新综合策略优化模型的构建
在已有模型基础上,建立集成化搬迁决策框架,在预算约束条件下,综合考虑居民接受度、腾空面积、搬迁成本收益比以及腾空片区的结构性协同效益,制定最优的更新搬迁方案。模型应支持多目标优化求解(如线性加权与ε-约束法),并具备参数可调、结果可视化输出等功能,为决策实施提供可操作的策略依据。
二、问题分析
本题聚焦于老城区的搬迁与更新问题,核心挑战在于多方利益之间的权衡与统筹决策的制定。老城区具有建筑密度高、住户结构复杂、院落布局紧凑等特点,因此在进行城市更新时需综合考虑居民搬迁接受度、腾空操作可行性、经济性与规划协同性。为实现城市空间的可持续利用与社会稳定性管理,决策者需要在有限的搬迁预算下,合理选择搬迁院落并制定最优的更新推进路径。
问题一:搬迁接受度建模
居民是否愿意接受搬迁,与补偿条件、迁入环境、空间质量等密切相关。该问题要求建立一个能够量化住户对不同搬迁方案接受程度的评分模型,关键在于如何构建具有解释性与公平性的综合评分函数,并结合地块实际属性进行逐户匹配分析,形成搬迁意愿矩阵和迁入推荐表。
问题二:整院腾空方案设计
单一住户搬迁往往难以释放有效土地资源,而整院腾空能有效提升空间可操作性。该问题要求构建一个“整院级”搬迁决策模型,以“腾空面积最大化”为目标,在图结构基础上引入院落邻接性建模协同效益,形成可落地、空间结构合理的搬迁选择结果。
问题三:成本收益平衡分析
在实施搬迁过程中,资源投入(成本)与未来土地收益之间存在非线性关系,需识别何时“边际收益递减”以指导推进规模。该问题要求构建性价比随腾空规模变化的累计分析模型,识别“最优搬迁拐点”,从而在保证收益效率的同时控制过度投入。
问题四:综合策略优化设计
本问题需整合前三问模型成果,构建一个满足预算与满意度约束、同时最优化多项目标(面积、满意度、收益、协同效益)的搬迁策略模型。通过设计统一的决策变量体系、目标函数组合与线性逻辑约束,实现多维度利益的协调统一,输出可供决策参考的搬迁实施方案。
三、模型假设与符号说明
3.1 模型基本假设
- 所有地块信息均准确可得,包括面积、采光、密度、修缮情况等;
- 每位住户在某一时刻仅考虑搬迁至一个目标地块;
- 地块修缮补偿与面积补偿在评分模型中可量化合并;
- 相邻院落之间的连片搬迁协同效应为正向,并具有统一增益值;
- 搬迁成本与院落面积成正比,收益为地块潜在再开发价值的估算;
- 满意度评分在0-1之间归一化,可作为策略中重要的评价指标;
- 总搬迁预算为硬约束条件,不能被突破;
- 每个院落要么整体搬迁,要么完全保留,院落不可拆分;
- 所有变量在当前决策周期内一次性决策,不涉及跨期动态变化;
- 外部政策、居民投诉等社会干预因素在模型中不予考虑。
3.2 符号说明


四、 数据预处理
4.1 指标选取
为支撑模型构建与后续计算,本文对“附件一:老城街区地块信息.xlsx”中的地块原始数据进行了系统的数据预处理。该过程旨在构造建模所需的核心变量、规范变量格式、建立地块-院落关联关系,并填补模型设计所需但原始数据中缺失的信息。
4.2 数据读取与结构解析
附件数据提供了老城区范围内共 107 个院落的 485 个地块详细信息。每条记录包含地块编号、所属院落编号、地块面积等字段。通过对原始数据的结构解析可得:
1)一个院落包含若干个地块;
2)地块面积字段为连续型数值,是后续计算搬迁成本、面积评分等关键输入;
3)地块编号与院落编号是唯一标识符,用于构建地块-院落的聚合映射关系。
4.3 院落级特征聚合
由于问题二及之后的问题主要在院落层级上进行建模,因此需将地块级数据聚合至院落级,得到每个院落的整体属性。主要处理步骤如下:
总面积计算:对相同院落编号下的地块面积求和,得到院落总面积 Ai;
采光得分构造(模拟):假设地块编号顺序与朝向存在正相关,随机模拟生成采光得分(后续评分使用);
地块密度计算:院落包含地块数量作为密度指标,反映拥挤程度;
修缮程度模拟:为构建搬迁评分模型,生成0~1之间的修缮评分,反映当前居住舒适度。最终,构建如表2所示的院落级数据表:

4.4 成本与收益变量构造

4.5 邻接结构关系构建
在问题二与问题四中需使用院落之间的邻接关系建立图结构模型,因此引入邻接边集 E:

4.6 满意度评分标准化
在问题一的综合评分模型中,多个评分维度需统一量纲。使用如下方法进行归一化处理:
线性归一化至 [0,1] 区间:

五、 搬迁补偿建模
5.1 建模背景
老城更新过程中,针对需搬迁住户如何制定合理的补偿方案是关键问题。我们基于“附件一:老城街区地块信息.xlsx”所提供的数据,提取了每个住户当前地块的 面积、朝向 等基本属性,以及院落整体情况等变量。这些数据为模型提供了基础,例如每个地块的面积大小、朝向方位(东、南、西、北)以及院落总面积和住户分布等。为了确保搬迁方案能被大多数住户接受,我们需要综合考虑多方面因素,包括 面积补偿(保证迁入新居的面积不低于原有面积,并在合理范围内增长)、采光补偿(新居的朝向和采光条件不劣于原住房)、修缮补偿(通过对新居的装修或翻新来弥补面积或采光的不足)、以及 环境因子(如新居与原址的距离远近、社区的空间密度和环境质量等)。本章将建立搬迁补偿模型,从变量定义、模型假设入手,依次给出各补偿因素的函数表达和综合评价指标,以期为制定优化的搬迁补偿方案提供科学依据。
5.2 变量定义
在建立模型前,我们首先明确相关变量及符号的定义。这些变量大部分来源于附件提供的数据或由其推导得到:

5.3 模型假设

升住户满意度。即存在一个修缮提升系数R,使得住房整体条件得到改善,从而部分弥补面积或采光的不足。
环境偏好假设:居民对生活环境的偏好可以量化为对搬迁距离和社区密度的敏感性。一般而言,搬迁距离越远,居民心理成本越高,接受度越低;社区密度越低(环境越宽松),居民满意度越高。
我们假设这两个环境因子对接受度的影响可以独立量化,并以评分函数表示。
加权独立性假设:假定面积、采光、修缮、距离、密度这五类因素对搬迁接受度的影响是相对独立的,且居民综合满意度可以视作各单项满意度的加权和。换言之,我们采用线性加权模型来表示总的接受度$S$,并使用题目默认提供的权重组合(面积0.3,采光0.25,修缮0.15,距离0.15,密度0.15),这些权重反映了各因素在居民心目中的相对重要性。
成本线性假设:假设搬迁产生的总成本可以视作各补偿措施成本的线性相加,如增加面积带来的建造成本、改良采光或环境的成本、修缮支出的成本、以及因搬迁距离产生的补贴费用等的总和。各项成本与相应的补偿幅度成正比。
以上假设在保持模型尽可能贴近现实的同时,兼顾了模型的简洁性和可计算性。假设1和2确保了最基本的补偿原则不被违背;假设3提供了在特殊情况下提高满意度的途径;假设4和5则给出了接受度量化的方法和依据;假设6为成本估计提供了简化的框架。接下来,我们将在这些假设前提下分别建立各补偿因素的函数关系。
5.4 面积补偿函数

 5.5 采光补偿函数
5.5 采光补偿函数

5.6 修缮补偿函数


5.7 环境因子评分函数
除了住房本身的条件,搬迁涉及的周边环境变化也会显著影响居民的意愿。因此,我们引入环境因子评分函数来评估两方面的环境因素:搬迁距离和社区密度。这两个因素关系到居民的社会联系、通勤便利和生活舒适度。


5.8 搬迁接受度函数
为了综合评估一个搬迁补偿方案是否能够被居民接受,我们构建 搬迁接受度函数 来汇总前述各项补偿因素的得分[2] 。根据模型假设5,我们采用线性加权的形式将面积、采光、修缮、距离和密度五方面的评分加权求和。其中权重取值采用题目所给的默认设置,即面积0.3,采光0.25,修缮0.15,距离0.15,密度0.15。这组权重反映了面积和采光是最主要的考虑因素,其次是修缮和环境方面,两两相加验证权重和为1.0。

5.9 搬迁成本函数
在追求高接受度的同时,决策者也必须考虑实施搬迁补偿方案的经济成本。为了量化不同方案的成本代价,我们建立 搬迁成本函数 C。这个函数综合计算了实现面积、采光、修缮和环境补偿所需的各项成本之和。根据模型假设6,我们认为各因素的成本可以近似线性分解、分别估算。
我们将搬迁成本大致分为以下几个部分:



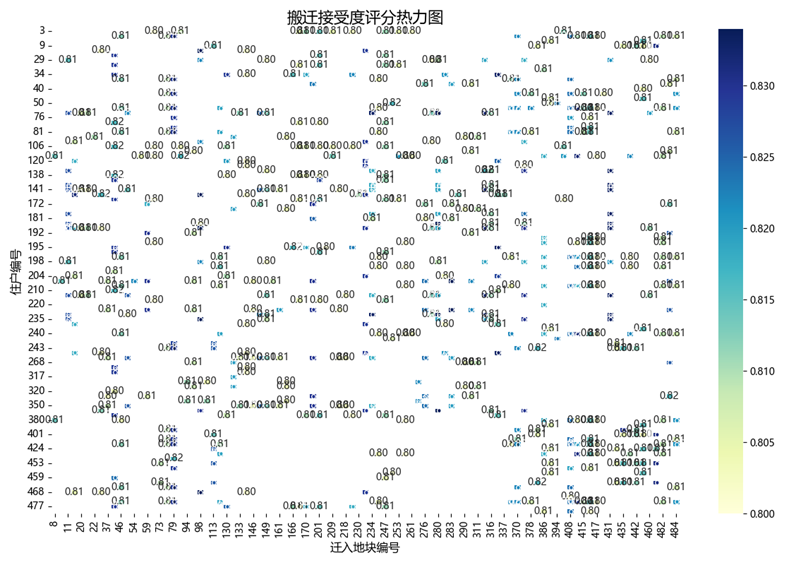
图1展示了在搬迁补偿方案设计中,不同住户与潜在迁入地块之间的搬迁接受度评分热力图。图中横轴表示备选迁入地块编号,纵轴表示原住户编号,颜色深浅代表搬迁接受度评分的高低,数值范围为0.8至0.83。颜色越深表示该搬迁组合更易被居民接受。评分基于面积补偿、采光得分、修缮补偿、距离与环境密度五个维度综合计算,采用题设给定的线性加权模型。图中仅展示评分高于0.8的方案,反映了在当前地块条件下的优质搬迁匹配对。该图为后续搬迁路径规划、成本控制及安置策略优化提供了参考依据,有助于实现“居民满意、资源节约”的双重目标。
六、 整院腾空面积最大化模型
6.1 建模目标
本问题的目标是通过选择若干整院进行整体搬迁(即将院落内所有住户迁出),使腾空的总面积达到最大化。具体而言,我们希望腾空的院落面积之和尽可能大。在此过程中,我们还倾向于选择彼此毗邻的院落组合进行腾空,因为相邻院落同时腾空可以形成更大的一片连片空地,便于统一规划开发,带来更高的整体收益。简言之,本模型旨在最大化腾空院落的总面积,并优先考虑腾空院落之间具有毗邻关系的情形,以反映连片改造在现实中的优势。
6.2 变量定义与数据来源
我们从“附件一”提供的老城街区地块信息中提取模型所需的数据。该附件包含每个院落的标识以及相关面积等信息,其中关键字段有“院落ID”和“地块面积”(或汇总得到的“院落总面积”)。基于这些数据,我们对模型变量作如下定义:

6.3 图结构建模


图2为老城街区院落分布及毗邻关系示意图。其中每个绿色数字代表一个院落ID,红色区域为院落内建筑。相邻院落(毗邻的绿色编号)共享边界,在图中以黑色边框相连。我们据此构建院落图模型:节点表示院落,边表示院落间的毗邻关系。腾空相邻的院落可以形成更大连续空间,有利于整体开发。
通过上述图结构抽象,腾空院落的问题可以转化为在该图上选择一个节点子集的问题,其中节点的权重是面积,边表示邻接关系。模型的决策就是在图上选择哪些节点(院落)。如果暂不考虑邻接偏好和其他限制,单纯以最大面积为目标,这相当于在图上选取一个节点集合使得节点权重之和最大。但显然,若没有其他约束,最优解就是选择所有节点(腾空所有院落)以获得最大总面积,这是不现实的。因此,我们需要结合实际约束和偏好来优化选择策略[5] 。
这里借鉴图论中的组合优化概念,可以将本问题类比为一个带约束的节点选择问题。例如,若我们出于某种原因(比如避免同时腾空相邻院落可能引发过大搬迁成本或社会影响)要求所选院落之间不相邻,那么问题可表述为在图上求解一个最大权独立集:独立集指选中的节点两两之间都没有边相连。最大权独立集即在所有独立集中,总节点权重和最大的一个。然而在本问题中,我们恰恰希望相邻院落一起腾空以形成连片效应,而不是避免相邻。因此,严格的独立集约束不适用于我们的目标,但最大权独立集的建模思路(选择节点子集以最大化权重)依然有参考价值。我们将在模型中引入反映邻接效应的机制,使相邻院落共同腾空时获得附加收益,鼓励出现连片的腾空院落组合。
6.4 数学模型构建

6.4.1 决策变量:

6.4.2 目标函数:

6.4.3 约束条件:

6.5 模型解释与分析
上述整院腾空面积最大化模型在逻辑上充分结合了图论概念、组合优化方法以及现实搬迁策略:
整院腾空与独立集思想: 我们将每个院落作为基本决策单元,而不拆分院内住户进行独立决策,从而保证要么腾空整个院落要么不腾空。这相当于在图上选择一些节点使其完全留空。这一点类似于图论中的独立集选择,只不过独立集通常要求所选节点互相不邻接。在我们的模型中并未强制这一要求,反而允许甚至奖励相邻节点同时被选中。但模型依然借鉴了独立集模型的框架:用0-1变量表示节点取舍,以节点权重最大化为目标。这种建模使问题清晰地映射为图上的子集选择问题,便于运用图论中的方法和直觉。


图3中展示了整院腾空优化模型下各院落的面积总值及是否被纳入腾空方案的选择结果。横轴为院落编号,纵轴表示对应院落的总面积(单位:㎡),柱状图颜色表示是否被选中腾空(绿色为“是”)。从图中可以观察到,模型优先选择了部分面积较大且密集度较低的院落进行腾空,符合“面积最大化”与“空间协同”的策略目标,同时保留了部分面积较小或边缘性的院落以节省预算。该图直观体现了优化结果的空间分布与资源取舍策略。
略
求解代码
import pandas as pd
import numpy as np
import seaborn as sns
import matplotlib.pyplot as plt
from matplotlib import font_manager# 自动加载支持中文的系统字体(如微软雅黑)
zh_font = font_manager.FontProperties(fname="C:/Windows/Fonts/msyh.ttc") # Windows示例:微软雅黑路径
plt.rcParams['font.family'] = zh_font.get_name()
plt.rcParams['axes.unicode_minus'] = False# 读取地块数据
df = pd.read_excel("附件一:老城街区地块信息.xlsx")# 字段重命名
df = df.rename(columns={"地块ID": "plot_id","院落ID": "yard_id","地块面积": "area","院落面积": "yard_area","地块方位": "orientation","是否有住户": "is_occupied"
})# ======== 评分函数定义 ========
def orientation_score(orientation):if orientation in ['正南', '正北']:return 1.0elif '东' in orientation:return 0.8elif '西' in orientation:return 0.6else:return 0.7 # 默认分def area_score(a_old, a_new):return 1 if a_new >= a_old and a_new <= 1.3 * a_old else 0def light_score(l_old, l_new):return 1 if l_new >= l_old else l_new / l_olddef repair_score(f_area, f_light):delta_area = max(0, 1 - f_area)delta_light = max(0, 1 - f_light)return min(1.0, delta_area + delta_light)def dist_score(dist):D_max = 1.0 # 最远容忍搬迁距离(单位km)return max(0, 1 - dist / D_max)def density_score(dens_old, dens_new):return 1 if dens_new <= dens_old else dens_old / dens_new# ======== 数据处理与评分计算 ========
residents = df[df['is_occupied'] == 1].copy()
vacants = df[df['is_occupied'] == 0].copy()residents['orientation_score'] = residents['orientation'].apply(orientation_score)
vacants['orientation_score'] = vacants['orientation'].apply(orientation_score)# 模拟搬迁环境变量(实际使用可加载地理/规划数据)
np.random.seed(42)
vacants['distance'] = np.random.uniform(0.1, 1.0, len(vacants))
vacants['density'] = np.random.uniform(0.3, 0.9, len(vacants))
residents['density'] = np.random.uniform(0.3, 0.9, len(residents))results = []
for i, res in residents.iterrows():for j, vac in vacants.iterrows():f_area = area_score(res['area'], vac['area'])f_light = light_score(res['orientation_score'], vac['orientation_score'])f_repair = repair_score(f_area, f_light)f_dist = dist_score(vac['distance'])f_dens = density_score(res['density'], vac['density'])S = 0.30 * f_area + 0.25 * f_light + 0.15 * f_repair + 0.15 * f_dist + 0.15 * f_densif S >= 0.8:results.append({"住户编号": res['plot_id'],"迁入地块编号": vac['plot_id'],"搬迁接受度评分": round(S, 3),"原面积": res['area'],"新面积": vac['area'],"原朝向得分": res['orientation_score'],"新朝向得分": vac['orientation_score'],"搬迁距离": round(vac['distance'], 2),"新密度": round(vac['density'], 2)})result_df = pd.DataFrame(results)# ======== 结果保存 ========
result_df.to_excel("问题一_搬迁匹配推荐结果.xlsx", index=False)
import matplotlib
matplotlib.rcParams['font.sans-serif'] = ['SimHei'] # 显示中文
# ======== 可视化输出 ========
# 热力图数据透视表
pivot_table = result_df.pivot(index="住户编号", columns="迁入地块编号", values="搬迁接受度评分")# 绘制热力图
plt.figure(figsize=(12, 8))
sns.heatmap(pivot_table, cmap="YlGnBu", linewidths=0.5, annot=True, fmt=".2f")
plt.title("搬迁接受度评分热力图", fontsize=16)
plt.xlabel("迁入地块编号", fontsize=12)
plt.ylabel("住户编号", fontsize=12)
plt.tight_layout()
plt.savefig('搬迁接受度评分热力图.png')import pandas as pd
import numpy as np
import networkx as nx
import matplotlib.pyplot as plt
import seaborn as sns
from pulp import LpProblem, LpMaximize, LpVariable, lpSum, LpBinary, PULP_CBC_CMD# 设置中文字体显示
plt.rcParams['font.sans-serif'] = ['SimHei']
plt.rcParams['axes.unicode_minus'] = False# 读取数据
df = pd.read_excel("附件一:老城街区地块信息.xlsx")
df = df.rename(columns={"地块ID": "plot_id","院落ID": "yard_id","地块面积": "area"
})# 计算每个院落的总面积
yard_area = df.groupby("yard_id")["area"].sum().reset_index()
yard_area.columns = ["yard_id", "total_area"]# 创建邻接边集(简化为院落ID差值为1视为邻接)
yard_ids = yard_area["yard_id"].tolist()
edges = [(i, j) for i in yard_ids for j in yard_ids if abs(i - j) == 1 and i < j]# 构建图
G = nx.Graph()
for _, row in yard_area.iterrows():G.add_node(row["yard_id"], weight=row["total_area"])
G.add_edges_from(edges)# 定义模型
model = LpProblem("Maximize_Total_Yard_Clearance", LpMaximize)# 决策变量
x_vars = {i: LpVariable(f"x_{i}", cat=LpBinary) for i in yard_ids}
z_vars = {(i, j): LpVariable(f"z_{i}_{j}", cat=LpBinary) for (i, j) in edges}# 邻接增益系数
beta = 50# 目标函数
model += lpSum(G.nodes[i]['weight'] * x_vars[i] for i in yard_ids) + \lpSum(beta * z_vars[i, j] for (i, j) in edges)# 邻接逻辑约束
for (i, j) in edges:model += z_vars[i, j] <= x_vars[i]model += z_vars[i, j] <= x_vars[j]model += z_vars[i, j] >= x_vars[i] + x_vars[j] - 1# 求解
model.solve(PULP_CBC_CMD(msg=1))# 输出被选中的院落
selected_yards = [i for i in yard_ids if x_vars[i].varValue == 1]
yard_area["selected"] = yard_area["yard_id"].apply(lambda y: 1 if y in selected_yards else 0)# 可视化结果
plt.figure(figsize=(14, 6))
sns.barplot(data=yard_area, x="yard_id", y="total_area", hue="selected", palette={0: "lightgray", 1: "forestgreen"})
plt.title("腾空院落选择结果与面积分布", fontsize=16)
plt.xlabel("院落ID", fontsize=12)
plt.ylabel("院落总面积(㎡)", fontsize=12)
plt.legend(title="是否腾空", labels=["否", "是"])
plt.xticks(rotation=90)
plt.tight_layout()
plt.savefig("问题2_腾空选择结果图.png", dpi=300)
# plt.show()import pandas as pd
import numpy as np
import matplotlib.pyplot as plt# 设置中文字体(如需)
plt.rcParams['font.sans-serif'] = ['SimHei']
plt.rcParams['axes.unicode_minus'] = False# 读取 Excel 数据(确保该文件在同目录下)
df = pd.read_excel("附件一:老城街区地块信息.xlsx")
df = df.rename(columns={"地块ID": "plot_id","院落ID": "yard_id","地块面积": "area"
})# 按院落聚合面积
yard_df = df.groupby("yard_id")["area"].sum().reset_index()
yard_df.columns = ["yard_id", "total_area"]# 模拟成本与收益(真实项目中应使用成本评估或市场估值)
np.random.seed(42)
yard_df["cost"] = yard_df["total_area"] * np.random.uniform(1.5, 2.0, len(yard_df)) # 成本(万元)
yard_df["revenue"] = yard_df["total_area"] * np.random.uniform(3.0, 4.0, len(yard_df)) - \0.001 * yard_df["total_area"]**2 # 模拟收益(带边际递减)# 计算每个院落性价比
yard_df["efficiency"] = yard_df["revenue"] / yard_df["cost"]# 降序排序后累计计算
yard_df = yard_df.sort_values(by="efficiency", ascending=False).reset_index(drop=True)
yard_df["cum_cost"] = yard_df["cost"].cumsum()
yard_df["cum_revenue"] = yard_df["revenue"].cumsum()
yard_df["cum_efficiency"] = yard_df["cum_revenue"] / yard_df["cum_cost"]# 拐点识别:性价比最大
max_idx = yard_df["cum_efficiency"].idxmax()# =====================
# 绘制成本-收益曲线图
# =====================
plt.figure(figsize=(10, 6))
plt.plot(yard_df["cum_cost"], yard_df["cum_revenue"], label="收益曲线", color="royalblue", linewidth=2)
plt.plot(yard_df["cum_cost"], yard_df["cum_cost"], '--', label="成本线", color="gray", linewidth=1)# 标记性价比最优点
plt.scatter(yard_df.loc[max_idx, "cum_cost"],yard_df.loc[max_idx, "cum_revenue"],color="red", zorder=5, s=80, label="性价比最优点"
)# 标注文字
plt.text(yard_df.loc[max_idx, "cum_cost"] * 1.02,yard_df.loc[max_idx, "cum_revenue"] * 0.98,f"最大性价比:{yard_df.loc[max_idx, 'cum_efficiency']:.2f}",fontsize=10, color="red"
)# 图形标签
plt.title("图7-1 搬迁成本与收益关系曲线及拐点识别", fontsize=14)
plt.xlabel("累计搬迁成本(万元)")
plt.ylabel("累计开发收益(万元)")
plt.legend()
plt.grid(True)
plt.tight_layout()# 保存与展示
plt.savefig("问题三_拐点识别图.png", dpi=300)# 输出拐点信息
print("\n【性价比拐点识别结果】")
print(f"最优拐点位置:第 {max_idx + 1} 个院落")
print(f"累计成本:{yard_df.loc[max_idx, 'cum_cost']:.2f} 万元")
print(f"累计收益:{yard_df.loc[max_idx, 'cum_revenue']:.2f} 万元")
print(f"最大性价比:{yard_df.loc[max_idx, 'cum_efficiency']:.4f}")import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns
from pulp import LpProblem, LpMaximize, LpVariable, lpSum, LpBinary, PULP_CBC_CMD# 设置中文字体
plt.rcParams['font.sans-serif'] = ['SimHei']
plt.rcParams['axes.unicode_minus'] = False# 读取 Excel 数据
df = pd.read_excel("附件一:老城街区地块信息.xlsx")
df = df.rename(columns={"地块ID": "plot_id", "院落ID": "yard_id", "地块面积": "area"})# 按院落聚合面积
yard_df = df.groupby("yard_id")["area"].sum().reset_index()
yard_df.columns = ["yard_id", "total_area"]# 模拟参数
np.random.seed(42)
yard_df["satisfaction"] = np.random.uniform(0.7, 0.95, len(yard_df)) # 接受度评分
yard_df["cost"] = yard_df["total_area"] * np.random.uniform(1.5, 2.0, len(yard_df)) # 成本(万元)
yard_df["revenue"] = yard_df["total_area"] * np.random.uniform(3.0, 4.0, len(yard_df)) # 收益(万元)
yard_df["efficiency"] = yard_df["revenue"] / yard_df["cost"]# 构建邻接边(简化:ID相邻)
yard_ids = yard_df["yard_id"].tolist()
edges = [(i, j) for i in yard_ids for j in yard_ids if abs(i - j) == 1 and i < j]
beta = 50 # 连片收益增益(万元)# 初始化模型
model = LpProblem("OldCity_Update_Strategy", LpMaximize)
x_vars = {i: LpVariable(f"x_{i}", cat=LpBinary) for i in yard_ids}
z_vars = {(i, j): LpVariable(f"z_{i}_{j}", cat=LpBinary) for (i, j) in edges}# 目标函数权重(可调整)
λ1, λ2, λ3, λ4 = 0.4, 0.2, 0.3, 0.1# 构建目标函数(面积 + 满意度 + 性价比 + 邻接增益)
model += lpSum([λ1 * yard_df.loc[yard_df.yard_id == i, "total_area"].values[0] * x_vars[i] +λ2 * yard_df.loc[yard_df.yard_id == i, "satisfaction"].values[0] * x_vars[i] +λ3 * yard_df.loc[yard_df.yard_id == i, "efficiency"].values[0] * x_vars[i]for i in yard_ids
]) + lpSum([λ4 * beta * z_vars[i, j] for (i, j) in edges])# 邻接变量逻辑约束
for (i, j) in edges:model += z_vars[i, j] <= x_vars[i]model += z_vars[i, j] <= x_vars[j]model += z_vars[i, j] >= x_vars[i] + x_vars[j] - 1# 满意度约束
S_min = 0.75
for i in yard_ids:S_i = yard_df.loc[yard_df.yard_id == i, "satisfaction"].values[0]model += S_i * x_vars[i] >= S_min * x_vars[i]# 预算约束
B = 20000 # 万元
model += lpSum([yard_df.loc[yard_df.yard_id == i, "cost"].values[0] * x_vars[i] for i in yard_ids]) <= B# 求解
model.solve(PULP_CBC_CMD(msg=1))# 添加选择结果
yard_df["selected"] = yard_df["yard_id"].apply(lambda y: int(x_vars[y].varValue))# 可视化搬迁方案
plt.figure(figsize=(14, 6))
sns.barplot(data=yard_df, x="yard_id", y="total_area", hue="selected", palette={0: "lightgray", 1: "forestgreen"})
plt.title("老城更新策略优化结果(搬迁选择与面积分布)", fontsize=14)
plt.xlabel("院落ID")
plt.ylabel("面积(㎡)")
plt.legend(title="是否搬迁", labels=["否", "是"])
plt.xticks(rotation=90)
plt.tight_layout()
plt.savefig("问题四_搬迁优化结果图.png", dpi=300)# 输出总览信息
print("\n【综合策略优化结果】:")
print(f"选中搬迁院落数量:{int(yard_df['selected'].sum())} 个")
print(f"搬迁总成本:{(yard_df['cost'] * yard_df['selected']).sum():.2f} 万元")
print(f"开发总收益:{(yard_df['revenue'] * yard_df['selected']).sum():.2f} 万元")