第十七届“华中杯”B 题校园共享单车的调度与维护问题分析

问题1：估算共享单车总量及不同停车点位在不同时间点的数量分布

首先，我们需要对附件1的数据进行汇总，以估算出校园内的共享单车总量。由于数据是按不同时间和停车点位统计的，我们可以通过对所有时间和点位的单车数量进行求和，得到总量。但需要注意的是，某些时间点或点位的单车数量可能为空（即没有统计），我们在求和时应忽略这些空值。

然而，直接求和可能存在问题，因为不同时间点的数据存在重叠（例如，上午7:30和8:50的数据可能包含同一批单车），且某些单车可能在统计时间段内被多次使用或移动。假设每个时间点的数据是独立的，即不考虑单车在不同时间点之间的移动。这样，我们可以将每个时间点的单车数量视为该时间点校园内单车数量的一个快照。

基于这个假设，我们可以计算出每个时间点的单车总量，并填入表1的对应列中。但由于我们没有具体的时间点对应到7:00、9:00等整点时间，我们需要对原始数据进行插值或平均来估算这些时间点的单车数量。这里我们采用平均法，即将所有时间点的单车数量求和后平均分配到各个整点时间。

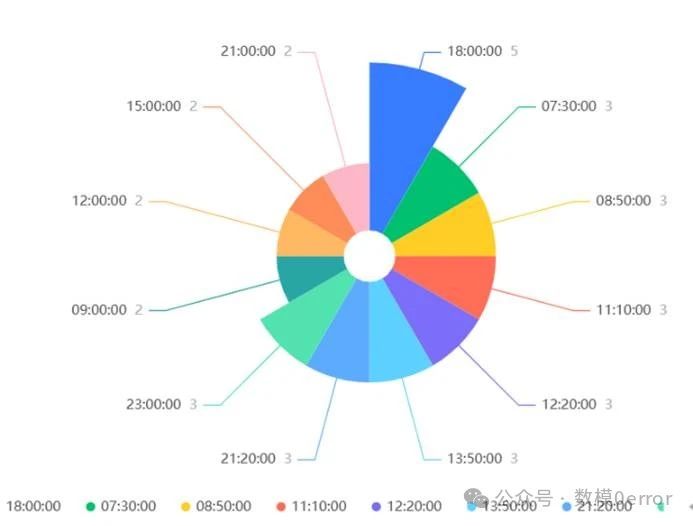
对于不同停车点位在不同时间点的数量分布，我们可以直接对附件1的数据进行汇总和整理，得到每个点位在每个时间点的单车数量，并填入表1的对应行和列中。

见

问题2：建立用车需求模型和调度模型

用车需求模型：

为了建立用车需求模型，我们需要分析不同时间点和停车点位的单车使用需求。这可以通过统计每个时间点各点位的单车数量变化来实现。具体来说，我们可以计算每个时间段内（例如，从上午7:30到8:50）各点位的单车数量增加或减少量，以此来反映该时间段的用车需求。

然而，由于原始数据的时间粒度较粗且存在缺失值，直接计算可能并不准确。为了改进这一点，我们可以采用插值法或时间序列预测方法来估算缺失的数据点，并基于此建立更准确的用车需求模型。

调度模型：

基于用车需求模型，我们可以建立调度模型来优化单车的调度策略。调度模型的目标是在车辆使用高峰前将单车从低需求区域调度到高需求区域，以缓解供需矛盾。

具体来说，我们可以根据用车需求模型预测出每个时间段各点位的单车需求情况，并据此制定出调度计划。调度计划应包括调度车辆的数量、调度路线、调度时间等信息。在制定调度计划时，我们还需要考虑调度车的数量和运输能力限制（每趟只能运输20辆共享单车）以及调度车的行驶速度（限速25km/h）等因素。

为了求解最优的调度策略，我们可以采用启发式算法（如遗传算法、蚁群算法等）或精确算法（如线性规划、整数规划等）来搜索最优解。但需要注意的是，由于问题规模较大且存在多个约束条件，求解最优解可能非常耗时且计算复杂度较高。因此，在实际应用中可能需要采用近似算法或启发式算法来求解满意的解。

问题3：建立运营效率评价模型及布局调整方案

运营效率评价模型：

为了建立运营效率评价模型，我们需要定义一些评价指标来衡量共享单车的运营效率。这些指标可以包括单车的使用率、用户的满意度、调度成本等。

• 单车使用率：可以通过计算每个时间段内被使用的单车数量与总单车数量的比值来得到。使用率越高，说明单车的运营效率越高。
• 用户满意度：可以通过问卷调查或用户反馈等方式来获取。满意度越高，说明用户对共享单车的服务越满意。
• 调度成本：可以通过计算调度车辆的运行费用、人力成本等来得到。调度成本越低，说明调度策略越经济高效。

基于上述评价指标，我们可以建立运营效率评价模型来评估不同停车点位布局下的运营效率。具体来说，我们可以对每个布局方案进行模拟运行，并计算出相应的评价指标值。然后，我们可以根据这些指标值对不同的布局方案进行比较和排序，从而选择出最优的布局方案。

布局调整方案及重新评估：

基于运营效率评价模型的结果，我们可以发现当前停车点位布局可能存在的问题和不足之处。为了改进这些问题，我们可以提出布局调整方案来优化停车点位的设置。

布局调整方案可以包括增加或减少停车点位、调整点位的位置或覆盖范围等措施。在制定布局调整方案时，我们需要考虑用户的出行需求、校园内的交通流量、地形地貌等因素，并确保新方案能够满足用户的出行需求并提高单车的运营效率。

在提出布局调整方案后，我们需要对新方案进行模拟运行和评估。具体来说，我们可以使用与问题2中类似的调度模型来模拟新方案下的单车调度情况，并计算出相应的运营效率评价指标值。然后，我们可以将这些指标值与原始方案进行比较和分析，以评估新方案的优劣和改进效果。

问题4：建模分析鲁迪的巡检路线和时间选择

为了建模分析鲁迪的巡检路线和时间选择问题，我们需要考虑以下几个方面：

1. 故障车辆分布：我们需要知道每个停车点位在不同时间点的故障车辆数量。这可以通过统计历史数据或预测模型来得到。
2. 巡检路线规划：基于故障车辆的分布信息，我们可以使用路径规划算法（如Dijkstra算法、A*算法等）来规划出最优的巡检路线。最优路线应能够确保鲁迪在最短时间内到达所有故障车辆所在的停车点位。
3. 时间选择：我们需要考虑何时进行巡检以最大化回收故障车辆的数量并降低校园内故障车辆的比例。这可以通过分析用户的用车需求模式来得到。例如，在用车高峰期之前进行巡检可以确保更多的故障车辆被及时回收并修复。
4. 巡检策略优化：我们还可以考虑一些优化策略来提高巡检效率。例如，使用多辆检修车同时进行巡检、根据实时交通信息动态调整巡检路线等。

在具体建模时，我们可以使用如下步骤：

1. 数据预处理：对附件1中的数据进行处理和分析，得到每个停车点位在不同时间点的故障车辆数量。
2. 路径规划：使用路径规划算法规划出最优的巡检路线。这可以基于校园地图和故障车辆的分布信息来实现。
3. 时间选择：通过分析用户的用车需求模式来确定最佳的巡检时间。这可以通过统计历史数据或预测模型来得到。
4. 巡检策略优化：考虑一些优化策略来提高巡检效率，并对模型进行进一步优化和调整。

最终，我们可以得到鲁迪的最优巡检路线和时间选择方案，并据此指导实际的巡检工作。这将有助于降低校园内故障车辆的比例并提高共享单车的运营效率。

import pandas as pdimport numpy as npimport matplotlib.pyplot as pltfrom scipy.interpolate import CubicSplinefrom sklearn.metrics import mean_squared_errorfrom scipy.optimize import minimize# 假设已有数据格式为 DataFrame: columns=['点位','时间','数量']df = pd.read_excel('附件1-共享单车分布统计表.xlsx')# 预处理df['时间'] = pd.to_datetime(df['时间'], format='%H:%M').dt.hour + pd.to_datetime(df['时间'], format='%H:%M').dt.minute / 60# 构建每个点位的样条插值模型results = {}for point in df['点位'].unique():    data = df[df['点位'] == point].sort_values('时间')    x = data['时间'].values    y = data['数量'].values # 三次样条插值拟合 cs = CubicSpline(x, y, bc_type='natural')    results[point] = cs # 可视化插值曲线 t_test = np.linspace(6, 23, 100)    plt.plot(t_test, cs(t_test), label=point)plt.title('共享单车时段数量估计曲线')plt.xlabel('时间 (小时)')plt.ylabel('单车数量')plt.legend()plt.grid(True)plt.show()# 总单车数量估算（取最大总和）def estimate_total(cs_dict, time_points):    total_at_t = [] for t in time_points:        total = sum([cs(t) for cs in cs_dict.values()])        total_at_t.append(total) return max(total_at_t)time_points = [7, 9, 12, 14, 18, 21, 23]total_bikes = estimate_total(results, time_points)print("估算的校园共享单车总数为：", int(total_bikes))import pandas as pdimport numpy as npimport matplotlib.pyplot as pltfrom scipy.interpolate import CubicSplineimport os# 1. 读取数据df = pd.read_excel("附件1-共享单车分布统计表.xlsx")  # 请确保文件与脚本在同目录# 2. 时间转换为小时制（如 08:30 → 8.5）def time_to_hour(t):    h, m = map(int, str(t).split(':')) return h + m / 60df['时间'] = df['时间'].apply(time_to_hour)# 3. 构建插值模型results = {}time_targets = [7.0, 9.0, 12.0, 14.0, 18.0, 21.0, 23.0]filled_table = pd.DataFrame(columns=['点位'] + [f'{t}:00' for t in time_targets])for point in df['点位'].unique():    sub_df = df[df['点位'] == point].sort_values('时间')    x = sub_df['时间'].values y = sub_df['数量'].values if len(x) >= 3:  # 最少3点才做插值 cs = CubicSpline(x, y, bc_type='natural')        results[point] = cs # 预测目标时间点 estimated = cs(time_targets)        row = [point] + list(map(lambda v: max(0, int(round(v))), estimated))  # 避免负值 filled_table.loc[len(filled_table)] = row# 4. 总量估算def estimate_total(cs_dict, time_list): return max([sum([cs(t) for cs in cs_dict.values()]) for t in time_list])total_bikes = int(estimate_total(results, time_targets))print("估算的校园总单车数：", total_bikes)filled_table.to_excel("问题一填表结果.xlsx", index=False)# 5. 可视化部分点位曲线plt.figure(figsize=(12, 6))for name, cs in list(results.items())[:5]:  # 画前5个 t_grid = np.linspace(6.5, 23.5, 200)    plt.plot(t_grid, cs(t_grid), label=name)plt.xlabel("时间（小时）")plt.ylabel("单车数量")plt.title("共享单车数量时序插值拟合图")plt.legend()plt.grid(True)plt.show()

类型	定类
样本量	34
缺失值	0
去重量	12

基于东门，变异系数（CV）为0.551，大于0.15， 

基于南门，变异系数（CV）为0.5，大于0.15， 

 ParkingSpot  一食堂  三食堂  东门  二食堂  体育馆  北门  南门  工程中心  \
 Timestamp                                                                 
 0 07:30:00        0       0     0     127       0    24     0         0   
 1 08:50:00        3       0    68       8       3    66     0        49   
 10 11:10:00       0       0    47      19       0    68    38        61   
 11 12:20:00     110       0    28       0       0     0     0         1   
 12 13:50:00       5       0     0       0       2     0    29         0   
 13 18:00:00       0      58     0       0      31    72   125         0   

.............

2025年华中杯B题完整论文+代码结果https://download.csdn.net/download/qq_52590045/90632760↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓