总结【过往部分项目经历一(计算机图形学方向)】
总结【过往部分项目经历】
- 1.蜂窝填充算法
- 2.孔洞识别算法
- 3.扫掠轮廓计算
- 4.二维排料算法
- 5.最大内接圆算法
1.蜂窝填充算法
介绍: 主要从二维六角网格基本算法出发,基于自定义数据结构和拓扑关系,从二维到三维进行拓展,六角网格->六棱柱->带孔六棱柱->基于空间关系的蜂窝。
二维六角网格算法原理,参考博客六角网格大观,借助到里面的三轴坐标系统。



从二维到三维的延拓,使用自定义数据结构和拓扑关系(技术细节不便展示)。



2.孔洞识别算法
介绍: 对于破损的网格表面,有时需要精准找到对应孔洞进行修复和网格重建。所以实现孔洞识别算法是后续过程的必经之路。
结果显示:自定义算法识别准确率达到工业级软件Materialise Magics官网同等效果。

整体效果,找到所有的孔洞,每个孔洞都为一个闭环链路,且环与环之间不存在相交,但可共顶点或共边。

对于复杂的孔洞边界也能精准识别,而且算法复杂度为 O ( l o g N ) O(logN) O(logN),也是比较低的。


找到第3个孔洞,第4个孔洞情形:


第5个孔洞,第6个孔洞情形:


3.扫掠轮廓计算
介绍: 空间一固定多边形PFA(红色表示),和一个只做平移运动的多边形PMB(绿色表示),还有一动点p,p和多边形PMB相对位置保持不变。当p在多边形PFA边界运动一周后,连动的多边形PMB扫掠出一个外围多边形(蓝色多边形即为最终结果)



将运动多边形拓展为更一般的凹多边形,算法也更具备一般性。


4.二维排料算法
介绍: 在特定空间(可以为矩形或任意多边形轮廓内),将多个多边形作为待摆放样件,使两两之间不重叠,同时尽可能紧凑,空间利用率尽可能较高。

排样时是用到一种NFP算法,当时参考的是知网这篇博士基于临界多边形的二维排样算法研究,这个算法实现比较复杂。自己测试中发现了部分解 和退化解特殊情形,虽然项目落地后不容易测到,也算是该算法一个小缺陷吧。




和行业标杆软件VoxelDance对比:
在旋转步长为20度的情况下,和tango对比情况。


在旋转步长为20度的情况下,和tango对比情况。


5.最大内接圆算法
介绍: 任意多边形轮廓(可以是凹的,带多个孔洞的),计算其内部最大内接圆。

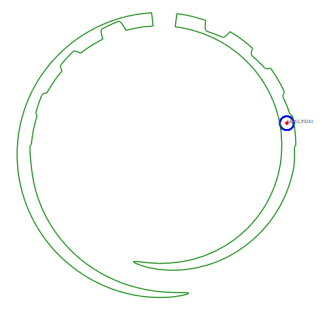


相比较于泊松采样,条件采样,以及四分法,计算效率明显出现几十倍地提升。



