当前位置：首页 > news >正文

卡尔曼滤波-从公式到理解

news 来源：原创 2025/5/21 1:17:35

参考文献：

【卡尔曼滤波】图文结合带你详细推导卡尔曼滤波（超详解）-CSDN博客

本文基于上述参考文献，进行进一步的理解。

卡尔曼滤波是将预测的值和量测的值结合起来，获得更接近真实情况的数值。

目前，我的理解只能在文中举的一个特定的例子上，即：预测一个机器人的某一时刻的速度和位置，下面的描述均以这个例子为例进行说明。

预测值是指机器人的速度和位置

已知当前的机器人的位置和速度，机器人下一时刻的速度和位置可以通过一个模型计算出来，这里可以通过，加速度对时间的积分获得速度，通过对速度的积分获得位置。因此，从公式上可以写为：

x_k 表示的是k时刻的预测值，包含了p位置和v速度两个值。

P_k表示的是p和v的协方差，协方差是两个变量的相关性。

表示的是p和v的更新公式，即k时刻的p和v与k-1时刻的p和v之间的关系。

这里，把上面的方程表示为矩阵的形式，则F_k表示的是预测矩阵，矩阵只是计算上的便利和表达形式上的简化而已，并没有特别多的作用。

如果变量的转移矩阵为F_k，根据上面的协方差矩阵特性，新的协方差矩阵可以表示为：

这个公式就是，需要预测的变量k-1时刻与k时刻的关系，同时，其协方差矩阵也发生了变化。

注意，上面的p和v的更新是不合理的，更合理地应该写为：

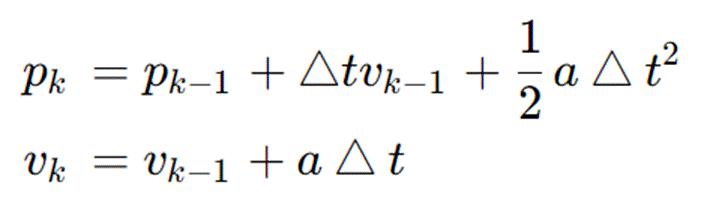
因此，其转换矩阵（将上面的公式写成矩阵的表达式）为：

其中，B_k为控制矩阵，u_k为控制变量。

另外，由于控制的不确定性，如车辆打滑，无人机受风吹等原因，预测值及协方差的迭代需要加入噪音影响。

Q_k为加入的噪音，但是为什么不是加在预测变量x_k的计算上，我还没有想明白。

传感器方面（这个方面可以忽略，传感器是不需要转移矩阵的）

上述公式中，H_k表示预测值到传感器读数的转换矩阵。

同理，sensor表示新的协方差矩阵，传感器方面的协方差矩阵。

知识补充：

假定有变量x，通过预测或者观察等方法，发现其服从两个高斯分布，其期望分别是μ_1和μ_2，方差分别是δ_1和δ_2，那么变量真正的分布是多少呢？或者说，根据两个分布，如何推出更接近真实分布的分布？

答案是，两个分布相乘。如上图所示，红色，绿色表示预测或者观察的分布，蓝色则表示两者相乘的分布。至于为何两者相乘更接近真实的分布，则是数学上的事情了。

具体的推导可以见参考文献，这里说一下结论：

两个高斯分布相乘，其新的分布，期望是分布1的期望μ_1加上卡尔曼增益K乘以期望μ_2减去μ_1。K给人的感觉是就是一种权重的计算方法，这个权重就是分布1的方差与分布1+分别2的比值。一种直观的解释是，如果某个测量器（方法）更可靠，则理论上，真值应该更接近这个分布，也就是说，应该给误差更小的分布分配更多的权重。因此，新的分布等于期望μ_1加上卡尔曼增益K乘以期望μ_2减去μ_1，如果分布1更加可靠，则应该更小地调整（更加相信分布1），反之，则应该更大地调整，使得新的分布更加接近分布2。

理解了两个高斯分布，求取其更接近真值的方法就是，两个高斯分布相乘。其核心是卡尔曼增益的计算，即：

分布1的方差占两个和的比例，最后按照这个比例给出最终的高斯分布，或者说更加接近真值的高斯分布。

有了上面的理论基础，我们知道，在卡尔曼滤波中，有两个分布，分别是：

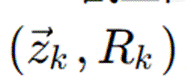
因此，两个分布，利用高斯相乘，可以得到：

简化后有：（我不会，我不知道数学上怎么简化的）

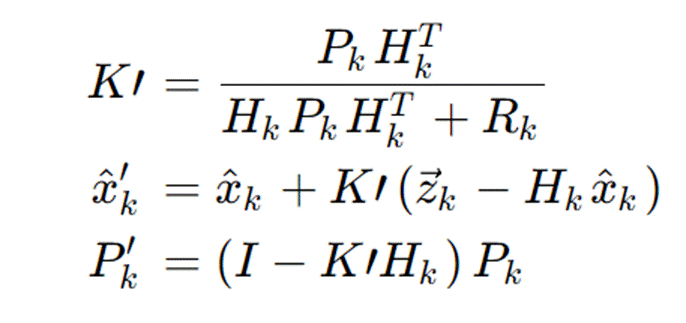
因此，卡尔曼滤波有：

这里，预测是指，给出目标值的预测值。这里包含了预测分别的期望x_k和方差p_k

更新，则是根据传感器的测量分布，更新期望值x_k为x_k^'，使得更加接近真值。同时，更新预测分布的方差P_k^'，使得其下次的预测更加准确。

因此，要实现一个卡尔曼滤波，需要做以下的事情：

1. 给出根据控制量计算出控制目标的控制方程（模型，转移方法），公式

2. 需要给定噪音Q_k的值

3. 传感器测量值的期望和分布

做完上面的事情后，就可以利用卡尔曼滤波来进行优化（使用），使得基于预测模型和传感器测量结果，获得的值更加准确。理论上，经过一定的迭代次数后，预测分布P_k就会稳定到一个值。实际使用中，在P_k收敛后，可以根据预测分布P_k，直接计算出K^'，然后就可以直接计算更加准确的目标值了。这应该也是卡尔曼滤波的一个优势。