当前位置：首页 > news >正文

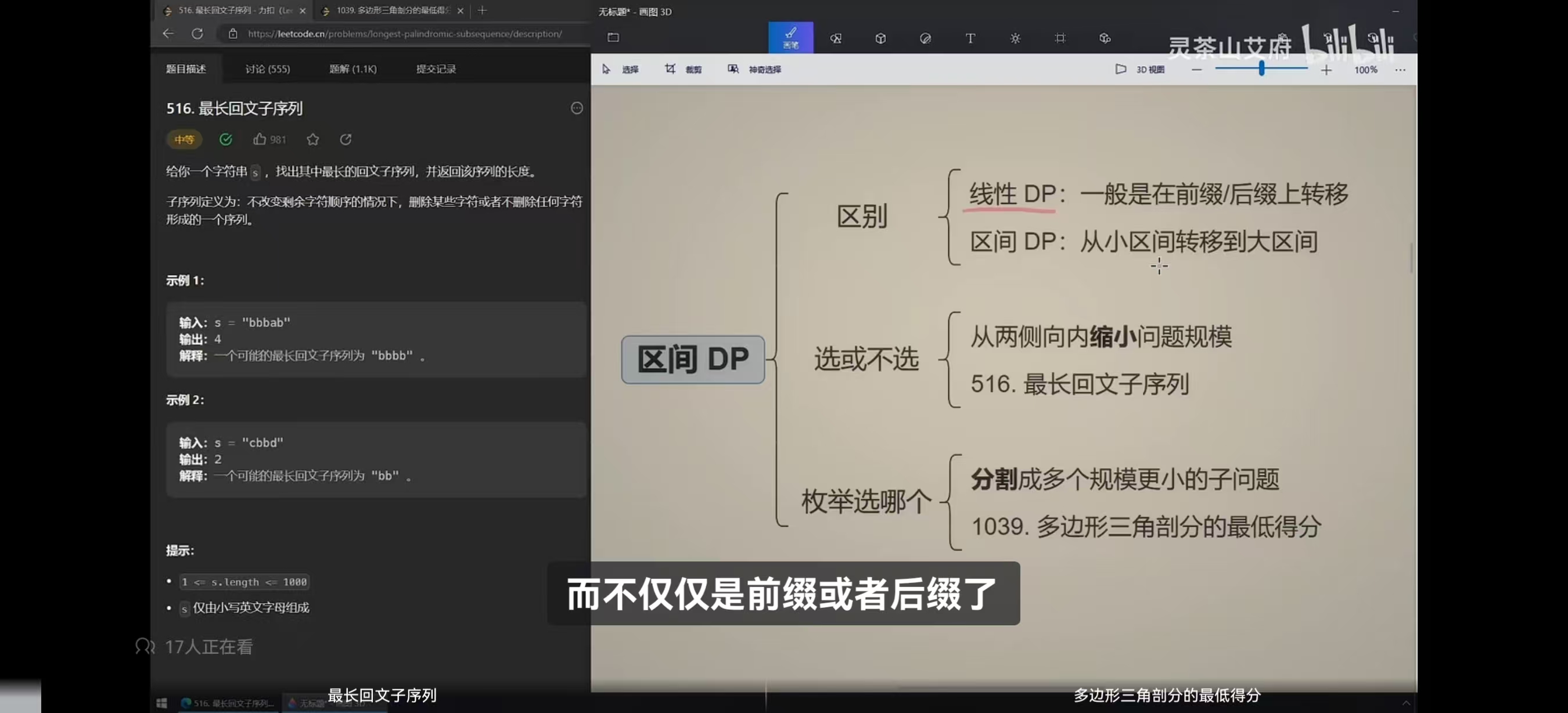
力扣刷题DAY12（动态规划-区间DP）

news 2025/9/8 12:29:57

一、最长回文子序列

516. 最长回文子序列

（一）动态规划

对于一个子序列而言，如果它是回文子序列，并且长度大于 2，那么将它首尾的两个字符去除之后，它仍然是个回文子序列。因此可以用动态规划的方法计算给定字符串的最长回文子序列。

class Solution {
public:
    int longestPalindromeSubseq(string s) {
        int n = s.size();
        vector<vector<int>> f(n, vector<int>(n, 0));
        for (int i = n - 1; i >= 0; i--) {
            f[i][i] = 1;
            for (int j = i + 1; j < n; j++) {
                if (s[i] == s[j])
                    f[i][j] = f[i + 1][j - 1] + 2;
                else
                    f[i][j]=max(f[i+1][j],f[i][j-1]);            
            }
        }
        return f[0][n - 1];
    }
};

复杂度分析

时间复杂度：O(n2)。
空间复杂度：O(n2)。

问：如何思考循环顺序？什么时候要正序，什么时候要倒序？

答：这里有一个通用的做法：盯着状态转移方程，想一想，要计算 f[i][j]，必须先把 f[i+1][⋅] 算出来，那么只有 i 从大到小枚举才能做到。而对于j来说，要计算 f[i][j]，必须先把 f[⋅][j-1] 算出来，那么只有 j 从小到大枚举才能做到。此外，j在i右边，所以在第二层循环的时候，j从i+1开始。

（二）空间优化（滚动数组）

跟最长公共子序列的优化很相似，要保存一些特殊的值传递到下一层循环。

观察到：

状态5的f[j]来自已经更新的f[j-1]和未更新的f[j]，所以f[j] = max(f[j - 1], f[j]);
状态6的f[j]来自未更新的f[j-1]，但是此时f[j-1]已更新，所以需要每次更新f[j]的时候存一下，传到下次j处。
每次刚开始新的一行时，左下角是0，需要特殊初始化一下pre。
每次刚开始新的一行时，第一个数都是1，需要初始化一下f[i]。

class Solution {
public:
    int longestPalindromeSubseq(string s) {
        int n = s.size();
        vector<int> f(n, 0);
        for (int i = n - 1; i >= 0; i--) {
            int pre = 0; // 每一行新开始的时候，左下角都是0
            f[i] = 1;
            for (int j = i + 1; j < n; j++) {
                int temp = f[j]; // 记录此时的f[j]，以便成为左下角
                if (s[i] == s[j])
                    f[j] = pre + 2;
                else
                    f[j] = max(f[j - 1], f[j]);
                pre = temp; // 保存下一个j的左下角
            }
        }
        return f[n - 1];
    }
};

复杂度分析

时间复杂度：O(n2)。
空间复杂度：O(n)。

（三）倒序 + 最长公共子序列

回文子序列本质就是：该字符串与自己的逆序串求最长公共子序列。

class Solution {
public:
    int longestPalindromeSubseq(string s) {
        string rs = s;
        reverse(rs.begin(), rs.end());
        int n = s.size();
        vector<vector<int>> f(n + 1, vector<int>(n + 1, 0));
        for (int i = 1; i <= n; i++) {
            for (int j = 1; j <= n; j++) {
                if (s[i - 1] == rs[j - 1])
                    f[i][j] = f[i - 1][j - 1] + 1;
                else
                    f[i][j] = max(f[i - 1][j], f[i][j - 1]);
            }
        }
        return f[n][n];
    }
};

复杂度分析

时间复杂度：O(n2)。
空间复杂度：O(n2)。

二、最长回文子串

5. 最长回文子串

class Solution {
public:
    string longestPalindrome(string s) {
        int n = s.size();
        vector<vector<bool>> f(n, vector<bool>(n, false));
        int max = 1;
        int start = 0;
        for (int i = 0; i < n; i++)
            f[i][i] = true;
        for (int j = 1; j < n; j++) {
            for (int i = 0; i < n-1 && i < j; i++) {
                if (s[i] != s[j])
                    f[i][j] = false;
                else {
                    if (j - i < 3)
                        f[i][j] = true;
                    else
                        f[i][j] = f[i + 1][j - 1];
                }
                if (f[i][j] && j - i + 1 > max) {
                    max = j - i + 1;
                    start = i;
                }
            }
        }
        return s.substr(start, max);
    }
};

复杂度分析